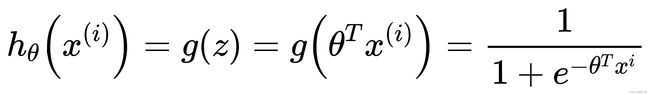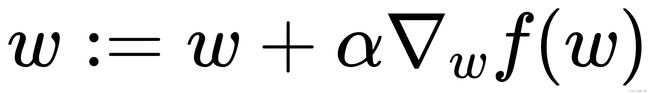Logistic回归-机器学习

一、logistics回归是什么

Logistic回归是统计学习中的经典分类方法，属于对数线性模型，所以也被称为对数几率回归。虽然是叫做回归，但其实这是一种分类算法，Logistic回归是一种线性分类器，针对的是线性可分问题。利用logistic回归进行分类的主要思想是：根据现有的数据对分类边界线建立回归公式，以此进行分类。

二、Sigmoid激活函数

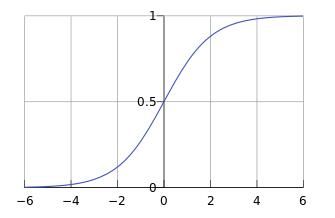
sigmoid函数是一个s形曲线，就像是阶跃函数的温和版，阶跃函数在0和1之间是突然的起跳，而sigmoid有个平滑的过渡。

在进行分类的时候 可以使用一个函数对数据集进行分类 可对比线性回归函数 在分界线上的为一类 在分界线下方的为一类

                

（这里θT是一个向量)

其中 i=1,2,...m，表示第 i个样本, n 表示特征数,当 z(x(i))>0 时，对应着样本点位于分界线上方，可将其分为"1"类；当 z(x(i))<0 时 ，样本点位于分界线下方，将其分为“0”类。

逻辑回归作为分类算法，它的输出是0/1。那么如何将输出值转换成0/1呢？

这就需要一个新的函数——sigmoid 函数

将z(x(i))z(x^{(i)})z(x(i))的结果值映射到sigmod函数上可以得到对应的概率值

带入后逻辑回归模型函数变成

 三、梯度上升法

梯度上升法基于的思想是：要找到某函数的 最大值，最好的方法是沿着该函数的梯度方向探寻。如果梯度记为∇，则函数f(x,y)的梯度由 下式表示：

                                                           

这个梯度意味着要沿x的方向移动 ，沿y的方向移动 。其中，函数f(x,y) 必须要在待计算的点上有定义并且可微。如下图：

 

上图展示的，梯度上升算法到达每个点后都会重新估计移动的方向。从 P0 开始，计算完该点的梯度，函数就根据梯度移动到下一点 P1。在 P1 点，梯度再次被重新计算，并沿着新的梯度方向移动到 P2 。如此循环迭代，直到满足停止条件。迭代过程中，梯度算子总是保证我们能选取到最佳的移动方向。

上图中的梯度上升算法沿梯度方向移动了一步。可以看到，梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向，而未提到移动量的大小。该量值称为步长，记作 α 。用向量来表示的话，梯度上升算法的迭代公式如下:

 

该公式将一直被迭代执行，直至达到某个停止条件为止，比如迭代次数达到某个指定值或者算法达到某个可以允许的误差范围。

四、代码实现

        准备数据集

上表数据是对LOL玩家更喜爱玩的模式的数据统计，取近十把游戏记录的使用英雄数和平均对局时长。

将上表的数据存储到dataSet.txt文件中，最后一列的0,1分别代表更喜欢玩大乱斗模式和排位模式。

加载数据

def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open('dataSet.txt')
    for line in fr.readlines():                                       # 遍历读取数据
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat

绘制数据

# 绘制数据集
def showData():
    dataMat, labelMat = loadDataSet()
    dataArr = ny.array(dataMat)
    n = ny.shape(dataArr)[0]
    xcord1 = []; ycord1 = []                               # 存放正样本
    xcord2 = []; ycord2 = []                               # 存放负样本
    for i in range(n):                                     # 依据数据集的标签来对数据进行分类
        if int(labelMat[i]) == 1:                          # 标签为1，为正样本
            xcord1.append(dataArr[i, 1]); ycord1.append(dataArr[i, 2])
        else:
            xcord2.append(dataArr[i, 1]); ycord2.append(dataArr[i, 2])
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
    plt.rcParams['axes.unicode_minus'] = False
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=15, c='blue')
    ax.scatter(xcord2, ycord2, s=15, c='red', marker='s')
    plt.title('LOL更偏爱模式分类结果')  # 标题
    plt.xlabel('英雄数')
    plt.ylabel('对局时长')  # x，y轴的标签
    plt.show()

        sigmoid函数

def sigmoid(inX):
    return 1.0 / (1 + ny.exp(-inX))

        梯度上升算法

def gradAscent(dataMatIn, classLabels):                            
    dataMatrix = ny.mat(dataMatIn)                                    # 转换为NumPy矩阵
    labelMat = ny.mat(classLabels).transpose()                        # 转换为NumPy矩阵，并且矩阵转置
    m, n = ny.shape(dataMatrix)                                       # 获取数据集矩阵的大小，m为行数，n为列数
    alpha = 0.01                                                  # 目标移动的步长
    maxCycles = 500                                                # 迭代次数
    weights = ny.ones((n, 1))                                         # 权重初始为1
    for k in range(maxCycles):                                     # 重复矩阵运算
        h = sigmoid(dataMatrix * weights)                          # 矩阵相乘，计算sigmoid函数
        error = (labelMat - h)                                     # 计算误差
        weights = weights + alpha * dataMatrix.transpose() * error # 矩阵相乘，更新权重
    return weights

计算出回归系数

 

 完整代码

from matplotlib import pyplot as plt
import numpy as ny

def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open('dataSet.txt')
    for line in fr.readlines():                                       # 遍历读取数据
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat

# sigmoid函数
def sigmoid(inX):
    return 1.0 / (1 + ny.exp(-inX))

# 梯度上升算法
def gradAscent(dataMatIn, classLabels):
    dataMatrix = ny.mat(dataMatIn)                                    # 转换为NumPy矩阵
    labelMat = ny.mat(classLabels).transpose()                        # 转换为NumPy矩阵，并且矩阵转置
    m, n = ny.shape(dataMatrix)                                       # 获取数据集矩阵的大小，m为行数，n为列数
    alpha = 0.01                                                  # 目标移动的步长
    maxCycles = 500                                                # 迭代次数
    weights = ny.ones((n, 1))                                         # 权重初始化为1
    for k in range(maxCycles):                                     # 重复矩阵运算
        h = sigmoid(dataMatrix * weights)                          # 矩阵相乘，计算sigmoid函数
        error = (labelMat - h)                                     # 计算误差
        weights = weights + alpha * dataMatrix.transpose() * error # 矩阵相乘，更新权重
    return weights


# 绘制数据集和Logistic回归最佳拟合直线
def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()                      
    dataArr = ny.array(dataMat)                               # 转换成umPy的数组
    n = ny.shape(dataArr)[0]                                  
    xcord1 = []; ycord1 = []                               # 存放正样本
    xcord2 = []; ycord2 = []                               # 存放负样本
    for i in range(n):                                     
        if int(labelMat[i]) == 1:                          # 数据的标签为1，表示为正样本
            xcord1.append(dataArr[i, 1]); ycord1.append(dataArr[i, 2])
        else:                                              
            xcord2.append(dataArr[i, 1]); ycord2.append(dataArr[i, 2])
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=20, c='blue', marker='s')  # 绘制正样本
    ax.scatter(xcord2, ycord2, s=20, c='red')            # 绘制负样本
    x = ny.arange(1.0, 10.0, 0.01)                             # x区间
    y = (-weights[0] - weights[1] * x) / weights[2]        # 最佳拟合直线
    ax.plot(x, y)
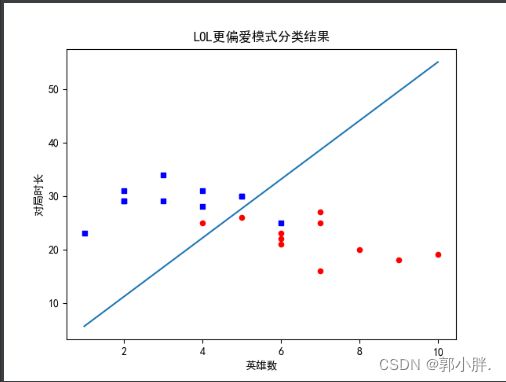
    plt.title('LOL更偏爱模式分类结果')                                   # 标题
    plt.xlabel('英雄数'); plt.ylabel('对局时长')                     # x，y轴的标签
    plt.show()

# 运行画出图
dataMat, labelMat = loadDataSet()
weigths = gradAscent(dataMat, labelMat)
plotBestFit(weigths.getA())
print("w0: %f, w1: %f, W2: %f" % (weigths[0], weigths[1], weigths[2]))

 运行结果