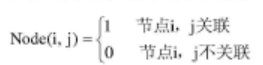配电网重构知识及matlab实现（2）

 

上一篇配电网重构文章解决了如何利用基本环方法实现配电网重构，解决了智能算法求解配电网重构的断开线路组合难题，大大提高了重构运算效率，但是对于环网检测和孤岛判断并没有深入分析，这篇文章主要通过配电网分层方法、环岛检测和孤岛判断进一步深入分析。

一、分层方法和孤岛、环网检测

首先根据支路参数矩阵很方便求取节点关联矩阵，假设配电网节点数量为N，那么该节点关联矩阵维度为N*N，定义该节点中元素值：

通过节点关联矩阵，很容易复原一个配电网络的拓扑结构，在这里可以采用两个矩阵来分层确定网络状态，设节点分层矩阵为LN，上层节点矩阵为UN。

分层矩阵LN就是按照从平衡节点到末梢节点的顺序逐步确定配电网络层次结构，UN矩阵为1*N的矩阵，是每个节点上层节点信息。

具体详细实例可以参见文章《分布式电源优化配置与配电网重构》（关万琳），同时实例更能清楚掌握配电网分层步骤和理论方法。

将一个配电网络从初始节点至末梢节点逐步分层后，就得到了每个节点对应的上层节点，也就是上层节点矩阵UN。

当上层节点矩阵UN除平衡节点外，其余节点对应的上层节点均不为0，一般来说，UN矩阵除第一个元素为0外，其余元素均不为0就说明没有形成孤岛，只要有一个元素为0就说明网络是存在孤岛的，这就是孤岛检测方法。

以33节点为例，假设利用基本环方法得到的配网系统断开线路变量Swarm=[4,12,9,7,26]（这个变量之前被留言私信询问多次）,则得到网络节点关联矩阵为：

上层节点矩阵为：

 因为UN矩阵中第567列元素为0，所以可以得到该网络存在孤岛，也就是存在不可行解，在智能算法计算中可以通过罚函数的形式避免此类问题出现。

结合上一篇所讲，环网检测方法即通过判定断开开关不存在重复线路，也就是每个环网断开不同的开关，配电网就不存在环网。

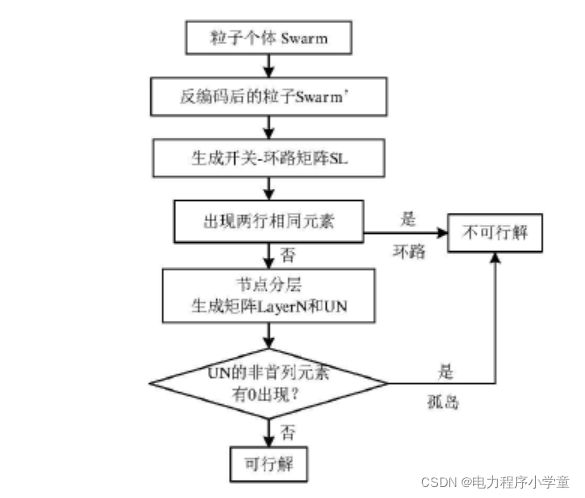
二、不可行解判断步骤

 三、matlab程序实例

%该为智能算法程序计算子函数，加入不可行解判断程序（在指定节点处加入DG）
b=32;
k=1; 
n=33;
LL=5;           %联络开关数  z
Sb=10;          %MW
Vb=12.66;       %KV
Zb=Vb^2/Sb;     %ohm
check=1;
checkhl=1;
checkgd=1;
H=[ 2	3	4	5	6	7	33	20	19	18	0	0	0	0	0	0	0	0	0	0	0
    9	10	11	12	13	14	34	0	0	0	0	0	0	0	0	0	0	0	0	0	0
    2	3	4	5	6	7	8	9	10	11	35	21	20	19	18	0	0	0	0	0	0
    6	7	8	9	10	11	12	13	14	15	16	17	36	32	31	30	29	28	27	26	25
    3	4	5	25	26	27	28	37	24	23	22	0	0	0	0	0	0	0	0	0	0];%由函数matrixH生成
     for i1=1:LL
        a(1,i1)=H(i1,Swarm1(1,i1));
    end
%  NodeM(:,2)=NodeM(:,2)+SDG; 
%1、判断是否形成环路，F为支路环路关联矩阵(行表示回路，列表示断开开关，若任意两行相同，则表示形成了环路)   
F=zeros(5);
for i1=1:LL  %回路
    for i2=1:LL   %断开开关
        if max(a(1,i2)==H(i1,:))
            F(i1,i2)=1;
        end
    end
end
for i1=1:LL-1
    for i2=i1+1:LL
        if min(F(:,i1)==F(:,i2))
        checkhl=0;                %disp('出现环路')%出现环路时
        guan=10000;
        end
    end
end
for i1=1:LL          %按照断开开关矩阵，剔除Z矩阵中的断开支路
    j=i1-1;
    for i2=1:b+LL-j
        if BranchM(i2,1)==a(1,i1)
            BranchM(i2,:)=[];
            break
        end
    end
end
NodeN=zeros(n);   %节点-节点关联矩阵A
for i1=1:b
    NodeN(BranchM(i1,2),BranchM(i1,3))=1;
    NodeN(BranchM(i1,3),BranchM(i1,2))=1;
end
 
LayerM=[1];      %节点分层矩阵，电源节点号记“1”
NU=zeros(1,n);   %上层节点矩阵（有33列的行矩阵）
 while(checkhl==1)
 
 
 
%以下用循环求取矩阵LayerM和NU
 
while(checkgd==1)
    h=1;
while(min(NU(2:33)~=0)==0) %NU矩阵的2-最后都有上层节点了，表示循环结束了
m=max(find(LayerM(:,h)));  %m为矩阵LayerM第h列非零元素的个数
 k=1;
for i1=1:m     
    g=LayerM(i1,h);           %LayerM的第i1行第h列元素
    ss=find(NodeN(g,:)==1);
       for i2=1:length(ss)
        if LayerM~=ss(1,i2)   %排除相同节点
           LayerM(k,h+1)=ss(1,i2);
           NU(1,ss(1,i2))=g;
           k=k+1;             %k表示第h层含有的节点数
        end
       end
end
h=h+1;                     %h表示网络分层的层数
if length(LayerM(1,:))==h-1  %如果网络分层矩阵没有搜索到下层节点，说明形成了断点，后边网络形成了孤岛，与电源节点没有连通回路
        checkgd=0;        
        %disp('形成孤岛')
        guan=10000;
        check=0;
        break       %结束循环
    end
end
if min(NU(2:33)~=0)  %若解可行，已经计算完LayerM，则让其跳出最外层while循环
    checkgd=0;
    %disp('可行解')
  end
end
 
while(check==1)
BranchM(:,4)=BranchM(:,4)/Zb; %阻抗标幺化
NodeM(:,2)=NodeM(:,2)/Sb; %功率标幺化
%下面进行分层前推回代法潮流计算
V=ones(n,1);               %节点电压
J=zeros(n,1);              %支路电流
k=1;                        %记录迭代次数
V0=zeros(n,1);
t=0;
while(max(abs(V-V0))>1e-3) %判断收敛性（收敛精度设为1e-6）
V0=V;                      %记录上一次迭代的电压值
%1、回代求支路电流矩阵J
I=conj(NodeM(:,2)./V);     %节点注入电流
for i1=h:-1:2
    ss=find(LayerM(:,i1)~=0);
    for i2=1:length(ss)
        if min(LayerM(i2,i1)==NU)
            J(LayerM(i2,i1))=I(LayerM(i2,i1));
        else
            sumJ=0;
            gx=find(NU==LayerM(i2,i1));  %求得节点LayerM(i2,i1)的下层节点矩阵（大小不定）
            for i3=1:length(gx)
                sumJ=sumJ+J(gx(1,i3));
            end
            J(LayerM(i2,i1))=I(LayerM(i2,i1))+sumJ;
        end
    end
end
%2、前推求节点电压矩阵V
Z=zeros(n,1);   %支路阻抗
for i1=2:h
    ss=find(LayerM(:,i1)~=0);
    for i2=1:length(ss)
        m1=NU(1,LayerM(i2,i1));       %首节点  
        n1=LayerM(i2,i1);             %尾节点
        for i3=1:b   %从BranchM中搜寻得到各支路阻抗矩阵
            if (BranchM(i3,2)==m1&&BranchM(i3,3)==n1)||(BranchM(i3,2)==n1&&BranchM(i3,3)==m1)
                Z(n1,1)=BranchM(i3,4);
            end
        end
        V(n1,1)=V(m1,1)-Z(n1,1)*J(n1,1);
    end
end
k=k+1;  %迭代次数k
if k>20
   guan=10000;
   break
end
end
%%
Vby=abs(V);
V=V*Vb;         %反标幺
Vm=abs(V);      %节点电压幅值
%————————————————————————————————
%节点电压上下限约束（排除a=[7 9 2 12 3];这种状况）
%if min(Vm)Vb
    %guan=10000;
%end
%————————————————————————————————
Va=angle(V);    %节点电压弧度
%下面计算有功网损fploss
Sloss=zeros(n,1);
Z=zeros(n,1);   %支路阻抗
 
for i1=2:h      %！！！此for循环程序段是为了搜寻网络各支路的首末节点与支路阻抗，应对网络拓扑变化，造成的潮流流向变化
    ss=find(LayerM(:,i1)~=0);
    for i2=1:length(ss)
        m1=NU(1,LayerM(i2,i1));       %首节点  
        n1=LayerM(i2,i1);             %尾节点
        for i3=1:b   %从BranchM中搜寻得到各支路阻抗矩阵
            if (BranchM(i3,2)==m1&&BranchM(i3,3)==n1)||(BranchM(i3,2)==n1&&BranchM(i3,3)==m1)
                Z(n1,1)=BranchM(i3,4);
            end
        end
        Sloss(n1)=(abs(V(m1)-V(n1)))^2/conj(Z(n1,1)*Zb)*1000;  %各支路的功率损耗(单位为kW)
    end
end
Ploss=real(Sloss);   %有功损耗
Qloss=imag(Sloss);   %无功损耗
fPloss=sum(Ploss);   %系统的总有功损耗
guan=fPloss;
check=0;
end
checkhl=0;
 end
if k>20
    guan=10000;
end

 （因篇幅所限，部分参数未展出，即为IEEE33网络节点和支路参数）

完整粒子群算法的重构程序代码链接：

考虑分布式电源的配电网重构优化程序matlab_基于分布式电源的配电网重构优化程序-Matlab文档类资源-CSDN下载配网重构中，很重要的一个约束条件为配网应随时保持开环、辐射的状态：配电网系统是属于闭环设计但是开环基于分布式电源的配电网重构优化程序更多下载资源、学习资料请访问CSDN下载频道.https://download.csdn.net/download/zhangxd212489/73526211