常见聚类算法及使用--层次聚类（Agglomerative clustering）

前言

层次聚类顾名思义就是按照某个层次对样本集进行聚类操作，这里的层次实际上指的就是某种距离定义。
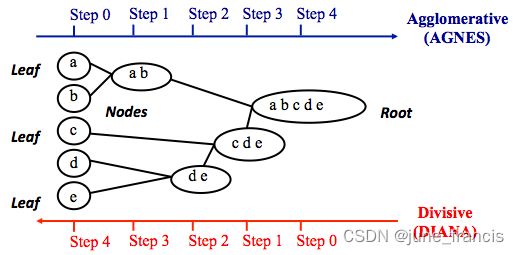
层次聚类最终的目的是消减类别的数量，所以在行为上类似于树状图由叶节点逐步向根节点靠近的过程，这种行为过程又被称为“自底向上”。
更通俗的，层次聚类是将初始化的多个类簇看做树节点，每一步迭代，都是将两两相近的类簇合并成一个新的大类簇，如此反复，直至最终只剩一个类簇（根节点）。
与层次聚类相反的是分裂聚类（divisive clustering），又名 DIANA(Divise Analysis)，它的行为过程为“自顶向下”。
本文重点为大家介绍层次聚类。

层次聚类的实现

聚类过程

• 数据准备；
• 计算数据集中各样本之间的距离（相似度信息）；
• 使用 连接函数（linkage function）将样本进行分组形成层次聚类数（分组依据是上一步计算出来的距离信息），距离相近的样本会被链接在一起；
• 决定在什么地方将层次聚类树截断成多个聚类。

代码实现

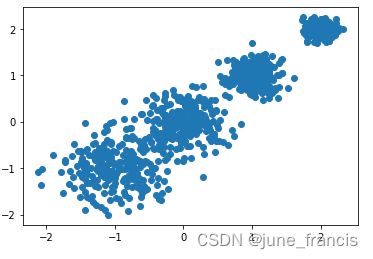
我们先用之前构建的数据来完成一个简单的聚类：

  # 综合分类数据集
  import numpy as np
  from sklearn.datasets import make_blobs
  from matplotlib import pyplot as plt

  # 创建数据集
  # X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共4个簇，
  # 簇中心在[-1,-1], [0,0],[1,1], [2,2]， 簇方差分别为[0.4, 0.2, 0.2, 0.2]
  X, y = make_blobs(n_samples=1000, n_features=2, 
                  centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                  cluster_std=[0.4, 0.3, 0.2, 0.1],
                  random_state=9)
  # 数据可视化
  plt.scatter(X[:, 0], X[:, 1], marker='o')
  plt.show()

然后使用 sklearn.cluster.AgglomerativeClustering 完成聚类：

• 一般参数：

  • n_clusters：一个整数，指定簇的数量。

  • connectivity：一个数组或者可调用对象或者为None，用于指定连接矩阵。它给出了每个样本的可连接样本。

  • affinity：一个字符串或者可调用对象，用于计算距离。可以为：‘euclidean’, ‘l1’, ‘l2’, ‘manhattan’, ‘cosine’, ‘precomputed’ 。
    如果linkage=‘ward’，则 'affinity必须是 ‘euclidean’ 。

  • memory：用于缓存输出的结果，默认为不缓存。如果给定一个字符串，则表示缓存目录的路径。

  • n_components：将在scikit-learn v 0.18中移除

  • compute_full_tree：通常当已经训练了n_clusters之后，训练过程就停止。
    但是如果compute_full_tree=True，则会继续训练从而生成一颗完整的树。

  • linkage：一个字符串，用于指定链接算法。
    ‘ward’：采用方差恶化距离variance incress distance 。
    ‘complete’：全链接complete-linkage算法，采用 $d_{max}$。
    ‘average’：均链接average-linkage算法,采用 $d_{avg}$。
    ‘single’：单链接single-linkage算法，采用 $d_{min}$ 。

  • pooling_func：即将被废弃的接口。

• 属性：

  • labels_：一个形状为[n_samples,] 的数组，给出了每个样本的簇标记。
  • n_leaves_：一个整数，给出了分层树的叶结点数量。
  • n_components_：一个整数，给除了连接图中的连通分量的估计值。
  • children_：一个形状为[n_samples-1,2]数组，给出了每个非叶结点中的子节点数量。

for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
    model = AgglomerativeClustering(
        n_clusters=4, linkage="average", affinity=metric
    )
    model.fit(X)
    print("%s Silhouette Coefficient: %0.3f"
      % (metric, metrics.silhouette_score(X, model.labels_, metric='sqeuclidean')))
    plt.figure()
    plt.axes([0, 0, 1, 1])
    for l, c in zip(np.arange(model.n_clusters), "rgbk"):
        row_ix = np.where(l == model.labels_)
        plt.scatter(X[row_ix, 0], X[row_ix, 1])
    plt.axis("tight")
    plt.axis("off")
    plt.suptitle("AgglomerativeClustering(affinity=%s)" % metric, size=20)

plt.show()

展示结果如下：

cosine Silhouette Coefficient: 0.370
euclidean Silhouette Coefficient: 0.816
cityblock Silhouette Coefficient: 0.820

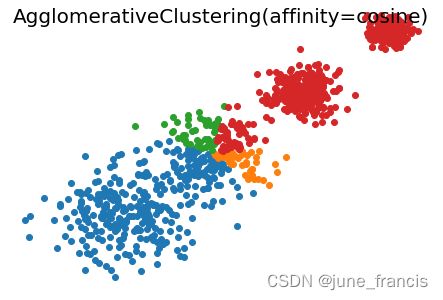
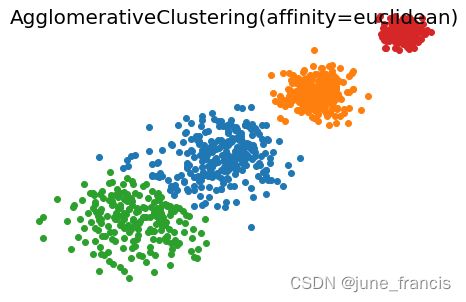
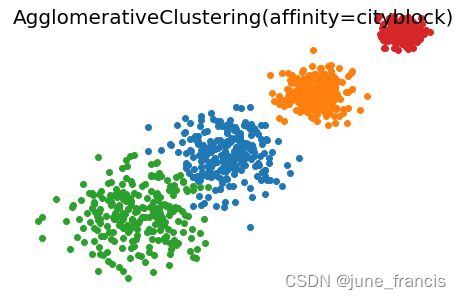
不难看出，当前场景使用 linkage='average' 和 affinity='euclidean' 的参数组合与 linkage='average' 和 affinity='cityblock' 时聚类效果更好。

接下来我们使用更为复杂的数据进行测试（以下示例来自于官方）：

# Author: Gael Varoquaux
# License: BSD 3-Clause or CC-0

import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import AgglomerativeClustering
from sklearn.metrics import pairwise_distances

np.random.seed(0)

# Generate waveform data
n_features = 2000
t = np.pi * np.linspace(0, 1, n_features)


def sqr(x):
    return np.sign(np.cos(x))


X = list()
y = list()
for i, (phi, a) in enumerate([(0.5, 0.15), (0.5, 0.6), (0.3, 0.2)]):
    for _ in range(30):
        phase_noise = 0.01 * np.random.normal()
        amplitude_noise = 0.04 * np.random.normal()
        additional_noise = 1 - 2 * np.random.rand(n_features)
        # Make the noise sparse
        additional_noise[np.abs(additional_noise) < 0.997] = 0

        X.append(
            12
            * (
                (a + amplitude_noise) * (sqr(6 * (t + phi + phase_noise)))
                + additional_noise
            )
        )
        y.append(i)

X = np.array(X)
y = np.array(y)

n_clusters = 3

labels = ("Waveform 1", "Waveform 2", "Waveform 3")

# Plot the ground-truth labelling
plt.figure()
plt.axes([0, 0, 1, 1])
for l, c, n in zip(range(n_clusters), "rgb", labels):
    lines = plt.plot(X[y == l].T, c=c, alpha=0.5)
    lines[0].set_label(n)

plt.legend(loc="best")

plt.axis("tight")
plt.axis("off")
plt.suptitle("Ground truth", size=20)


# Plot the distances
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
    avg_dist = np.zeros((n_clusters, n_clusters))
    plt.figure(figsize=(5, 4.5))
    for i in range(n_clusters):
        for j in range(n_clusters):
            avg_dist[i, j] = pairwise_distances(
                X[y == i], X[y == j], metric=metric
            ).mean()
    avg_dist /= avg_dist.max()
    for i in range(n_clusters):
        for j in range(n_clusters):
            plt.text(
                i,
                j,
                "%5.3f" % avg_dist[i, j],
                verticalalignment="center",
                horizontalalignment="center",
            )

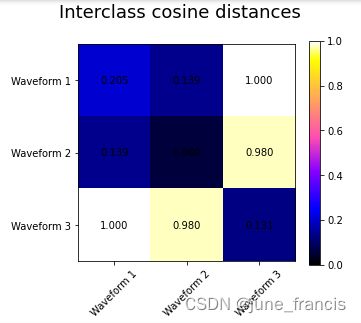
    plt.imshow(avg_dist, interpolation="nearest", cmap=plt.cm.gnuplot2, vmin=0)
    plt.xticks(range(n_clusters), labels, rotation=45)
    plt.yticks(range(n_clusters), labels)
    plt.colorbar()
    plt.suptitle("Interclass %s distances" % metric, size=18)
    plt.tight_layout()


# Plot clustering results
for index, metric in enumerate(["cosine", "euclidean", "cityblock"]):
    model = AgglomerativeClustering(
        n_clusters=n_clusters, linkage="average", affinity=metric
    )
    model.fit(X)
    plt.figure()
    plt.axes([0, 0, 1, 1])
    for l, c in zip(np.arange(model.n_clusters), "rgbk"):
        plt.plot(X[model.labels_ == l].T, c=c, alpha=0.5)
    plt.axis("tight")
    plt.axis("off")
    plt.suptitle("AgglomerativeClustering(affinity=%s)" % metric, size=20)

plt.show()

展示效果如下：







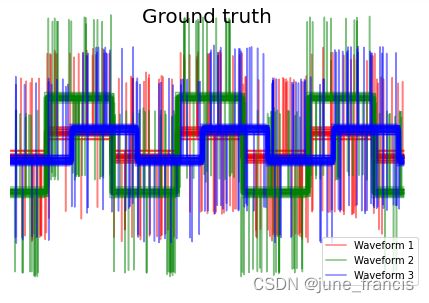
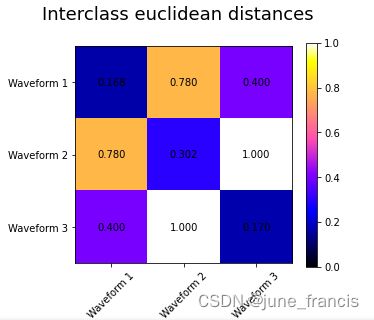
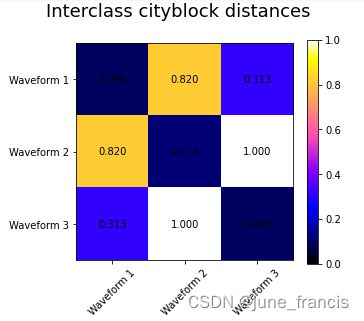
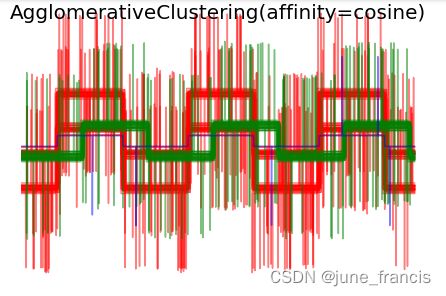
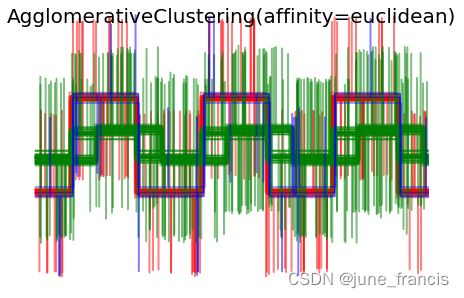
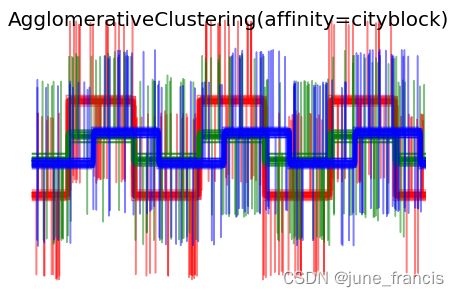
为了演示不同的距离计算方式对层次聚类结果的影响，官方示例中特意构建了波形样本集，这样的样本集可被看作高维的向量，当然了，官方提供的这些距离计算方式也通常用在高维数据场景下（特别是欧氏距离 euclidean 和曼哈顿距离 cityblock ）。

示例中构建的波形数据一共有三组，第一组和第二组实际上其中一组是由另一组等比缩放得到的。而余弦距离 cosine distance 对于缩放前后的数据进行处理得到的结果是一样的，所以，它无法区分这两组波形数据，对于没有噪声的缩放数据，余弦距离同样无法分辨。

在这些波形数据中被加入了观测噪声，这些噪声都是比较稀疏的，仅有 6% 的数据包含噪声，所以，L1范数（例如 cityblock 距离）的噪声要比 L2范数（例如 euclidean 距离）的噪声要大很多。这些都能从上面的类内距离矩阵中看出来：在对角线上的数值，表明了类的分布的广度。

当我们对这些数据进行聚类时，聚类的效果反映在了距离矩阵中。在应用了欧式距离方法的类中，由于噪声的原因样本被聚类的不是很好，所以这种方式无法很好的区分这些波形样本。而对于曼哈顿距离，所有的波形数据都被很好的区分出来。然而余弦距离则无法区分波形数据1和波形数据2，应为它俩被分为了同一个类簇。

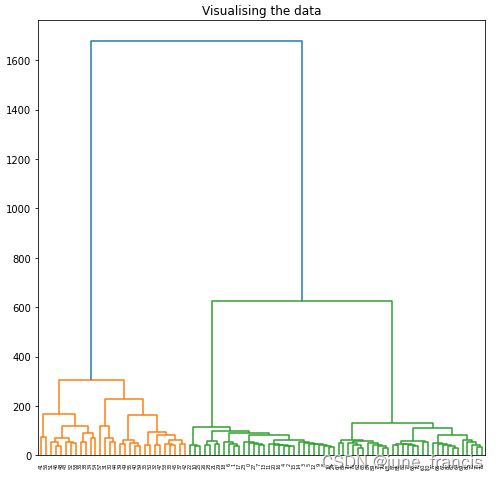
将上述构建的数据进行层次的可视化：

import scipy.cluster.hierarchy as shc

plt.figure(figsize =(8, 8))
plt.title('Visualising the data')
Dendrogram = shc.dendrogram((shc.linkage(X, method ='ward')))

展示效果如下：

参考文献

1. https://scikit-learn.org/stable/auto_examples/cluster/plot_agglomerative_clustering_metrics.html#sphx-glr-auto-examples-cluster-plot-agglomerative-clustering-metrics-py
2. https://www.datanovia.com/en/lessons/agglomerative-hierarchical-clustering/
3. https://www.geeksforgeeks.org/implementing-agglomerative-clustering-using-sklearn/