西瓜书课后题——第九章(聚类)
本章因为课后题大部分都是证明和解答题,所以不再详细叙述,只是针对 9.4 题给出相关算法的实现。
关于证明和简答题可以参考这篇博客: https://blog.csdn.net/icefire_tyh/article/details/52224676
9.4 k均值聚类实现,并在不同k值和初始向量情况下进行比较。
算法完全按照图 9.2 给出的过程进行,数据集采用西瓜数据集4.0.
相关代码如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
class Cluster:
def loadData(self): # 读入数据
dataset = pd.read_excel('./WaterMelon_4.0.xlsx',encoding = 'gbk') # 读取数据
Attributes = dataset.columns # 所有属性的名称
m,n = np.shape(dataset) # 得到数据集大小
dataset = np.matrix(dataset)
for i in range(m): # 将标签替换成 好瓜 1 和 坏瓜 -1
if dataset[i,n-1]=='是': dataset[i,n-1] = 1
else : dataset[i,n-1] = -1
self.future = Attributes[1:n-1] # 特征名称(属性名称)
self.x = dataset[:,1:n-1] # 样本
self.y = dataset[:,n-1].flat # 实际标签
self.m = m # 样本个数
# 执行聚类过程
def cluster(self,k,U): # U是初始均值向量,k为聚类数
C = {}
d = np.ones((k,))
for i in range(self.m):
for j in range(k):
d[j] = self.distance(U[j,:],self.x[i,:]) # 计算每一个均值向量到 xi 的距离
lamda = np.argmin(d)
if (lamda+1) in C:
C[lamda+1] = np.vstack((C[lamda+1],self.x[i,:]))
else:
C[lamda+1] = self.x[i,:]
return C
# 计算距离函数
def distance(self,p,q):
p = np.array(p)
q = np.array(q)
return np.linalg.norm(q-p)
# 更新均值向量
def getNewMean(self,W,U):
flag = 0
means = list()
keys = W.keys()
for key in keys:
X = W[key]
u = np.mean(X,0)
if u==U:
continue
else:
means.append(u)
flag = 1
return means,flag # flag为1说明进行了更新
# 迭代执行整个聚类更新过程
def train(self,k,U):
flag = 1
count = 1
while (flag == 1 & count <= 15):
C = self.cluster(k,U)
print(np.shape(C[1]))
means,flag = self.getNewMean(C,U)
U = means
count = count + 1
return C,U
# 绘制分类结果图
def myplot(self,C,U):
keys = C.keys()
for key in keys:
x1 = C[key][:,0]
x2 = C[key][:,1]
#print(C[key][1])
#hull = cv2.convexHull(C[key])
plt.plot(x1,x2,'.')
#plt.plot(hull[:,0,0],hull[:,0,1],'g-.')
U = np.array(U)
print(U[0,0])
plt.plot(U[:,:,0],U[:,:,1],'+')
plt.xlabel('密度')
plt.ylabel('含糖率')
plt.show()
# 聚类
def myTest(self,k,index): # k为聚类的数量,index为初始的均值向量的索引
self.loadData()
#space = np.floor(self.m/k)
#index = [int(np.random.uniform(i*space,i*space+space)) for i in range(k)]
U = list()
for i in index:
U.append(self.x[i,:])
C,U = self.train(k,np.array(U))
self.myplot(C,U)
def main():
clust = Cluster()
clust.myTest(2,[6,15]) # 两类
clust.myTest(3,[5,15,25]) # 三类
clust.myTest(4,[5,15,20,25]) # 四类
if __name__ == '__main__':
main()
最终的分类结果:
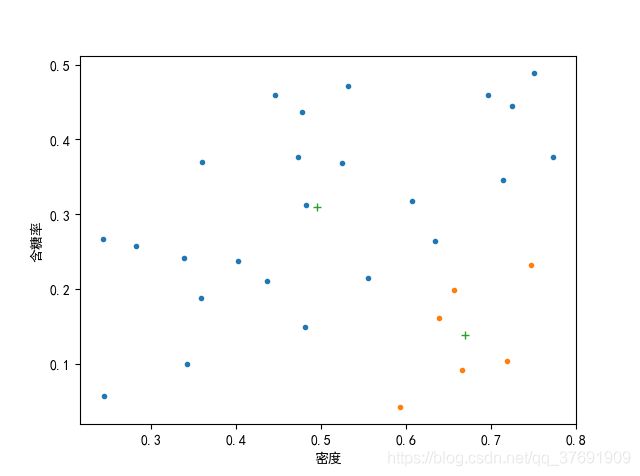
当k=2时:
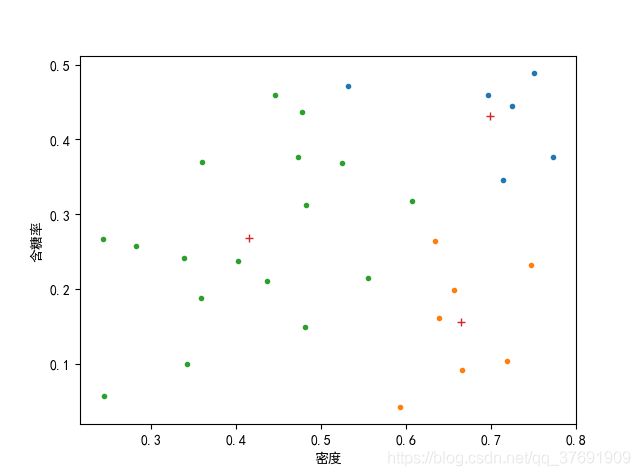
当k=3时:
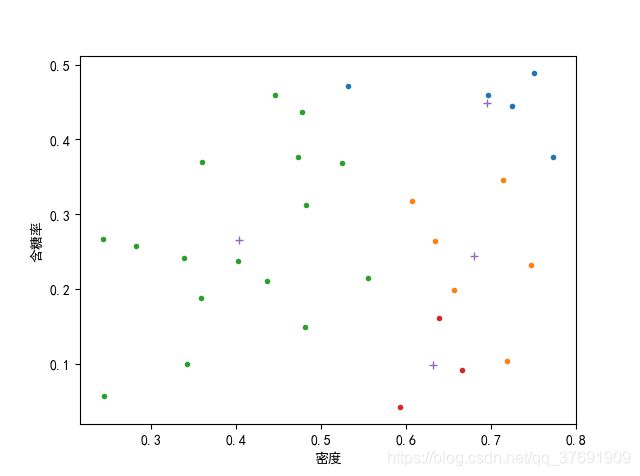
当k=4时:
在试验过程中,最初的想法是随机选取初始值,但是发现随机选取的结果很不稳定,初始向量对最终的影响很大。所以此处是人为指定了初始向量。
总而言之,初始向量的选择对结果有很大影响,因尽量选择处于类中心的点,可能结果比较好,而且收敛很快。
还有一点不足是在绘图时,不知道如何绘制出书上的那种带有类与类之间边界的虚线, 所以结果看起来不完美,如果哪位知道还请不吝赐教!!!
9.10 设计一个可以自动确定聚类类别数的k均值算法。
请参考这篇文章:https://blog.csdn.net/icefire_tyh/article/details/52224612
其思想是在每一个k值聚类完成后,计算所有类中每一个样本距均值向量的距离,然后求和。 之后再计算出整个系统的熵,使这两项的和达到最小,则对应的 k 即是最佳的分类数。
前者的距离之和是为了保证类内的样本比较集中;后者的熵是为了保证类别数目不能过多。 为达到两者之间的权衡,所以权衡的系数设置也比较重要,应该根据数据实际情况进行确定。