MAML: meta learning 论文分析
https://zhuanlan.zhihu.com/p/57864886
一、Meta-Learning 简述
Meta-Learning(即元学习)是最近比较火的研究方向,其思想是learning to learn(学会学习)。Meta-Learning面向的不是学习的结果,而是学习的过程。其学习不是一个直接用来预测的数学模型,而是学习“如何更快更好地学习一个数学模型”。Meta-Learning常用来解决少量样本的Few-shot Learning问题,其目标是针对各种学习任务训练模型,以便仅使用少量训练样本即可解决新的学习任务。 本次报告主要介绍Meta-Learning领域的一篇2017年发表在JMLR的期刊论文:Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks(简称MAML),属于CCF A区。本次报告任务是解读该论文的算法和跑论文提供的开源代码并对代码和结果分析,说明算法的性能。
- MAML算法分析
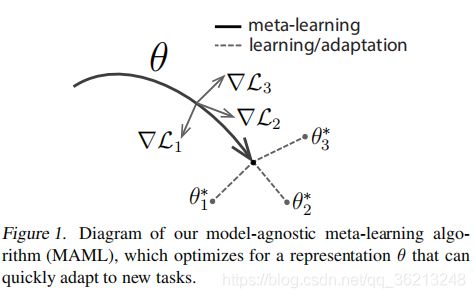
图1 MAML学习过程
如图1所示。MAML的目标是找到对任务(task)的变化敏感的模型参数(model parameters),这样,当损失梯度(loss gradient)的方向改变时,参数的微小变化将对从所有任务分布p(T)提取的任何一个任务(task)的损失函数(loss function)产生较大的改善。即可以使用新任务(new task)上少量的样本fine tune模型后得到新的模型参数(model parameters, θ)对新任务检测的性能有很大的提升。
图2 MAML 算法步骤
如图2所示是MAML算法。该算法实质是MAML训练阶段的算法,目的是得到模型Mmeta。以下是该算法的分析:
首先对于1、2行的两个Require的说明。第一个Require的p(T)指的是meta-train中tasks的分布;第二个Require中的α和β指的是步长(step size),也可以理解为学习率(learning rate).MAML的模型训练过程是gradient by gradient,即MAML是基于二级梯度的,每次迭代包含两次的参数更新的过程,分别对应两个学习率α和β。
步骤1:随机初始化模型的参数。
步骤2:是一个外循坏。每次迭代可以理解为一个epoch,每个epoch训练多个任务中的若干个任务。预训练过程有多个任务,也就对应多个epoch。
步骤3:随机对若干个(meta size)任务进行采样,形成一个meta batch训练数据。
步骤4:这是一个内循环。利用meta batch中的每一个任务Ti,分别对模型的参数进行更新(比如4个任务更新4次参数)。
步骤5:在N-way K-shot(N-way指训练数据中有N个类别class,K-shot指每个类别下有K个被标记数据)的设置下,利用meta batch中的某个task中的support set(任务中少量中有标签的数据,可以理解为训练集training set)的N*K个样本计算每个参数的梯度。
步骤6:第一次梯度的更新的过程。针对Meta batch的每个任务Ti更新一次参数得到新的模型参数θi,这些新模型参数会被临时保存,用来接下的第二次梯度计算,但其并不是真正用来更来更新模型。
步骤7:内循环结束。
步骤8:第二次梯度更新的过程。这个是计算一个query set (另一部分有标签的数据,可以理解为验证集validation set,用来验证模型的泛化能力) 中的5-way*V (V是一个变量,一般等于K,也可以自定义为其他参数比如15)个样本的损失loss,然后更新meta模型的参数,这次模型参数更新是一个真正的更新,更新后的模型参数在该次meta batch结束后回到步骤3用来进行下一次mata batch的计算。
步骤8:外循环结束。
算法后续补充:上面是meta模型训练阶段的算法,对于测试阶段的补充如下:
首先,利用上面训练好的模型Mmeta初始化参数,这个和fine tune的随机初始化不同其中一个不同之处。然后,随机抽取测试集test set中若干(e.g. 500)个task中的少量样本分别微调(可以更新模型一次或者多次)模型Mmeta,接着这些task剩余的数据进行测试得到Accuracy和Loss。最后对测试结果进行求平均,从而避免极端情况。
- MAML关键代码分析(maml.py,红色注释为代码分析,代码是tensorflow实现)
class MAML: # MAML类
def __init__(self, dim_input=1, dim_output=1, test_num_updates=5): # 初始化方法
""" must call construct_model() after initializing MAML! """
self.dim_input = dim_input # 输入维度
self.dim_output = dim_output # 输出维度
self.update_lr = FLAGS.update_lr # 内循环模型参数学习率
self.meta_lr = tf.placeholder_with_default(FLAGS.meta_lr, ()) # 外循环模型学习率
self.classification = False # 是否为分类任务的标记
self.test_num_updates = test_num_updates # 模型验证时参数更新的次数
if FLAGS.datasource == 'sinusoid': # sinusoid 回归任务部分
self.dim_hidden = [40, 40] # 隐含层的节点个数
self.loss_func = mse # mse损失函数
self.forward = self.forward_fc # 模型前向传播函数,输入数据后得到输出
self.construct_weights = self.construct_fc_weights # 构造模型的权值
elif FLAGS.datasource == 'omniglot' or FLAGS.datasource == 'miniimagenet':
# 分类任务,针对两个不同的数据集,模型的前向传播函数和权值构造会有所不同
self.loss_func = xent # 交叉熵损失函数
self.classification = True # 是分类任务
if FLAGS.conv: # 如果模型具有卷积层
self.dim_hidden = FLAGS.num_filters
self.forward = self.forward_conv
self.construct_weights = self.construct_conv_weights
else: # 否则为全连接层网络结构
self.dim_hidden = [256, 128, 64, 64]
self.forward=self.forward_fc
self.construct_weights = self.construct_fc_weights
if FLAGS.datasource == 'miniimagenet':
self.channels = 3 # miniimagenet数据集的通道数为3
else:
self.channels = 1 #omniglot数据集的通道数为1
self.img_size = int(np.sqrt(self.dim_input/self.channels)) # 图片的尺寸
else:
raise ValueError('Unrecognized data source.')
def construct_model(self, input_tensors=None, prefix='metatrain_'): # 模型构造方法
# a: training data for inner gradient, b: test data for meta gradient
if input_tensors is None:
self.inputa = tf.placeholder(tf.float32) # 内层梯度计算的训练数据
self.inputb = tf.placeholder(tf.float32) # 内层梯度计算的训练数据的标签
self.labela = tf.placeholder(tf.float32) # 外层梯度计算的验证数据
self.labelb = tf.placeholder(tf.float32) # 外层梯度计算的验证数据的标签
else:
self.inputa = input_tensors['inputa']
self.inputb = input_tensors['inputb']
self.labela = input_tensors['labela']
self.labelb = input_tensors['labelb']
with tf.variable_scope('model', reuse=None) as training_scope:
if 'weights' in dir(self):
training_scope.reuse_variables()
weights = self.weights
else:
# Define the weights
self.weights = weights = self.construct_weights()
# outputbs[i] 和 lossesb[i] 是第i+1次梯度更新后的模型output和loss
lossesa, outputas, lossesb, outputbs = [], [], [], [] # 损失和输出变量
accuraciesa, accuraciesb = [], [] # 准确率变量
num_updates = max(self.test_num_updates, FLAGS.num_updates)
# meta 任务时的更新次数
outputbs = [[]]*num_updates
lossesb = [[]]*num_updates
accuraciesb = [[]]*num_updates
def task_metalearn(inp, reuse=True): # meta 学习任务方法,算法对应的核心
""" Perform gradient descent for one task in the meta-batch. """
inputa, inputb, labela, labelb = inp
task_outputbs, task_lossesb = [], []
if self.classification:
task_accuraciesb = []
task_outputa = self.forward(inputa, weights, reuse=reuse) # 计算模型输出
# only reuse on the first iter,只有在第一次迭代重用模型权值
task_lossa = self.loss_func(task_outputa, labela) # 计算内循环模型损失
grads = tf.gradients(task_lossa, list(weights.values())) # 内循环梯度计算
if FLAGS.stop_grad: # 反传进行截断
grads = [tf.stop_gradient(grad) for grad in grads]
gradients = dict(zip(weights.keys(), grads)) # 梯度转换为key-value形式
fast_weights = dict(zip(weights.keys(), [weights[key]-self.update_lr*gradients[key] for key in weights.keys()])) # 计算临时更新后模型的新权值
output = self.forward(inputb, fast_weights, reuse=True)
# 使用临时的新权值和验证数据计算模型输出
task_outputbs.append(output) # 临时保存输出,用于外循环损失计算
task_lossesb.append(self.loss_func(output, labelb))
# 临时保存损失,用于外循环梯度计算
for j in range(num_updates - 1):
# 前面临时更新了一次,所以剩下num_updates - 1次
# 迭代meta 任务的模型临时更新次数,和前面的注释一样
loss = self.loss_func(self.forward(inputa, fast_weights, reuse=True), labela) # 计算内循环损失
grads = tf.gradients(loss, list(fast_weights.values()))
if FLAGS.stop_grad:
grads = [tf.stop_gradient(grad) for grad in grads]
gradients = dict(zip(fast_weights.keys(), grads))
fast_weights = dict(zip(fast_weights.keys(), [fast_weights[key] - self.update_lr*gradients[key] for key in fast_weights.keys()]))
output = self.forward(inputb, fast_weights, reuse=True)
task_outputbs.append(output)
task_lossesb.append(self.loss_func(output, labelb))
task_output = [task_outputa, task_outputbs, task_lossa, task_lossesb]
# meta 任务的输出数据
if self.classification: # 如果是分类任务
task_accuracya = tf.contrib.metrics.accuracy( tf.argmax(
tf.nn.softmax(task_outputa), 1), tf.argmax(labela, 1))
# 计算内循环训练数据准确率
for j in range(num_updates):
task_accuraciesb.append(tf.contrib.metrics.accuracy(tf.argmax(tf.nn.softmax(task_outputbs[j]), 1), tf.argmax(labelb, 1))) # 计算外循环验证数据的准确率
task_output.extend([task_accuracya, task_accuraciesb])
# 分类任务增加了训练和验证的准确率的输出
return task_output
if FLAGS.norm is not 'None':
# to initialize the batch norm vars, might want to combine this, and not run idx 0 twice.
unused = task_metalearn((self.inputa[0], self.inputb[0], self.labela[0], self.labelb[0]), False)
out_dtype = [tf.float32, [tf.float32]*num_updates, tf.float32, [tf.float32]*num_updates]
if self.classification:
out_dtype.extend([tf.float32, [tf.float32]*num_updates])
result = tf.map_fn(task_metalearn, elems=(self.inputa, self.inputb, self.labela, self.labelb), dtype=out_dtype, parallel_iterations=FLAGS.meta_batch_size) # 计算模型总输出
if self.classification:
outputas, outputbs, lossesa, lossesb, accuraciesa, accuraciesb = result
else:
outputas, outputbs, lossesa, lossesb = result
## Performance & Optimization
if 'train' in prefix: # 如果是训练阶段,需要对权值进行更新和优化目标函数
self.total_loss1 = total_loss1 = tf.reduce_sum(lossesa) / tf.to_float(FLAGS.meta_batch_size) # 内循环meta batch的总损失
self.total_losses2 = total_losses2 = [tf.reduce_sum(lossesb[j]) / tf.to_float(FLAGS.meta_batch_size) for j in range(num_updates)] # 外循环总损失
# after the map_fn
self.outputas, self.outputbs = outputas, outputbs
if self.classification: # 如果是分类任务
self.total_accuracy1 = total_accuracy1 = tf.reduce_sum(accuraciesa) / tf.to_float(FLAGS.meta_batch_size) # 内循环meta batch的准确率
self.total_accuracies2 = total_accuracies2 = [tf.reduce_sum(accuraciesb[j]) / tf.to_float(FLAGS.meta_batch_size) for j in range(num_updates)] # 外循环的准确率
self.pretrain_op = tf.train.AdamOptimizer(self.meta_lr).minimize(total_loss1)
# 最小化目标函数,即对内循环meta batch的总损失最小化优化
if FLAGS.metatrain_iterations > 0: # 训练迭代次数大于0
optimizer = tf.train.AdamOptimizer(self.meta_lr)
self.gvs = gvs = optimizer.compute_gradients( self.total_losses2[
FLAGS.num_updates-1]) # 外循环验证数据梯度计算
if FLAGS.datasource == 'miniimagenet':
# 如果是miniimagenet数据集,则需要对梯度进行区间(-10, 10)限制处理
gvs = [(tf.clip_by_value(grad, -10, 10), var) for grad, var in gvs]
self.metatrain_op = optimizer.apply_gradients(gvs)
# 外循环梯度反向传播更新模型权值
else: # 如果是测试阶段,不需要反向传播和优化目标函数,只需直接计算meta batch的内循环和外循环的准确度和损失
self.metaval_total_loss1 = total_loss1 = tf.reduce_sum(lossesa) / tf.to_float(FLAGS.meta_batch_size)
self.metaval_total_losses2 = total_losses2 = [tf.reduce_sum(lossesb[j]) / tf.to_float(FLAGS.meta_batch_size) for j in range(num_updates)]
if self.classification:
self.metaval_total_accuracy1 = total_accuracy1 = tf.reduce_sum(accuraciesa) / tf.to_float(FLAGS.meta_batch_size)
self.metaval_total_accuracies2 = total_accuracies2 =[tf.reduce_sum(accuraciesb[j]) / tf.to_float(FLAGS.meta_batch_size) for j in range(num_updates)]
- 运行代码进行实验
- 实验运行截图(本次实验主要是对分类任务的omniglot和miniimagenet数据集进行实验):
截图说明:本次实验结果的data_shape=(3,11),其中第一行数据是0~10次少量数据更新权值后计算测试集对应的准确率accuracy,第二行数据是0~10次少量数据更新权值后计算测试集对应的标准差,第三行数据0~10次少量数据更新权值后计算测试集对应的95%置信度。
图3 5-way, 1-shot omniglot测试结果截图
图4 5-way, 5-shot omniglot测试结果截图
图5 20-way, 1-shot omniglot测试结果截图
图6 20-way, 1-shot omniglot 运行截图(GPU显存不够,该实验无法完成)
图7 5-way, 1-shot mini imagenet测试结果截图
图8 5-way, 5-shot mini imagenet测试结果截图
- MAML实验结果整合(取上面11个结果对应的最好结果)
表1 本次报告MAML实验结果整合
| 数据集 |
5-way Accuracy |
20-way Accuracy |
||
| 1-shot |
5-shot |
1-shot |
5-shot |
|
| Omniglot |
98.77% |
98.81%+-0.2% |
90.03%+-0.5% |
- |
| MiniImagenet |
46.77%+-1.8% |
62.06%+-0.8% |
- |
- |
- 论文中的实验结果
图9 论文中的实验结果
- 结果分析与总结
通过分析Omniglot和MiniImagenet数据集中自己运行论文提供的代码得到的实验结果和论文中的结果对比,本次报告的实验结果基本接近论文的结果,说明了该论文提供的实验结果具有可信度和可重复性。通过阅读论文和理解论文的相应的代码,在论文的实验结果能够超前其前面论文的实验结果原因分析如下:(1)不同于前面的baseline的方法,改论文提出一个全新有效的方法,该方法是通过gradient by gradient去learning to learning,其核心方法是学会初始化模型的权值,而不是像之前fine tune那样随机初始化。该MAML训练好的模型,通过少量的数据集fine tune网络后能够快速使得模型达到不错的性能。(2)在图9中的最后两个结果中说明了,MAML方法性能提高是主要表现在一阶求导,而二阶求导对性能的提升起不到明显的作用,反而也会浪费了大量的二阶求导的时间。
引用:
- Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks[C]//Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017: 1126-1135.
- MAML github. https://github.com/cbfinn/maml Accessed Nov 10, 2019