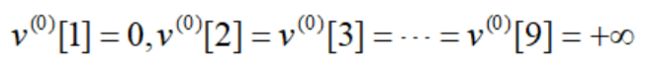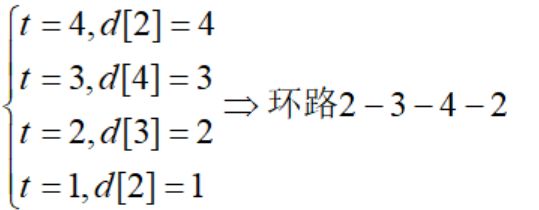最短路与动态规划(二)
1.一对多的无负权环路最短路问题可使用贝尔曼-福特算法求解
2.多对多的无负权环路最短路问题可使用弗洛伊德-瓦尔肖算法求解
3.迪杰斯特拉算法适用于一对多且路为非负的最短路问题
4.一对多的无环有向图也有最高效的算法
继上一篇最短路问题,我们介绍几种利用动态规划思想开发的算法。
传送门:最短路与动态规划(一)
1
一对多最短路算法
先介绍第一个无负权环路的最短路算法,由贝尔曼(R.E.Bellman)和福特(L.R.Ford)从函数方程启发而得的算法——贝尔曼-福特算法。为此,我们先引入记号:
我们先给出算法的详细流程:
我们以“双环”马戏团为案例,来感受一下该算法的全流程,起点为节点1,对于t=0,很显然有:
对于t=1,我们有:
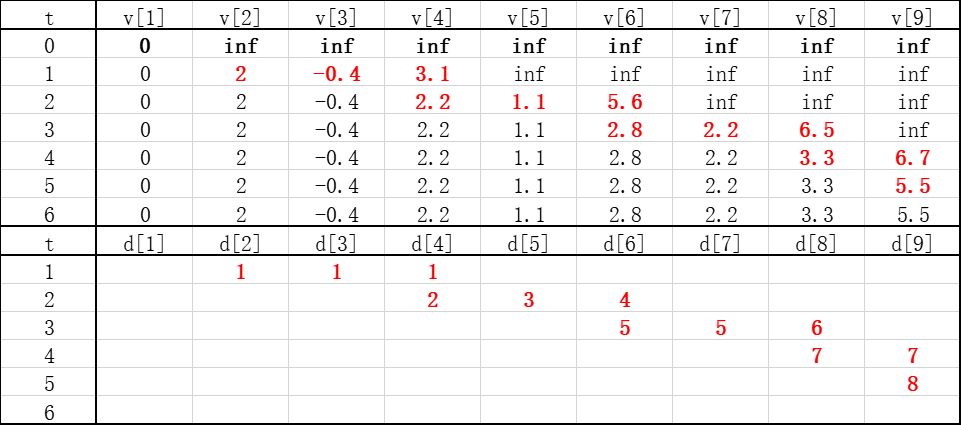
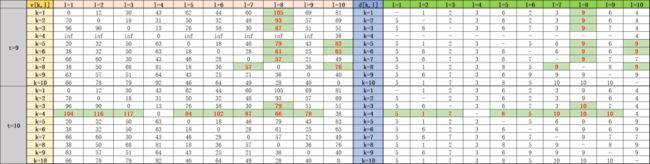
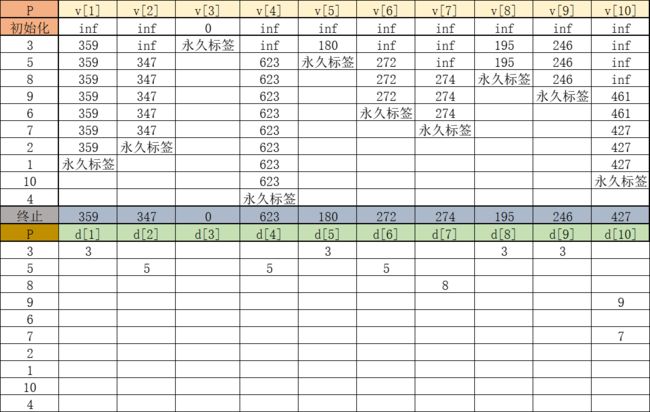
最终我们得到下面这张从t=0到6的表格,对应的d[k]进行更新:
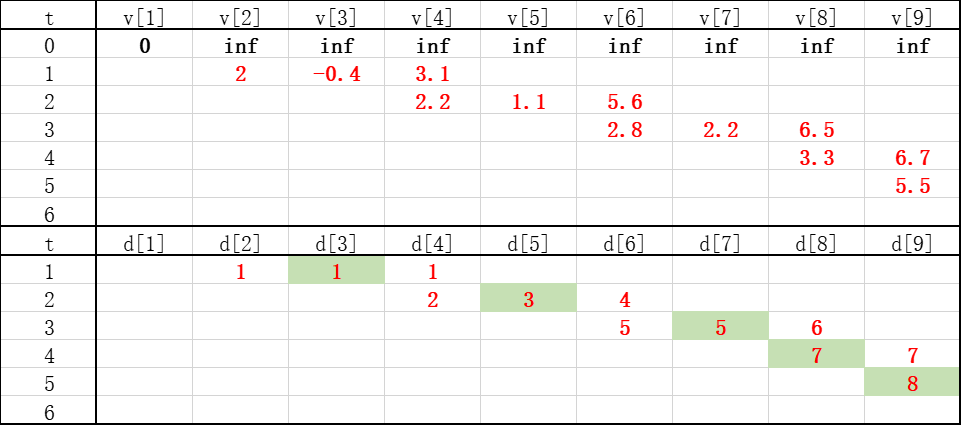
可以看到,从起点1到终点9的最短路长度是5.5(这里指成本),为了方面,我们做了简化,并且把最短路用绿色底色标注出来:
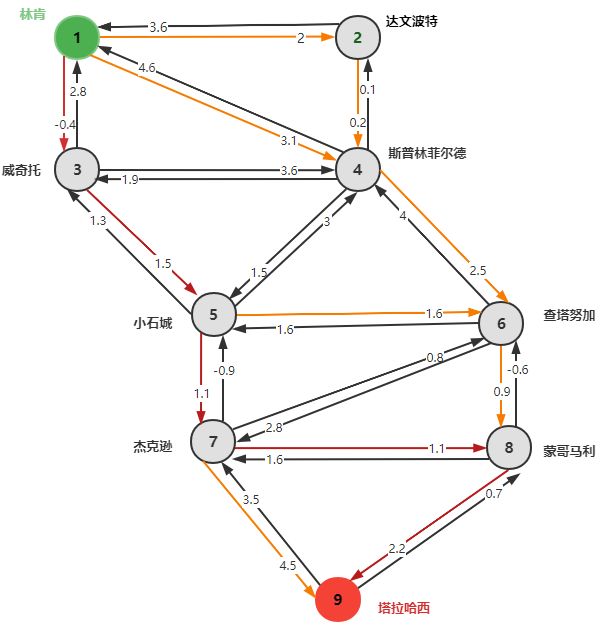
可以看到,从终点开始,t=5时刻的最短路上一个节点是8,t=4时节点8的上一个节点是7,以此类推,得到了最短路径:1-3-5-7-8-9,下图的红色路径就是最短路:
上面的算法能终止条件是图中不包含负权环路,如果遇到了负权环路,它就会不断变化,我们也可以用来判断一个图中是否包含负权环路。有原理:
如果贝尔曼-福特算法遇到了有负权环路的情况,那么当t=节点数后,v[k]仍有可能在不断变化,而仍在变化的节点处于那个负权环路之中
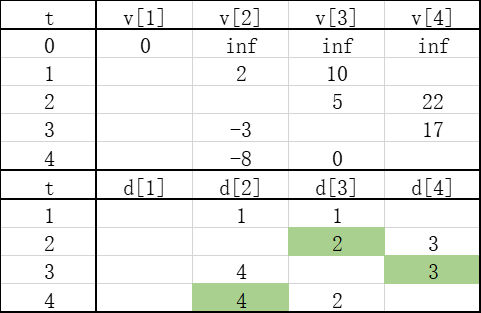
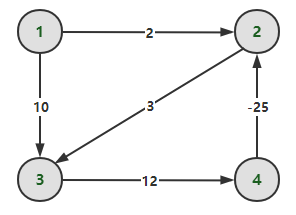
我们以上一篇的负权环路为例子,看看贝尔曼-福特算法的更新过程:
t=4时刻,达到了节点数,但v[k]没有停止变化,我们进行回溯有:
这就找到了负权环路。
2
多对多最短路算法
对贝尔曼-福特算法进行改进,就可以得到多对多的最短路算法,弗洛伊德-瓦尔肖算法——由弗洛伊德(R.W.Floyd)和瓦尔肖(S.Warshall)设计的算法。
这里唯一要注意的是,红色部分的t可能不是中介节点标号t,下面会举例加以说明。我们以利特尔维尔为例,展示弗洛伊德-瓦尔肖算法的全流程(代码附到最后)。
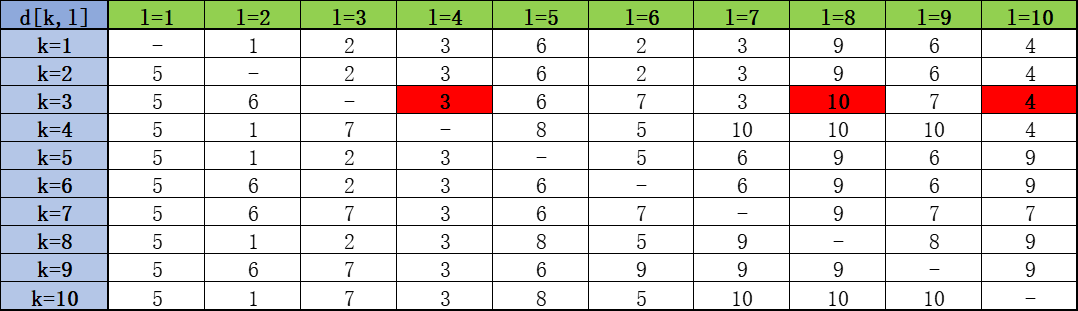
我们列出t=0到1和t=9到10的信息:
highlight的字体是相对上一次有变化的地方,更新原理按照算法的计算,这里要说明一下,对于t=10的v[4,1],我们计算得到:
但这里需要确定d[4,1],这里应该设为5而不是10.因为d[4,1]表示更新后的路的倒数第二个节点,应该从上一次循环中的d[10,1]中得到,即t=9时d[10,1]=5.
接下来的问题是,得到了最后的v和d,如何找到任意两个节点的最优路径,有原理:
求出节点k到节点l的最短路,可以通过从l出发,回溯其邻居节点d[k,l],以此类推直到到达起点k
比如要找到节点3到节点8的最短路,我们从v[3,8]=79知道最短路长度为79,其路径按照下面进行回溯(红色部分):d[3,8]=10,于是d[3,10]=4,进而d[3,4]=3,回到了起点3,因此路径为:3-4-10-8
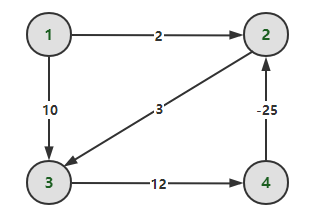
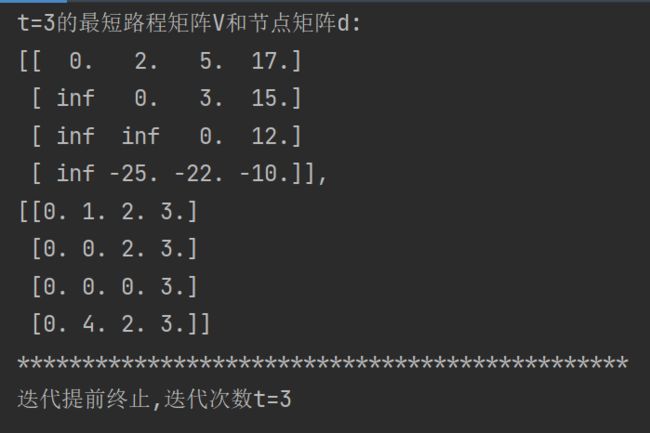
同样的,该算法也可以用于检验图中是否含有负权环路,仍以上一节负权环路的图为例子:
算法会在t=3停止迭代,其结果如下:
v[4,4]=-10,这告诉我们节点4在一个负权环路上,
我们进行回溯:d[4,4]=3,d[4,3]=2,d[4,2]=4,得到负权环路4-2-3-4
3
根据图特性定制高效算法
贝尔曼-福特算法和弗洛伊德-瓦尔肖算法可以解决没有负权环路的所有最短路问题。但当图满足更多条件的时候,这两个算法就不再是效率最高的算法了。对于一对多最短路问题,如果每条路的成本都是非负的,那么迪杰斯特拉算法(E.W.Dijkstra)具有更高的效率:
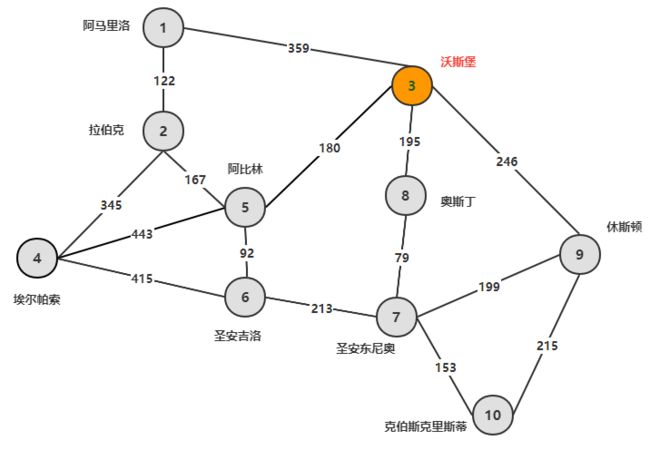
可以证明,迪杰斯特拉算法是计算一对多无负权的图最有效的方法。我们以德克萨斯运输公司为例,展现该算法的详细过程。
起点v[3]=0,因此p=3,步骤1更新过程为:
步骤3下一次p=5,再跳转回步骤1进行循环。
最后可以从表中直接得到从起点3到达其他节点的最短路长度。按照回溯方法可以得到最短路径,比如3到10,最短路径为3-8-7-10
迪杰斯特拉算法适用路是非负的一对多的最短路问题,包含有环路(注意,无负权环路不代表没有环路)的情况,如果图中的条件发生改变,对于一个无环图(必然仅含有弧,因为如果存在边,那么一条边的两个节点就可以构成一个有环子图),有更高效的的一对多无环有向图的最短路算法:
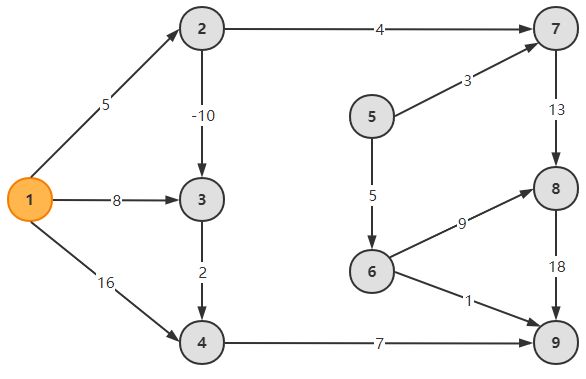
对于下图,起点是节点1,利用一对多无环有向图的最短路算法展示其全过程。
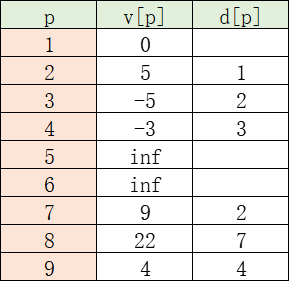
根据算法,起点s=0,然后p=2,值会被更新v[2]=0+5=5,d[2]=1.接下来节点p=3,v[3]=min{v[2]-10,v[1]+8}=-5,d[3]=2,以此类推,最后更新到节点9.最后利用回溯原理得到起点到任意节点的最短路径及长度。(该算法也开发了代码,已放在附录)
最后这里额外说明,对于最长路问题,只需要将这些算法的min替换为max,正无穷替换为负无穷即可。
附录:
#弗洛伊德瓦尔肖算法
import sys
import numpy as np
import pandas as pd
def Floyd_warshall(V):
'''
:param V: t=0时刻的v[k,l]矩阵,numpy格式
:return:
'''
t = 0
m,n = V.shape
try:
assert m == n
except AssertionError as e:
print('v[k,l]构成的原始矩阵不对, 请检查!')
sys.exit()
if not np.all(np.diagonal(V) == 0):
print('矩阵V对角元素不全为0,不符合图原则,请检查!')
sys.exit()
#更新d[k,l]矩阵,numpy格式
d = V.copy()
d[(d == 0) | (d == float('inf'))] = 0
for i in range(len(d)):
d[i, :][(d[i, :] != 0)] = i + 1
print('t=0的最短路程矩阵V和节点矩阵d:\n{},\n{}'.format(V,d))
print('***********************************************')
Ve,De = pd.DataFrame(),pd.DataFrame()
Ve = pd.concat([Ve, pd.DataFrame(V)], axis=0)
De = pd.concat([De, pd.DataFrame(d)], axis=0)
while t < n:
t += 1
for k in range(n):
for l in range(n):
if t-1 != l:
per_v = V[k,l]
V[k,l]=min(V[k,l],V[k,t-1]+V[t-1,l])
if V[k,l] < per_v:
d[k,l] = d[t-1,l]
print('t={}的最短路程矩阵V和节点矩阵d:\n{},\n{}'.format(t,V,d))
print('***********************************************')
Ve = pd.concat([Ve, pd.DataFrame(V)], axis=0)
De = pd.concat([De, pd.DataFrame(d)], axis=0)
if np.any(np.diagonal(V) < 0):
print('迭代提前终止,迭代次数t={}'.format(t))
break
return Ve,De
if __name__ == '__main__':
V = np.array(
[[0, 12, float('inf'),float('inf'),float('inf'),float('inf'),float('inf'),float('inf'),float('inf'),float('inf')],
[float('inf'), 0, 18, float('inf'),float('inf'),32, float('inf'),float('inf'),float('inf'),float('inf')],
[float('inf'),float('inf'),0, 13, float('inf'),float('inf'),30, float('inf'),float('inf'),float('inf')],
[float('inf'),float('inf'),float('inf'),0, float('inf'),float('inf'),float('inf'),float('inf'),float('inf'),38],
[20, float('inf'),float('inf'),float('inf'),0, 18, float('inf'),float('inf'),float('inf'),float('inf')],
[float('inf'),32, float('inf'),float('inf'),18, 0, 28, float('inf'),25, float('inf')],
[float('inf'),float('inf'),30, float('inf'),float('inf'),28, 0, float('inf'),21, 49 ],
[float('inf'),float('inf'),float('inf'),float('inf'),18, float('inf'),float('inf'),0, 36, float('inf')],
[float('inf'),float('inf'),float('inf'),float('inf'),float('inf'),25, 21, 36, 0, 40 ],
[float('inf'),float('inf'),float('inf'),float('inf'),float('inf'),float('inf'),49, 28, 40, 0]])
V,d = Floyd_warshall(V)
V.to_csv('V_matrix.csv',index=False)
d.to_csv('d_matrix.csv',index=False)import sys
import numpy as np
import pandas as pd
import networkx as nx
def Acyclic_Directed_Graph(df,s=1):
'''
一对多无环图最短路算法
:param df: 有向图dataframe,三列:source,target,weight
:param s: 一对多最短路算法的起点s,必须是节点中最小值,默认为1
:return:
'''
df['label'] = df['target'] - df['source']
df['label'] = df['label'].apply(lambda x:1 if x > 0 else 0)
a = list(set(df['target'])|set(df['source']))
v = dict.fromkeys(a,np.nan)
d = dict.fromkeys(a,'-')
if 0 in set(df['label']):
print('有向弧的节点命名不符合规则,source编码必须小于target,请检查')
sys.exit()
if s != min(a):
print('一对多算法的起点必须为所有节点最小值,请检查')
sys.exit()
v[s] = 0 #起点s最短路长度为0
deal_p = [s]
G = nx.from_pandas_edgelist(df,'source','target',edge_attr=["weight"],create_using=nx.DiGraph())
for p in sorted(v.keys()):
if p in deal_p:
continue
di = {i:v[i]+k['weight'] for (i,j,k) in G.in_edges(p,data=True)} #入弧
try:
i = min(di,key=di.get) #权重最小的入弧节点
v[p] = di[i]
d[p] = i
except ValueError as e:
v[p] = float('inf')
deal_p.append(p)
Re = pd.DataFrame([v.keys(),v.values(),d.values()]).T
Re = Re.rename(columns={0:'p',1:'v[p]',2:'d[p]'})
return Re