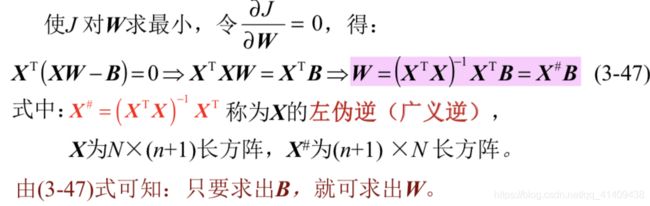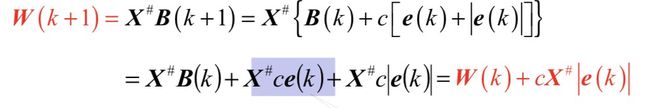模式识别—判别函数分类法（几何分类法）

统计模式识别之判别分析

统计模式识别:按任务类型划分

• 聚类分析(Clustering Analysis)——简称:聚类
  – 简单聚类方法:最大最小距离法
  – 层次聚类方法:分裂式、凝聚式
  – 动态聚类方法:C-均值，ISODATA
• 判别分析(Discriminatory Analysis)——简称:分类
  – 几何分类法(判别函数分类法):线性、分段线性、二次、支持向量机
  – 概率分类法(统计决策分类法):判别式 (Discriminative)、生成式 (Generative)
  – 近邻分类法(几何分类法和概率分类法的一种融合方法)
  所谓 几何分类法，是指在特征空间中，利用矢量空间的直观概念，使用
  代数方程方法，对模式进行分类。因此也被称为:代数界面方程法。
  所谓 概率分类法，是指把模式视为随机变量的抽样，利用统计决策理论 (贝叶斯决策理论)成熟的判决准则与方法，对模式样本进行分类。

判别函数

定义

判别函数是直接用来对模式进行分类的决策函数，也称判决函数或决策函数。

解释

若分属于ω₁，ω₂的两类模式在空间中的分布区域，可以 用一代数方程d(X) =0来划分，那么称d(X) 为判别函数， 或称决策函数。显然，这一方程表示的是n维空间的(n-1) 维超曲面(或超平面)

样例

示例:线性判别函数
d(X)=w₁x₁+w₂x₂+w₃
若d ( X ) > 0，则 X ∈ ω₁类;
若d ( X ) < 0，则 X ∈ω₂ 类;
若d(X)=0，则X ∈ω₁或X ∈ω₂ 或拒绝分类

维数N=3时:判别边界为一平面

维数N>3时:判别边界为一(N-1)维超平面 (记，直线为一维超平面;平面为二维超平面)

判断函数正负值的确定

判别界面的正负侧，是在训练判别函数的权值时人为确定的。 一般，令第1类样本的函数值大于零，第2类样本的函数值小于零

确定判别函数的两个因素

1. 判决函数d(X)的几何性质:它可以是线性的或非线性的函数，

2. 判决函数d(X)的系数:用所给的模式样本(可分)确定

线性判别函数

一般形式

将二维模式推广到n维，线性判别函数的一般形式为: d(X)=w₁x₁+w₂x₂+…+w_nx_n+w_n+1 =W₀^TX+w_n+1
式中: X = [x1 , x2 ,…, xn ]T
W =[w₁,w₂,…,w_n]T:权向量，即参数向量。
增广向量形式:
d(X)=w₁x₁+w₂x₂+…+w_nx_n+w_n+1 ⋅1
式中:
X =[x₁,x₂,…,x_n,1]^T 为增广模式向量
W = [w₁ , w₂ ,…, w_n , w_n+1 ]^T 为增广权向量

性质

两类情况

d(X)=W^TX
如果d(x)>0, 若X∈ω1 <0, 若X∈ω2
d(X) = 0:不可判别情况，可令 X ∈ ω₁或X ∈ ω₂或拒绝分类

多类情况

对M个线性可分模式类，ω₁， ω₂，… ω_M，有三种分类方式:

1. 多类情况1 是非两分法
   用线性判别函数将属于ωi类的模式与其余不属于ω_i类的模式分开。能用本方法分类的模式集称为 整体线性可分的
   
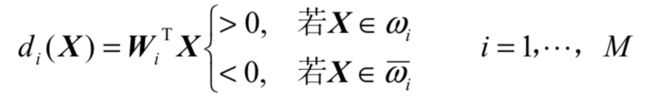
   识别出M类需要M个判别函数，有可能存在不确定区(indefinite region,IR)
2. 成对两分法
   一个判别界面只能分开两个类别，不需要把其余所有的类别都分开
   判决函数为: d_ij (X)=W_ig ^TX，这里d_ij = =d_ij
   判断函数性质：
   d_ij(X)>0, ∀j≠i;i,j=1,2,…,M, 若X∈ω_i
3. 成对两分法特例
   当ω_i /ω_j成对两分法中的判别函数dij(X)，如果可以分解为 d_ij (X) = d_i (X − d_j (X)

小结

(1)明确概念:线性可分。 一旦线性判别函数的系数W～k～被确定以后，这些函数就可以
作为模式分类器，对未知模式进行分类。
(2)ω_i / -ω_i与ω_i / ω_j
对于M类模式的分类， 两分法共需要M个判别函数，但成对两分法需要M(M-1)/2个。当时M>3时，后者需要更多的判别式(缺点)，但对模式集进行线性可分的可能性要更大一些(优点)
一种类别模式ω_i 的分布要比M-1类模式的分布更为聚集，因此 ω_i / ω_j两分法受到的限制比 ω_i / -ω_i 少，因此线性可分可能性大

广义线性判别函数

目的

通过某映射，把模式空间X变成X^*，以便让X空间中非线性可分的模式集，变成在X^*空间中线性可分的模式集

线性判别函数的几何性质

模式空间与超平面

概念

模式空间:以n维模式向量X的n个分量为坐标变量的欧氏空间
模式向量:点、有向线段
线性分类:用d(X)进行分类，相当于用超平面d(X)=0把模式空 间分成不同的决策区域

讨论

小结

1. 超平面 d(X) = 0 的法向量是权向量W₀
2. 超平面 d(X) = 0 的位置由 w_n+1 决定
3. 判别函数 d(X) 正比于点 X 到超平面的代数距离
4. 当 X 在超平面的正侧时 d(X) > 0，当 X 在超平面的 负侧时 d(X) < 0

权空间与权向量解

概念

权空间:以d(X)=w₁x₁+w₂x₂ +…+w_nx_n +w_n+1 的权系数为坐标变量的(n+1)维欧氏空间，X为已知。 增广权向量:W=(w₁,w₂, …,w_n,w_n+1)，点、有向线段

线性分类

判别函数形式已定，只需确定权向量
设增广样本向量:
ω₁ 类: X₁₁，X₁₂，…，X_1p
ω₂ 类: X₂₁，X₂₂，…，X_2q 使用d(X)将ω₁和 ω₂分开，需满足 d(X_1i)>0, i=1,2,…,p d(X_2i)<0, i=1,2,…,q

解空间

(p+q) 个训练模式将确定 (p+q) 个界面，每个界面 都把权空间分为两个半空间，(p+q) 个正的半子空间的 交空间是以权空间原点为顶点的凸多面锥

线性二分空间

线性判别函数的二分能力（Dichotomies）：是指线性函数对给 定的N个n维二类模式的全部可能的类别分布情况，能正确分类的情况数。线性判别函数的二分能力，称为线性二分能力

4个2维二类模式的类别分布总数为2⁴=16。用直线进行判别， 由图中可见，仅有2x7=14中情形可以判别。不可判别的两种 情形：(1) X₁和X₃为类1、X₂和X₄为类2；(2) 类别交换

Fisher线性判别

Fisher准则的基本原理：找到一个最合适的投影 轴，使两类样本在该轴上投影之间的距离尽可能 远，而每一类样本的投影尽可能紧凑，从而使分类效果为最佳

感知器算法

对线性判别函数，当模式维数已知时，判别函数的形式实 际上已经确定，如：三维时

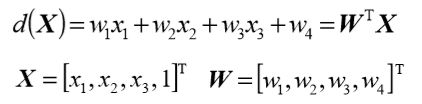
只要求出权向量，分类器的设计即告完成。本节开始介绍如何 通过各种算法，利用已知类别的模式样本训练权向量W

概念理解

1）训练与学习
训练：用已知类别的模式样本指导机器对分类规则进行反复修改，最终使分类结果与已知类别信息完全相同的过程。
学习：从分类器的角度讲
非监督学习
有监督学习<------>训练
2）确定性分类器
处理确定可分情况的分类器。通过几何方法将特征空间 分解为对应不同类的子空间，又称为几何分类器
3）感知器（Perceptron ）
一种早期神经网络分类学习模型，属于有关机器学习的仿生 学领域中的问题，由于无法实现非线性分类而下马（Minsky and Papert）。但“赏罚概念（reward-punishment ）”得到广泛应用

感知器算法

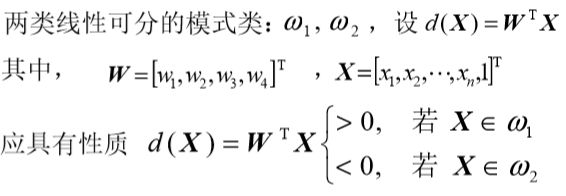
对样本进行规范化处理，即ω2类样本全部乘以(－1)，则有：
d(X = W^**T**X >0
感知器算法的基本思想：用训练模式验证当前权向量的合理性， 如果不合理，就根据误差进行反向纠正，直到全部训练样本都 被合理分类。本质上是梯度下降方法类

感知器算法的收敛性

收敛性：经过算法的有限次迭代运算后，求出了一个使所有样 本都能正确分类的W，则称算法是收敛的
可以证明：感知器算法是收敛的
收敛条件：模式类线性可分（即：存在一个权矢量与全部规 范化增广矢量的内积大于等于零）

梯度法

梯度概念

即：
梯度的方向是函数f(Y)在Y点增长最快的方向，
梯度的模是f(Y)在增长最快的方向上的增长率

梯度算法

思路

设两个线性可分的模式类ω₁和ω₂的样本共N个，ω₂类样本乘(-1)。将两类样本分开的判决函数d(X)应满足:
d(X_i)=W^TX_i >0 i=1,2,N——N个不等式

梯度算法的目的仍然是求一个满足上述条件的权向量，主导思想是将联立不等式求解W的问题，转换成求准则函数极小值的问题。

用负梯度向量的值对权向量W进行修正，实现使准则函数达 到极小值的目的。

实现方法

定义一个对错误分类敏感的准则函数J(W, X)，在J的梯度
方向上对权向量进行修改。一般关系表示成从W(k)导出W(k+1):

其中c是正的比例因子

固定增量法

定义

准则函数:J(W,X)=1/2(|W^TX| −W^TX)
该准则函数有唯一最小值“0”，且发生在W^TX > 0 的时候。 求W(k)的递推公式:

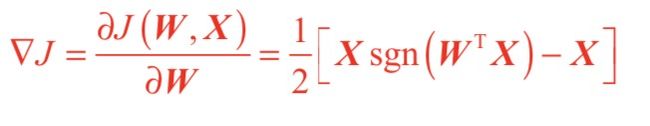
最小平方误差算法(LMS)

特点

• 对可分模式收敛。
• 对于类别不可分的情况也能指出来

原理

准则函数定义为：


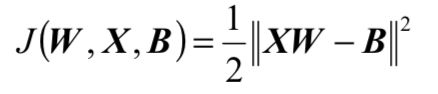
可以看出:
1 当函数J达到最小值，等式XW=B有最优解。即又将问
题转化为求准则函数极小值的问题。
2 因为J有两个变量W和B，有更多的自由度供选择求解，
故可望改善算法的收敛速率。

推导LMS算法递推公式

求W的递推公式

求B(k+1)的迭代式

求W(k+1)的迭代式

非线性判别函数