翻译:MICE 算法
原文:miceforest: Fast Imputation with Random Forests in Python
链式方程的多重插补(MICE,Multiple Imputation by Chained Equations)通过一系列迭代的预测模型来“填充”(插补)数据集中的缺失数据。在每次迭代中,将使用数据集中的其他变量来估算数据集中的每个指定的变量,这些迭代持续运行,直到满足收敛为止。
一,MICE的算法实现
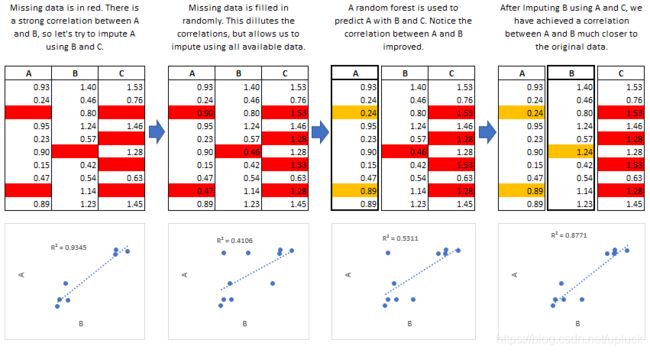
MICE的算法如下图所示,这个过程会持续执行,直到所有指定的变量都被插补为止。如果出现插补的均值没有收敛的情况,那么将会执行更多的迭代,尽管通常不需要超过5次迭代。
MICE适用的场景:
数据泄露(Data Leakage) :如果缺失值与目标变量直接相关联,从而导致泄漏,则MICE尤其有用。 例如,假设您要对客户保留率进行建模,在客户注册时或注册后1个月通过特定变量手机客户的登录信息,如果该变量的值缺失,这将导致数据泄漏,因为它告诉您“客户留存的时间没有超过1个月”。
Data Leakage定义:
存在和利用这种倒‘因’为‘果’的feature的现象,叫数据竞赛中的Data Leakage。 这里的Data Leakage 跟其他场合说的数据安全数据泄漏完全不一样。从字面上理解,我们说的Data Leakage不是数据泄漏,而是因果关系的纰漏,是由于数据准备过程中出现的失误,使模型沿着有纰漏的,甚至是颠倒的因果关系进行预测,但得到极好的预测结果。
举个例子,Chris老师在处理电信用户流失的时候,用原有的数据集轻轻松松就可以把AUC达到0.99以上。这让人非常警惕。于是Chris老师仔细查看了一下模型和数据,原来数据中有一个权重极高的feature是“3个月内的缴费纪录”。很多流失用户的账户内,这个feature的值是0。再进一步,他跟会计核实了一下,在会计记账中,这个feature 代表的是用户已经流失后的三个月的缴费纪录,那肯定就是0了。这是典型的因果关系颠倒。
漏斗分析(Funnel Analysis):信息通常是在“漏斗”的不同阶段收集的,MICE可用于对漏斗中不同阶段的实体特征进行有根据的猜测。
置信区间(Confidence Intervals):MICE可用于插补(估算)缺失值,但是请务必记住,这些估算值是一种预测,创建具有不同估算值的多个数据集可以执行两种类型的推断:
- 估算值分布:可以为每个估算值构建一个profile(画像,或特征),以获得该值可能的分布信息。
- 模型预测分布:使用多个数据集,您可以构建多个模型,并为每个样本创建预测的分布。那些具有估算值的样本,如果没有高置信度(插补值没有高置信区间),那么它们的预测值将具有较大的方差,很有可能具有很大的偏差。
二,预测均值匹配
miceforest可以利用称为预测均值匹配(predictive mean matching,PMM)的过程来选择要估算的值。 PMM包含从原始的、完整的数据中选择一个数据点,该数据点的预测值接近缺失样本的预测值。选择最接近的N个(mean_match_candidates参数)值作为候选值,从候选值中随机选择一个值,这个过程可以逐列指定。
MICE在实践中的工作原理如下图所示:

对于一个需要插补(估算)的变量,如果该变量具有以下任意特征,那么此方法非常有用:
- Multimodal(多模态)
- Integer(整数值)
- Skewed(偏斜)
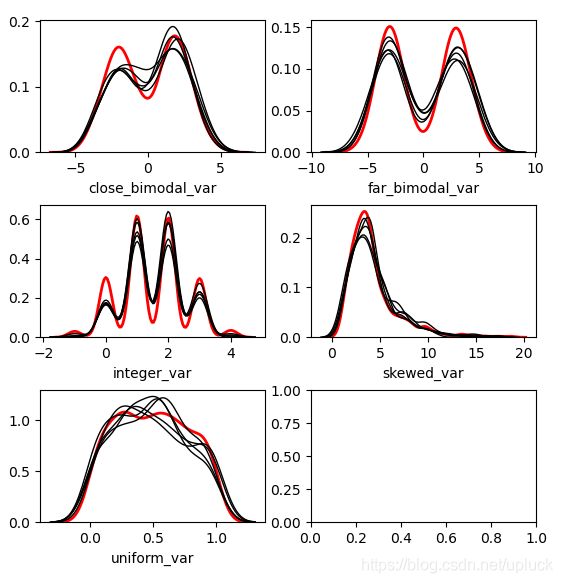
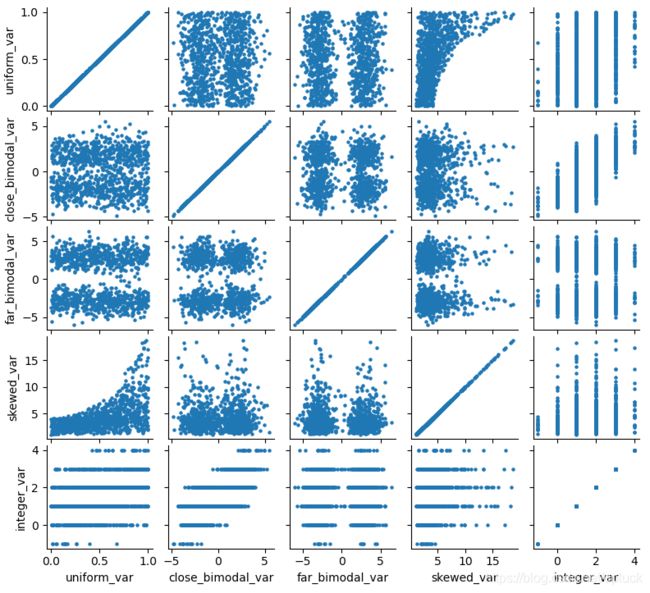
从下图中查看这三个特性的特点:
randst = np.random.RandomState(1991)
# random uniform variable
nrws = 1000
uniform_vec = randst.uniform(size=nrws)
def make_bimodal(mean1,mean2,size):
bimodal_1 = randst.normal(size=nrws, loc=mean1)
bimodal_2 = randst.normal(size=nrws, loc=mean2)
bimdvec = []
for i in range(size):
bimdvec.append(randst.choice([bimodal_1[i], bimodal_2[i]]))
return np.array(bimdvec)
# Make 2 Bimodal Variables
close_bimodal_vec = make_bimodal(2,-2,nrws)
far_bimodal_vec = make_bimodal(3,-3,nrws)
# Highly skewed variable correlated with Uniform_Variable
skewed_vec = np.exp(uniform_vec*randst.uniform(size=nrws)*3) + randst.uniform(size=nrws)*3
# Integer variable correlated with Close_Bimodal_Variable and Uniform_Variable
integer_vec = np.round(uniform_vec + close_bimodal_vec/3 + randst.uniform(size=nrws)*2)
# Make a DataFrame
dat = pd.DataFrame(
{
'uniform_var':uniform_vec,
'close_bimodal_var':close_bimodal_vec,
'far_bimodal_var':far_bimodal_vec,
'skewed_var':skewed_vec,
'integer_var':integer_vec
}
)
# Plot the original data
import seaborn as sns
import matplotlib.pyplot as plt
g = sns.PairGrid(dat)
g.map(plt.scatter,s=5)
二模态数据倾向于数据分为两个簇,偏斜分布说明数据的分布不是均匀的。
三,均值匹配的作用
上图中显示了变量的分布和相关性,让我们运行两次插补过程,一次使用均值匹配,一次使用模型预测,通过比较两次插补的结果来比较均值匹配的效果。
# Ampute the data.
ampdat = mf.ampute_data(dat,perc=0.25,random_state=randst)
# Create kernel
kernelmeanmatch <- mf.MultipleImputedKernel(ampdat,mean_match_candidates=5)
kernelmodeloutput <- mf.MultipleImputedKernel(ampdat,mean_match_candidates=0)
kernelmeanmatch.mice(5)
kernelmodeloutput.mice(5)
案例1,使用均值匹配
kernelmeanmatch.plot_imputed_distributions(wspace=0.2,hspace=0.4)
kernelmodeloutput.plot_imputed_distributions(wspace=0.2,hspace=0.4)
注:红线是原始数据,黑线是每个数据集的插补(估算)值。
从案例1和2中,可以看到均值匹配的效果更好,具体情况取决于数据的分布。从直观上来看,简单地从模型预测中返回值,虽然可能会提供更好的“拟合”,但是并不能为插补值提供跟原始值相似的分布。这可能是有益的,具体取决于您的目标。