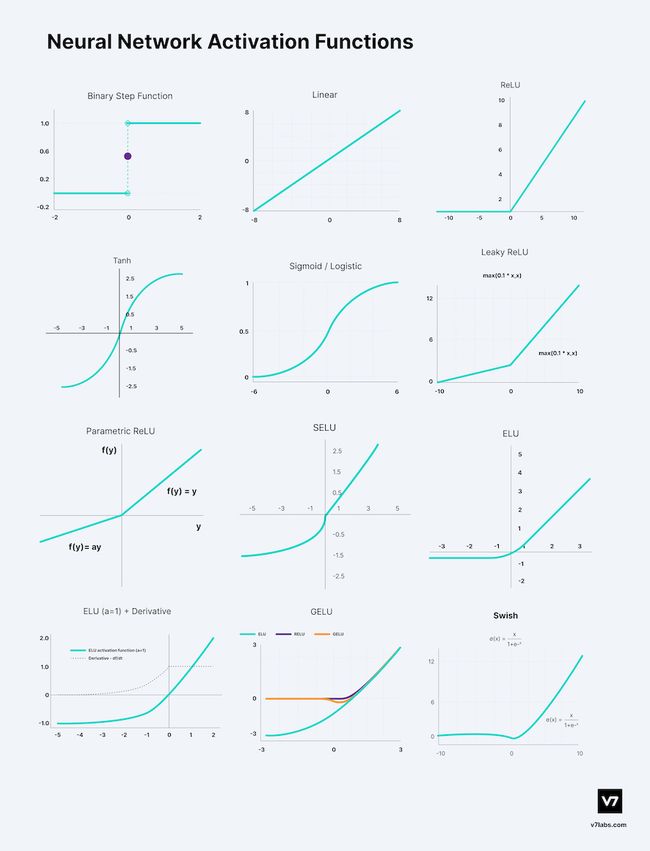
【Pytorch基础教程35】引入非线性的激活函数

一、从最简单的logistic回归说起

线性分类模型一般是一个广义线性函数，即一个或多个【线性判别函数】加上一个【非线性激活函数】，所谓“线性”是指决策边界由一个多个超平面组成。通过引入S型的对数几率函数$$y=\frac{1}{1+e^{-z}}$$该激活函数作用是因此引入非线性：

逻辑回归即线性回归+sigmoid函数，是最基础也是最重要的模型：

通过逻辑回归能演化出很多模型：

• 逻辑回归=线性回归+sigmoid激活函数，从而将回归问题转换为分类问题
• 逻辑回归+矩阵分解，构成了推荐算法中常用的FM模型
• 逻辑回归+softmax，从而将二分类问题转化为多分类问题
• 逻辑回归还可以看做单层神经网络，相当于最简单的深度学习模型

二、为什么需要激活功能

• 使用非线性激活函数的原因是线性模型的表达能力不够，通过对输出结果应用激活函数而引入非线性变换。
  • 什么是非线性？从模型举例，如GBDT+LR（通过GBDT构建非线性特征，即，然后送入LR进行做CTR）。
  • 比如说，有一天你发现“ID 为 233 的用户喜欢买各种钢笔”这个事实，它可以有两个特征组合出来，一个是“ID 为 233”，是一个布尔特征，另一个是“物品为钢笔”，也是一个布尔特征，显然构造一个新特征，叫做“ID 为 233 且物品为钢笔”，即非线性特征。
• 如果不用激活函数，每一层输出都是上一层输入的线性函数，那么每一层的输出都是输入的线性组合，与只有一个隐藏层的效果是一样的。引入非线性函数后才使得深层神经网络有意义（可以逼近任意函数）。

三、常见激活函数特点：

（1）非线性
（2）可微性：因为在反向传播更新梯度时，需要计算损失函数对权重的偏导数，传统的激活函数sigmoid满足出处可微，而ReLU函数仅在有限个点处不可微。对于随机梯度下降（Stochastic Gradient Descent，SGD）算法，几乎不可能收敛到梯度接近0的位置，所以优先的不可微点对于优化结果影响不大。
（3）单调性：保证单层网络为凸函数；单调性说明其导数符号不变，使得梯度方向不会经常改变（从而让训练更容易收敛）
（4）f(x)≈x
（5）输出值范围：

• 对激活函数的输出结果进行范围限定（有助于梯度平稳下降，如Sigmoid、tanh），
• 但对输出值范围限定会导致梯度消失问题；强行让每一层的输出结果控制在固定范围会限制神经网络的表达能力，而输出值范围为无限的激活函数（如ReLU函数），对应模型的训练过程更加高效，此时一般需要使用更小的学习率。

（6）计算简单、归一化

3.1 ReLU激活函数

relu是针对sigmoid和tanh饱和区间的问题而提出的激活函数，其函数形式和求导结果都很简单：
$$\begin{array}{c}\delta (x)=\max (0,x)\\ {\delta }^{\prime }(x)=\{\begin{array}{ll}0& \mathrm{x}<=0\\ 1& \mathrm{x}>0\end{array}\end{array}$$

优点：
（1）ReLU函数的线性特点使得其收敛速度比Sigmoid、tanh更快，而且没有梯度饱和、梯度消失的情况出现。
（2）计算更加高效，相比于sigmoid、tanh函数，ReLU只需要一个阈值就可以得到激活值（不需要指数运算），不需要对输入归一化来防止达到饱和。

缺点：
（1）ReLU的输出不是0均值
（2）Dead ReLU Problem(神经元坏死现象)：ReLU在负数区域被kill的现象叫做dead relu。ReLU在训练的时很“脆弱”。在x<0时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新

3.2 sigmoid激活函数

取值范围为(0, 1)，可用来做二分类任务。$$S(x)=\frac{1}{1+e^{-z}}=\frac{e^x}{e^x+1}$$
Sigmoid优点：输出范围有限，所以数据在传递过程中不易发散；还有容易求导。
Sigmoid缺点：梯度下降非常明显，且两头过于平坦，容易在反向传播时，出现梯度消失的情况，输出的至于不对称（并非像tanh函数那样是-1~1）

对sigmoid函数进行求导：$$\begin{array}{rl}{\sigma }^{\prime }(x)& \\ & ={\left(\frac{1}{1+e^{-x}}\right)}^{\prime }\\ & =\frac{e^{-x}}{{\left(1+e^{-x}\right)}^2}\\ & =\frac{e^{-x}+1-1}{{\left(1+e^{-x}\right)}^2}\\ & =\frac{1}{1+e^{-x}}-\frac{1}{{\left(1+e^{-x}\right)}^2}\\ & =\frac{1}{1+e^{-x}}\left(1-\frac{1}{1+e^{-x}}\right)\\ & =\sigma (x)\left(1-{\sigma }^{\prime }(x)\right)\end{array}$$

3.3 tanh激活函数

双曲正切函数，取值范围为[-1, 1] $$\mathrm{Tanh}(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
优点：相对于sigmoid，tanh是0均值的
缺点：仍存在梯度饱和，和由于是指数形式，计算复杂度高的问题

对tanh函数进行求导：
$$\begin{array}{rl}{\tanh }^{\prime }(x)& \\ & ={\left(\frac{e^x-e^{-x}}{e^x+e^{-x}}\right)}^{\prime }\\ & =\frac{{\left(e^x-e^{-x}\right)}^{\prime }\left(e^x+e^{-x}\right)-\left(e^x-e^{-x}\right){\left(e^x+e^{-x}\right)}^{\prime }}{{\left(e^x+e^{-x}\right)}^2}\\ & =\frac{{\left(e^x+e^{-x}\right)}^2-{\left(e^x-e^{-x}\right)}^2}{{\left(e^x+e^{-x}\right)}^2}\\ & =1-{\left(\frac{e^x-e^{-x}}{e^x+e^{-x}}\right)}^2\\ & =1-{\tanh }^2(x)\end{array}$$

3.4 softmax激活函数

softmax通常来讲是激活函数，但是softmax函数要与交叉熵损失函数一起使用来避免数值溢出的问题。所以，在常见的深度学习框架中（比如torch和paddle中），在网络构造中通常是看不见softmax函数的，而在我们调用交叉熵损失函数时(entropy)，框架会在entropy之前自动为我们添加softmax函数。

• torch中使用nn.CrossEntropyLoss时，网络最后不需要进行softmax，该函数会进行log_softmax的操作：
  • pred的类型需要时浮点型，而target的类型需要时long类型torch.LongTensor()，不然会报错
  • target不需要转化成one-hot形式，只需要[0,1,2,3,4,…]即可，CrossEntropy中自动进行转化为one-hot格式。注意下图右侧是由类别1生成独热编码向量。

（1）交叉熵手写版本

import numpy as np
y = np.array([1, 0, 0])
z = np.array([0.2, 0.1, -0.1])
y_predict = np.exp(z) / np.exp(z).sum()
loss = (- y * np.log(y_predict)).sum()
print(loss)
# 0.9729189131256584

（2）交叉熵pytorch栗子

交叉熵损失和NLL损失的区别（读文档）：

• https://pytorch.org/doc s/stable/nn.html#crossentropyloss
• https://pytorch.org/docs/stable/nn.html#nllloss
• 搞懂为啥：CrossEntropyLoss <==> LogSoftmax + NLLLoss

3.5 其他激活函数

四、常见问题

4.1 RNN能否使用ReLU作为激活函数

可以。当采用ReLU作为RNN中隐藏层的激活函数时，只有当W的取值在单位矩阵附近时才能取到较好的效果（因此要将W初始化为单位矩阵），实验证明这样做后能在一些应用与LSTM取得相似的结果，且学习速度更快。

Reference

[1] Activation Functions in Neural Networks
[2] 夯实基础知识——常见激活函数总结