第三章 灰度变换与空间滤波
文章目录
-
- 数字图像处理 第三章灰度变换与空间滤波
- 引言
- 3.1背景知识
- 3.2灰度变换
-
- 3.2.1灰度变换函数
-
- 图像翻转
- 对数变换
- 伽马变换
- 分段变换函数
- 3.2.2直方图处理
-
- 直方图均衡
- 直方图匹配
- 局部直方图处理
- 3.3空间滤波
-
- 3.3.1平滑滤波器
- 3.3.2锐化滤波器
数字图像处理 第三章灰度变换与空间滤波
引言
空间域指图像平面本身,这类图像处理方法直接以图像中的像素操作为基础,这正是相对于下一章变换域而言的。空间域处理主要有灰度变换和空间滤波。灰度变化在单个像素上进行,主要以对比度和阈值处理为目的;空间滤波则涉及改善性能的操作。
3.1背景知识
在本次所讨论的理论以及实验都是在空间域上进行的,空间域技术直接在像素上进行操作。通常来说,空间域技术在计算上会更加有效,并且在执行上需要较少的处理资源。
在这一章中,我们主要使用灰度变换函数来进行图像增强。图像增强是指对图像的某些特征如边缘、轮廓、对比度等来进行加强。今天所学的灰度变换和空间滤波正是图像增强的两种方法。
3.2灰度变换
灰度变换是所有图像处理最简单的技术。通过灰度变换来进行对比度处理和阈值处理。
3.2.1灰度变换函数
r和s分别代表处理前后的像素值。s=T(r),通过关系式T,将像素值r映射到像素值s的一种变换。
图像翻转
通过翻转公式
s=L-1-r
使用这种方式翻转一幅图像的灰度级可以得到等效的照片底片。这种处理特别适合增强图像的暗区域的白色或者是灰色细节,尤其是当黑色面积占据主体地位时候。
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('E:\\picture\\tupian.png')
gray_image = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
height = gray_image.shape[0]
width = gray_image.shape[1]
result = np.zeros((height, width), np.uint8)
for i in range(height):
for j in range(width):
gray = 255 - int(gray_image[i, j])
result[i, j] = np.uint8(gray)
cv2.imshow("gray image", gray_image)
cv2.imshow("result", result)
cv2.waitKey(0)
cv2.DestoryAllWindows()
对数变换
对数变换的通用形式为
s=clog(1+r)
其中c是一个常数,对数曲线的形状表明,该变换将输入中范围较窄的低灰度值映射为输出中较宽范围的灰度值,相反对高的输入灰度值也是如此。通过这种变换来扩展图像中的暗像素的值,同时来压缩更高灰度级的值。
import cv2
import numpy as np
from matplotlib import pyplot as plt
def log_plot(c):
x = np.arange(0, 256, 0.01)
y = c * np.log(1 + x)
plt.plot(x, y, 'r', linewidth=1)
plt.rcParams['font.sans-serif'] = ['simHei']
plt.title(u'对数变换函数')
plt.xlim(0, 255), plt.ylim(0, 255)
plt.show()
def log(c, img):
output = c *np.log(1.0 + img)
output = np.uint8(output + 0.5)
return output
img = cv2.imread('E:\\picture\\tupian.png')
log_plot(42)
result = log(42,img)
cv2.imshow("image", img)
cv2.imshow("result", result)
cv2.waitKey(0)
cv2.DestoryAllWindows()
伽马变换
伽马变化公式,s=crγ,其中c和γ为正常数。我们可以知道,γ>1的值与γ<1的值所生成的曲线的效果是完全相反的。当γ=1时,进行的是恒等变换。
当然还有一些用来矫正幂律响应现象的处理称之为γ校正。其实就是在将图像输入到监视器的时候进行预处理,即对幂次方去倒数变换。
下面进行伽马值不同的两个实验。
分段变换函数
(1)对比度拉伸
图像对比度指的是一幅图像中明暗区域最亮的白和最暗的黑之间不同亮度层级的测量,或者说是一幅图像灰度反差的大小。对比度越大,图像越清晰醒目,色彩也越鲜明艳丽;而对比度小,则会让整个画面呈现灰色的。
Imax = np.max(farina)
Imin = np.min(farina)
MAX = 255
MIN = 0
farina_cs = (farina - Imin) / (Imax - Imin) * (MAX - MIN) + MIN
cv2.imshow("farina_cs", farina_cs.astype("uint8"))
cv2.waitKey()
通过以上代码把图像拉伸到灰度空间的最大值以及最小值,来进行对比度拉伸,再看直方图就可以看见充满整个直方图。
(2)灰度级分层
是突出图像中特定灰度范围的亮度,一种方法是将感兴趣范围内的所有灰度值显示为一个值,而将其他灰度值显示为另外一个值;第二种方法是保持图像中其他灰度级不变,将自己感兴趣的范围的灰度变亮或者是变暗。
(3)比特平面分层
像素是比特组成的数字。我们一般用8比特来表示一个像素,所以我们就可以提取出不同的比特平面的灰度图。比特平面分层可以压缩图像,但是经过试验,用四个高阶比特平面来恢复图像较好,所以就可以用四个高阶比特平面来压缩保存图像较好。
3.2.2直方图处理
直方图是多种空间域处理技术的基础。图像直方图反映了图像像素分布的统计特性,是图像处理中简单有效的工具。我们可以知道在暗图像中,直方图的分量集中在灰度级的低端,亮图像则集中在直方图的高端。
直方图均衡
直方图均衡是一种增强图像的方法,其主要思想是将一副图像的直方图分布通过累积分布函数变成近似均匀分布,从而增强图像的对比度。
将之前以上的原图的灰度直方图与均衡过的直方图放在一起。
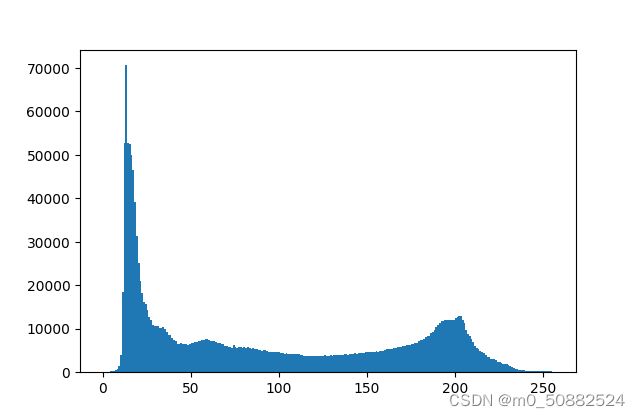
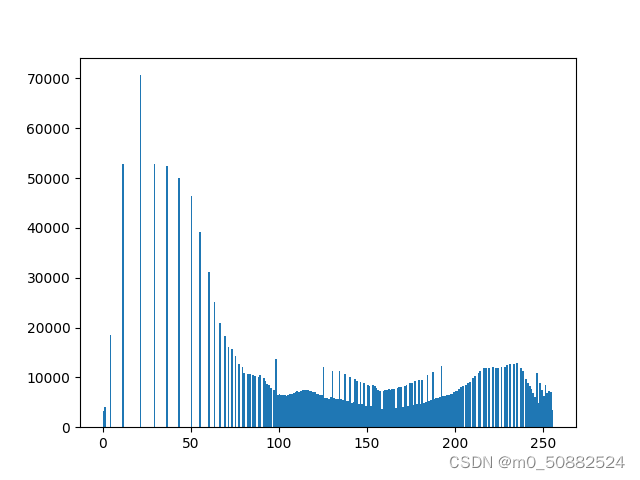
由图可以看出明显有所变好。
直方图匹配
直方图均衡能够自动 的确定变换函数,该函数寻求产生有均匀直方图的输出图像,当需要自动增强时,均衡化很有用,因为它的结果可通过计算得知,且容易实现。但对于图片处理后出现特殊情况的时候,就要使用另一种方法了,这种方法我们称为直方图匹配或规定化。
局部直方图处理
前面讨论的直方图处理都是全局性的,但是也存在这样的情况,需要增强图像中的小区域的细节,这样就需要局部增强。
3.3空间滤波
空间滤波是图像处理广泛运用的主要工具之一。滤波一词借用于频域处理。滤波就是接受或者拒绝一定的频率量。如通多低频的就叫做低频滤波器。
即将一个小矩阵扣在图像上,通过对应算子进行数学操作,然后将新的数值赋予模板中心,然后延续下去。
3.3.1平滑滤波器
平滑空间滤波器用于模糊处理和降低噪声。模糊处理经常用于预处理当中。如在目标提取之前先取出图像中的一些琐碎细节。可以通过线性滤波或者是非线性滤波来降低噪声。
均值滤波器是简单的平滑滤波器。它使用滤波器模板确定的邻域内像素的平均值来代替图像中每个像素的值。
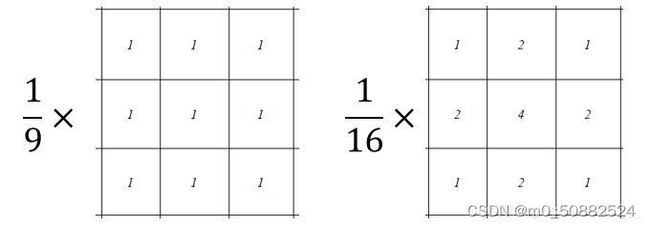
这种3x3`滤波器,我们可以有式子看出他的作用,模糊处理,降低噪声。
3.3.2锐化滤波器
前面所介绍的平滑滤波器是用于模糊处理和降低噪声,然后锐化滤波器恰恰相反是为了突出图像的突变信息,图像的细节和边缘。上一节介绍到图像模糊可以在空间域使用像素领域平均法来实现。且因为均值处理与积分相似,所以我们就会想到与积分相反的微分来进行锐化处理。锐化滤波器则使用邻域的微分作为算子,增大邻域间像素的差值,使图像的突变部分变的更加明显。
图像处理中一阶微分是用梯度幅值在实现的,用sobel算子处理一阶微分。
对于函数f(x,y),f在坐标(x,y)处的梯度定义为二维列向量

后面其幅度值也可以近似用平方和开根号以及绝对值来表示。
M(x,y)=|gx|+|gy| 亦或者是对gx的平方与gy的平方和开根号。
用程序实现如下。
img = cv2.imread('E:\\picture\\te.png')
x = cv2.Sobel(img[:, :, 0],cv2.CV_16S, 1, 0)
y = cv2.Sobel(img[:, :, 0],cv2.CV_16S, 0, 1)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
res = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
cv2.imshow("result",res)
cv2.imshow("origin",img)
cv2.waitKey(0)