DIP笔记3——灰度变换与空间滤波
1 基础
空间域：图像本身，也就是包含图像像素的平面（因为有频率域，所以起了个怪名字）
涉及空间域的操作主要就是处理像素（反之，频率域不处理图像本身像素），而空间域处理方法主要有两种，叫做：
1.灰度变换 和 2.空间滤波
灰度变换：对图像的单个像素进行操作，主要目的是 对比度和阈值处理
对比度是指投影图像最亮和最暗区域之间的比率，比值越大，从黑到白的渐变层次就越多，从而色彩表现越丰富。
空间滤波：对图像的单个像素的邻域处理，主要目的：改善性能（如锐化）
二者都会遍历所有像素点，区别是：灰度变换只关注当前像素点（那一个小格子），空间滤波会关注当前像素和周围的邻域（特殊情况：邻域大小可以是1*1，此时就是灰度变换。一般是9宫格，3*3邻域）
空间滤波器：（别名：空间掩模、核、模板、窗口）介绍
邻域与预定义操作一起被称为空间滤波器（冈萨雷斯）
邻域就是像素周围的小矩阵1x1,3x3...；预定义操作指的是 对邻域像素 的线性操作（累乘求和）或非线性操作（比大小，用中值等等）
总结：空间滤波器 = 邻域 + 对邻域的操作
灰度变换——对比度拉伸 、阈值处理
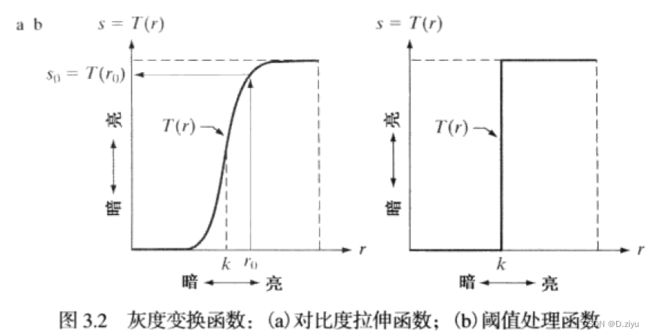
联系：二者都是让 低于k 的灰度变暗，高于k的灰度变亮
区别：阈值处理一棒子打死，是二值化，不是暗就是亮；对比度拉伸，变换更平缓，灰度级更多
2 一些灰度变换函数
- 线性函数
- 对数函数
- 幂函数
- 分段线性变换函数
各种函数变化曲线：
2.1 线性变换——图像反转
适用于：增强暗区域上的白色灰色细节
作用举例：
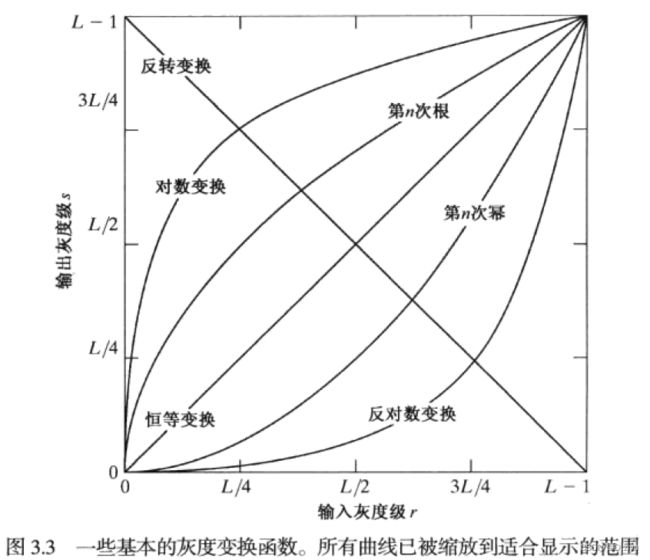
2.2 对数变换
整体灰度值变大，图像整体变亮。
将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度值
如上图3.3中，[0, L/4] 的灰度区域变为 [0, 3L/4]
反之亦然
应用1：处理普通图像，但被伽马变换取代
应用2：频谱图，涉及4频率域。
作用，与频率域有关的不懂！
2.3 幂（伽马）变换
公式： s = c r γ s = cr^\gamma s=crγ
γ \gamma γ < 1时，将较窄范围的输入灰度------->较宽范围的输出灰度(相似 对数变换 )
γ \gamma γ > 1，(相似于 反对数变换)
区别：此处的 γ \gamma γ 改变，能得到一系列函数，对数变换不行
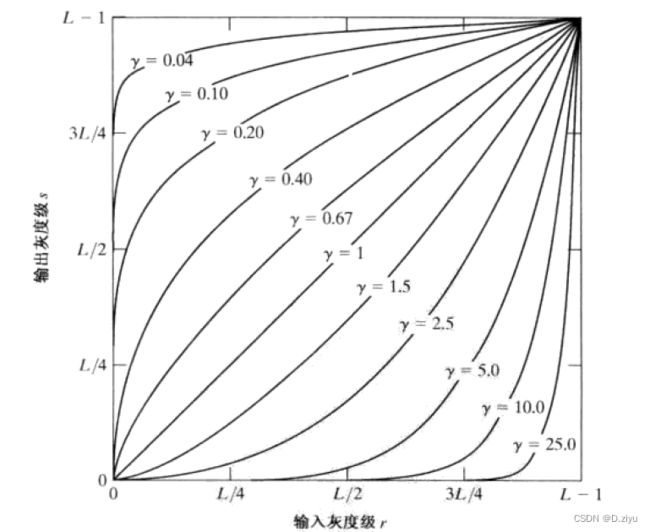
作用：1.伽马校正 2.对比度增强
用于图像获取、打印和显示的各种设备根据幂律来产生响应。
用于校正这些幂律响应现象的处理称为伽马校正（冈萨雷斯）
以前CRT显示器，输出亮度比输入的低，是幂次关系，所以用伽马校正处理。后来这些设备淘汰了，而伽马变换就更多作用于图像的对比度增强上；人眼恰好对较暗值比较敏感，对较亮值不太敏感，而伽马变换保留暗部细节，改善图像质量
参考
2.4 分段线性函数
是前三种的补充，优点：形式可以任意复杂；缺点：要求用户输入很多参数
说明：相对于前面普通线性曲线，变复杂了；输入很多参数，如下图中的（r1,s1）,(r2, s2)，每张图片的这几个参数都要自己输入，很麻烦！
2.4.1 对比度拉伸变换
最简单的分段线性函数之一。
作用：扩展图像灰度级范围
对比度拉伸
对比度增强，易混淆
以下为对比度拉伸变换经典案例：
·
当时怎么都看不懂这句话，以为(r1,s1) = (0,0),（r2,s2）=（L-1,L-1），那不就是原图像了吗？怎么就拉伸到[0，L-1]了？
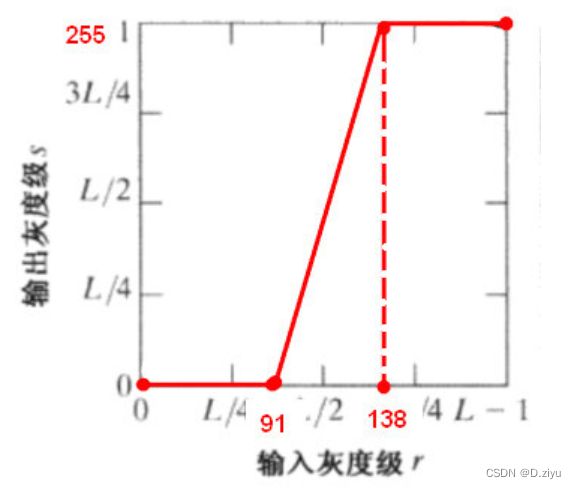
原来，图3.10.a只是形式，并不代表此处函数图真的是这个。(b)中，最低灰度级为91，最高灰度级为138，并且要将灰度值拉伸至[0, 255]。故实际图如下：
这样就完成了[91,138] 到 [0,255] 的拉伸 参考
2.4.2 灰度级分层
作用：突出图像中特定灰度范围的亮度
1 突出[A,B]范围灰度，其它范围反方向变化
2 只变感兴趣范围[A,B]（可暗可亮）,其它不变
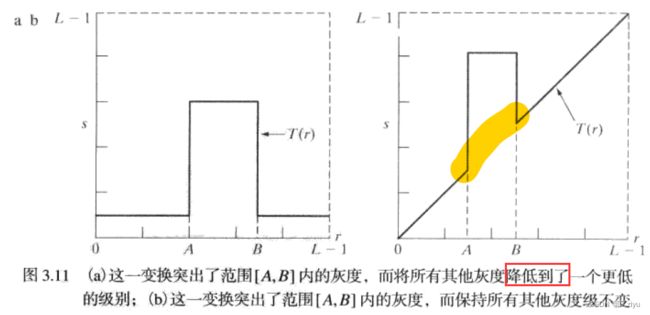
图a为原图；b将高灰度的血管部分加亮，其余变暗；c将感兴趣区域（灰雾状）变暗，其余不变
2.4.3 比特平面分层
问：为什么他是分段线性函数里的？？？
与突出灰度级范围不同的是，可以突出特定比特整个图像外观作出贡献
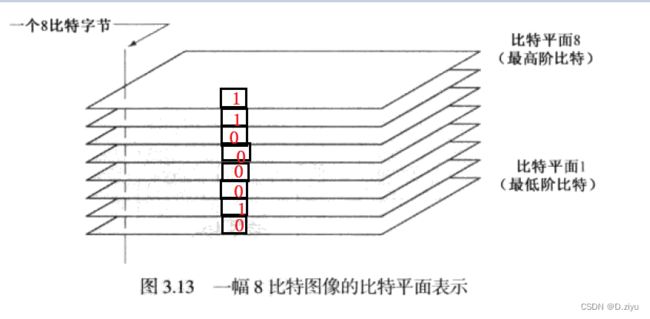
以256灰度级为例， 2 8 = 256 2^8 = 256 28=256 , 故一个像素的灰度由8位组成
解释图：
所有像素的最低位组成 比特平面1，以此类推…
下面是经典案例：
最低边界中间点像素灰度值为194（那个红点），二进制 1 1 0 0 0 0 1 0
观察可得，高阶比特平面包含了大多比特数据，低阶比特平面有更多灰度细节
只是看出来的吗？有原因吗？？？
获取每个比特平面的方法 参考
答：将像素灰度值 和 2^(n-1)按位与运算
作用1：突出特定比特层(灰度级范围)来突出整个图像的外观
比如，将最高比特层全部置1，代表所有像素都在127~255间，让图像变亮
作用2：图像压缩：如将图像中5、6、7、8阶比特平面的信息保留后，将图像重建，可通过50%的储存量体现图像绝大部分的外观信息。
图像重建的过程是将第n个比特平面的像素值乘以2的n-1次幂后叠加。
3 直方图
3.1 直方图均衡
Q1. 什么情况使用直方图均衡
答：lena找我给她照相，我拍照技术很烂，照了好多图片，都不能看（如下），现在需要将对比度增强，用什么方法呢，2.4.1 学的分段线性变换吗？NO，几百张图，每张输入的两个点参数还不一样。所以要一种省时省力，无需调参的自动对比度增强技术。这类技术中最基本的一种就是：直方图均衡化
顾名思义，让输出图像的灰度直方图变均匀
基本思想：把原始图像的灰度直方图从比较集中的某个灰度区间变成全部灰度范围内的均匀分布
具体的做法：通过对图像进行非线性拉伸，重新分配图像的像素值，使一定灰度范围内的像素数量大致相同。
Q. 什么是归一化？为什么要做归一化？
答：归一化就是让该灰度级像素个数/总像素个数,即 n k / M N n_k / MN nk/MN ，纵坐标用概率P表示；归一化的好处：
- 使函数值正则化到[0,1]区间; (不懂)
- 成为实数函数函数值的范围与象素的总数无关
- 给出灰度级r在图像中出现的概率密度统计（不懂）
推导过程：
设r为输入灰度，s为输出灰度
推导文章1 ，推导文章2 ， 推导文章3
视频讲解
最后得到：
上式表明，当T（r）为累计直方图函数时，可以实现直方图均衡
上式表明，输出灰度级 s k s_k sk 可由原直方图的y轴（对应着 r k r_k rk 出现频率）算出
案例：
若想灰度值范围在0~7上， s k s_k sk（横坐标） 乘 7（L-1）
若想纵坐标表示像素个数， p s ( s ) p_s(s) ps(s)（纵坐标） 乘 像素总个数（M*N）
误解
我之前对于归一化有个误解，就是r在[0,7]内，归一到[0,1]间了，其实没有这个规定。归一化只有y轴用p来取代nk的说法。x轴的变换完全是其他人自己假设的。下面是过程：
f S ( s ) = f R ( r ) d r d s 假 设 S 就 是 均 匀 分 布 图 像 ， s 范 围 [ 0 ， L − 1 ] f S ( s ) = 1 L − 1 1 L − 1 d s = f R ( r ) d r 两 边 同 时 积 分 S = ( L − 1 ) ∫ 0 r f R ( r ) d r f_S(s) = f_R(r) \frac{dr}{ds} \\ 假设S就是均匀分布图像，s范围[0，L-1] \\ f_S(s) =\frac{1}{L-1} \\ \frac{1}{L-1} ds = f_R(r)dr \\两边同时积分 \\ S = (L-1)\int_{0}^{r} f_R(r) dr fS(s)=fR(r)dsdr假设S就是均匀分布图像，s范围[0，L−1]fS(s)=L−11L−11ds=fR(r)dr两边同时积分S=(L−1)∫0rfR(r)dr 推导的时候，我把p改成了f，毕竟是概率密度函数，用p看着不舒服
r ∈ [ 0 , L − 1 ] ; p ( r ) 是 概 率 ∈ [ 0 , 1 ] ; s k = ∑ i = 0 k p ( r i ) , 就 是 概 率 的 累 加 ∈ [ 0 , 1 ] ; ( L − 1 ) s k ∈ [ 0 , L − 1 ] r\in[0,L-1]; p(r)是概率\in[0,1]; s_k=\sum_{i=0}^{k} p(r_i),就是概率的累加\in[0,1] ; (L-1)s_k \in [0, L-1] r∈[0,L−1];p(r)是概率∈[0,1];sk=∑i=0kp(ri),就是概率的累加∈[0,1];(L−1)sk∈[0,L−1]
结果表明，直方图均衡化方法并不能生成平坦的直方图（因为假设是连续的，实际是离散的），但它具有能增强图像灰度级的动态范围的特性。