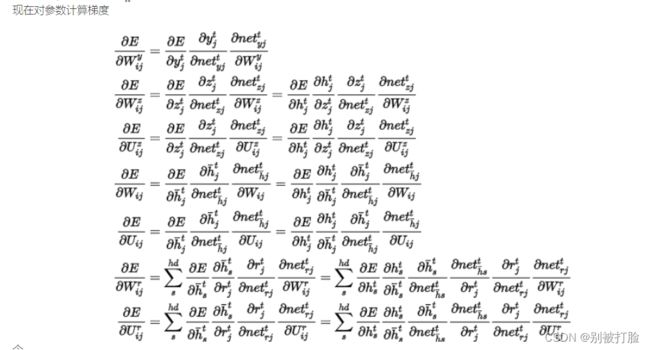NNDL 作业10：第六章课后题（LSTM | GRU）

文章目录

前言

​编辑 一、当使用公式(6.50)作为循环神经网络得状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决办法。

二、习题6-4 推导LSTM网络中参数的梯度，并分析其避免梯度消失的效果

三、习题6-5 推导GRU网络中参数的梯度，并分析其避免梯度消失的效果

四、附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?

五、附加题 6-2P LSTM BP推导，并用Numpy实现

总结

---

前言

      这次，我还是写的很细，并且好多都给出了链接，那些链接真很好，其次是感觉自己太菜了，我是要多学，希望老师和各位大佬多教教我。

      最后希望疫情快点过去吧，我写的不太好，希望老师和各位大佬批评指正。

---

 

 一、当使用公式(6.50)作为循环神经网络得状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决办法。

这个问题，我会给出推导，大家先看一下书上大体的上的描述。

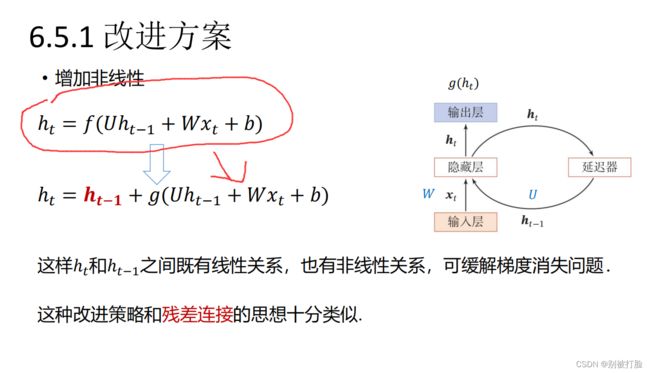
        对公式(6.50),求导可以可以发现，h(t-1)就变成1了，主要引起变化的是后一项，所以，咱们主要研究后一项，也就是g()

        对于g()的研究，大家主要看下边，两张图。

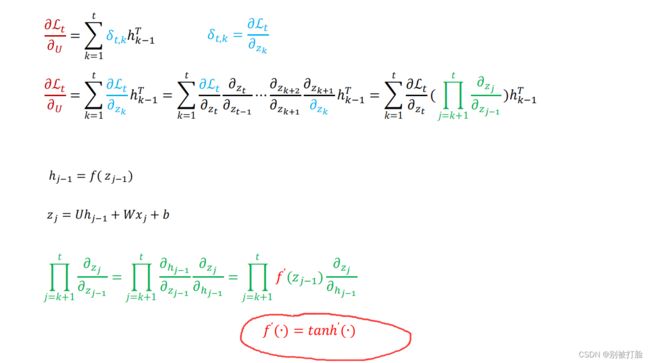
       这张图说明，g()其实就是h()，所以公式(6.30)，在求导上和原来的式子，没有什么较大的区别，所以咱们看一下原来的h()推导。

 

       主要是我圈的这，这是导致梯度爆炸的原因，当层数足够的深的时候，如果tanh的导数小于1还好，要是大于1的话机会导致梯度爆炸的问题了，因为层数足够多的，累乘在一起就会变成很大的数。

        解决办法：加入门控机制来控制信息的累计速度，包括有选择地加入新的信息，并有选择地遗忘之前累积的信息。 就是LSTM网络。

二、习题6-4 推导LSTM网络中参数的梯度，并分析其避免梯度消失的效果

 首先，先放一张，和咱书上结构一样，但是这个把公式都标出来来的图

 然后咱们看一下推导，大家看一下这个链接就明白了

《神经网络的梯度推导与代码验证》之LSTM的前向传播和反向梯度推导 - SumwaiLiu - 博客园

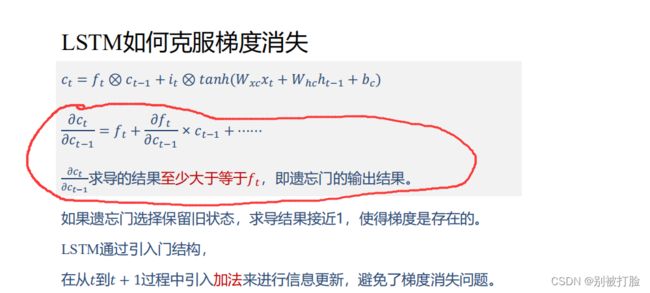
  其中，E是损失函数。

 也就是后边的不用看，只看前边，至少大于等于ft，所以只要保证ft=1，就会缓解梯度消失的问题

三、习题6-5 推导GRU网络中参数的梯度，并分析其避免梯度消失的效果

主要是看这个链接

GRU(Gated Recurrent Unit) 更新过程推导及简单代码实现 - 一只有恒心的小菜鸟 - 博客园

 

 

这个就是下边这张照片了。

四、附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?

看一下这个链接

个人理解关于GRU和LSTM之间的区别和联系_MICSF的博客-CSDN博客_gru与lstm的区别 

人人都能看懂的GRU - 知乎

GRU和LSTM的区别在于：

①GRU通过更新门来控制上一时刻的信息传递和当前时刻计算的隐层信息传递。GRU中由于是一个参数进行控制，因而可以选择完全记住上一时刻而不需要当前计算的隐层值，或者完全选择当前计算的隐层值而忽略上一时刻的所有信息，最后一种情况就是无论是上一时刻的信息还是当前计算的隐层值都选择传递到当前时刻隐层值，只是选择的比重不同。而LSTM是由两个参数（遗忘门和输入门）来控制更新的，他们之间并不想GRU中一样只是由一个参数控制，因而在比重选择方面跟GRU有着很大的区别，例如它可以既不选择上一时刻的信息，也不选择当前计算的隐层值信息（输入门拒绝输入，遗忘门选择遗忘）。

②GRU要在上一时刻的隐层信息的基础上乘上一个重置门，而LSTM无需门来对其控制，LSTM必须考虑上一时刻的隐层信息对当前隐层的影响，而GRU则可选择是否考虑上一时刻的隐层信息对当前时刻的影响。

③ 一般来说两者效果差不多，性能在很多任务上也不分伯仲。GRU参数更少，收敛更快；数据量很大时，LSTM效果会更好一些，因为LSTM参数也比GRU参数多一些。

五、附加题 6-2P LSTM BP推导，并用Numpy实现

这个看一下边这个链接

【手撕LSTM】LSTM的numpy实现_51CTO博客_lstm实现

 代码为：

import numpy as np
def sigmoid(x):
    return 1/(1+np.exp(-x))

def softmax(x):
    e_x = np.exp(x-np.max(x))# 防溢出
    return e_x/e_x.sum(axis=0)


def LSTM_CELL_Forward(xt, h_prev, C_prev, parameters):
    """
    Arguments:
    xt:时间步“t”处输入的数据 shape(n_x,m)
    h_prev:时间步“t-1”的隐藏状态 shape(n_h,m)
    C_prev:时间步“t-1”的memory状态 shape(n_h,m)
    parameters
        Wf 遗忘门的权重矩阵 shape(n_h,n_h+n_x)
        bf 遗忘门的偏置 shape(n_h,1)
        Wi 输入门的权重矩阵 shape(n_h,n_h+n_x)
        bi 输入门的偏置 shape(n_h,1)
        Wc 第一个“tanh”的权重矩阵 shape（n_h，n_h+n_x）
        bc 第一个“tanh”的偏差 shape（n_h，1）
        Wo 输出门的权重矩阵 shape（n_h，n_h+n_x）
        bo 输出门的偏置 shape（n_h，1）
        Wy 将隐藏状态与输出关联的权重矩阵 shape（n_y，n_h）
        by 隐藏状态与输出相关的偏置 shape（n_y，1）
    Returns:
    h_next -- 下一个隐藏状态 shape（n_h，m）
    c_next -- 下一个memory状态 shape（n_h，m）
    yt_pred -- 时间步长“t”的预测 shape（n_y，m）
    """
    # 获取参数字典中各个参数
    Wf = parameters["Wf"]
    bf = parameters["bf"]
    Wi = parameters["Wi"]
    bi = parameters["bi"]
    Wc = parameters["Wc"]
    bc = parameters["bc"]
    Wo = parameters["Wo"]
    bo = parameters["bo"]
    Wy = parameters["Wy"]
    by = parameters["by"]

    # 获取 xt 和 Wy 的维度参数
    n_x, m = xt.shape
    n_y, n_h = Wy.shape

    # 拼接 h_prev 和 xt
    concat = np.zeros((n_x + n_h, m))
    concat[: n_h, :] = h_prev
    concat[n_h:, :] = xt

    # 计算遗忘门、输入门、记忆细胞候选值、下一时间步的记忆细胞、输出门和下一时间步的隐状态值
    ft = sigmoid(np.dot(Wf, concat) + bf)
    it = sigmoid(np.dot(Wi, concat) + bi)
    cct = np.tanh(np.dot(Wc, concat) + bc)
    c_next = ft * C_prev + it * cct
    ot = sigmoid(np.dot(Wo, concat) + bo)
    h_next = ot * np.tanh(c_next)

    # LSTM单元的计算预测
    yt_pred = softmax(np.dot(Wy, h_next) + by)

    return h_next, c_next, yt_pred
np.random.seed(1)
xt = np.random.randn(3,10)
h_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

h_next, c_next, yt = LSTM_CELL_Forward(xt, h_prev, c_prev, parameters)
print("a_next[4] = ", h_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)

运行结果为：

a_next[4] =  [-0.66408471  0.0036921   0.02088357  0.22834167 -0.85575339  0.00138482
  0.76566531  0.34631421 -0.00215674  0.43827275]
a_next.shape =  (5, 10)
c_next[2] =  [ 0.63267805  1.00570849  0.35504474  0.20690913 -1.64566718  0.11832942
  0.76449811 -0.0981561  -0.74348425 -0.26810932]
c_next.shape =  (5, 10)
yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
 0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape =  (2, 10) 

---

总结

          这次真的有点累，推了好多公式，深深地感觉自己太菜了，我还是要多学习，加油。

          其次，是感觉这次看了好多东西之后有点清楚了，感觉真的学了不少东西。

          其次，疫情快过去吧，我回老家之后，也被隔离了，这几天真的有点忙。

          最后，当然是谢谢老师，谢谢老师在学习和生活上的关心(哈哈哈)。