最优化理论笔记及期末复习（《数值最优化》——高立）

一、预备知识

二、无约束最优化方法的基本结构

三、凸集和凸函数

四、负梯度方法和Newton型方法

五、共轭梯度法

六、约束最优化问题的最优性理论

七、罚函数方法

八、期末复习

8.1 知识点复习

8.2 习题复习

8.3 大实验代码

8.3.1实验内容

利用Matlab编程，实现采用简单Armijo非精确线搜索求步长的三种方法：负梯度法、BFGS法及FR共轭梯度法，并求解如下无约束优化问题：
$$minf(x)=10(x_1^3-x_2{)}^2+(x_1-1{)}^2$$
通过实验过程进一步理解三种方法的原理和步骤，并对实验结果进行分析比较。

8.3.2实验目的

掌握无约束最优化算法的基本架构，并能熟练使用Matlab软件实现一些基本实用的算法并进行数值试验分析。

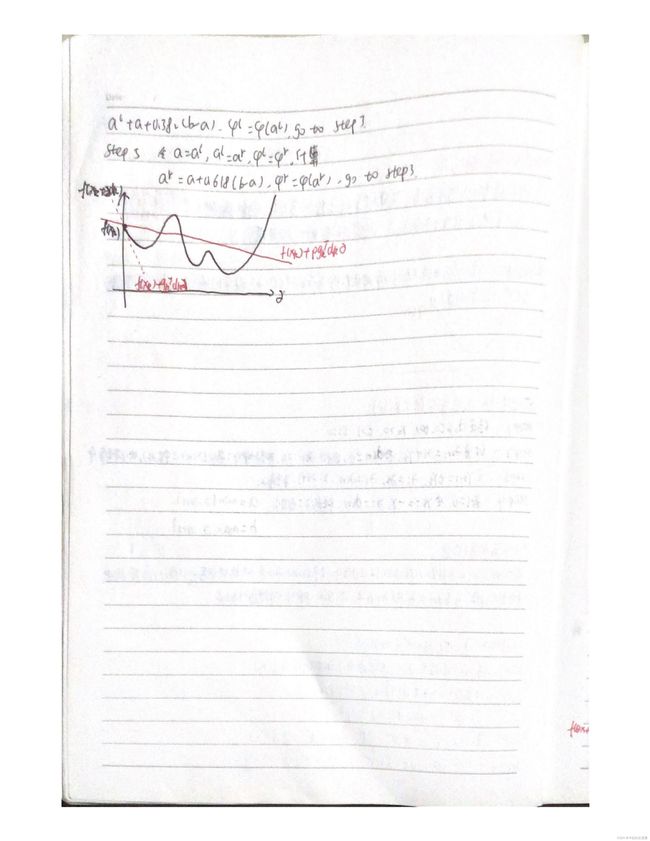
8.3.3算法描述

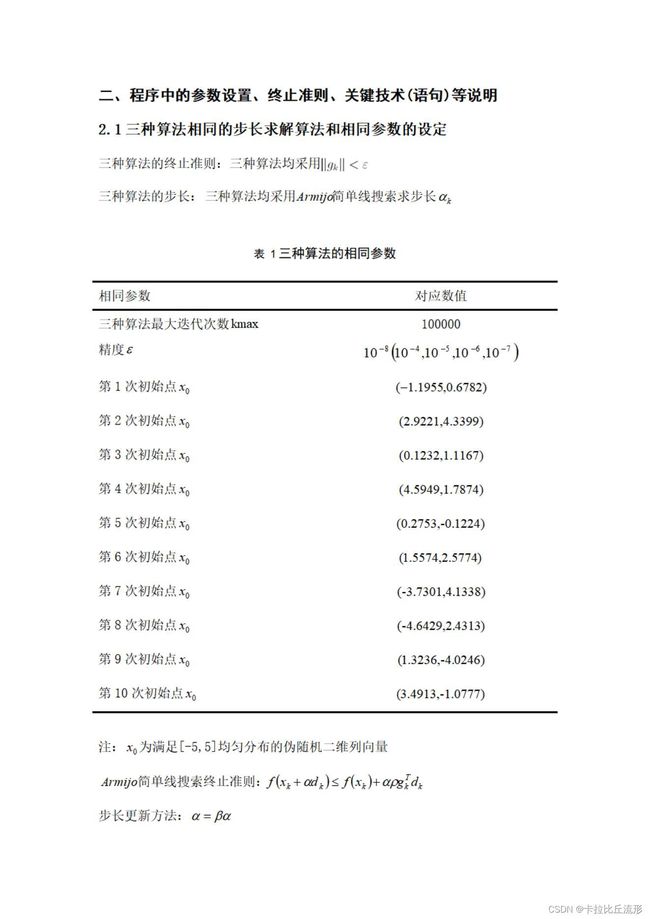
8.3.4程序中的参数设置、终止准则、关键技术(语句)等说明

8.3.5实验代码

8.3.5.1 目标函数

%%计算函数值
function f=func(X)
f=10.*(X(1).^3-X(2)).^2+(X(1)-1).^2;
end

8.3.5.2 计算梯度

%计算梯度值
function g=grd(X)
%计算梯度表达式
% syms x1 x2;
% f=10*(x1^3-x2)^2+(x1-1)^2;
% diff(f,x1)
% diff(f,x2)
% ans = 2*x1 - 60*x1^2*(- x1^3 + x2) - 2
% ans = - 20*x1^3 + 20*x2
g=[2*X(1) - 60*X(1).^2*(- X(1).^3 + X(2)) - 2;- 20*X(1).^3 + 20*X(2)];
end

8.3.5.3 Armijo准则更新步长

function x=armijo(func,xk,dk,gk)
m=0;max_m=1000;
rho=0.001;alpha=1;belta=0.618;
gd=gk'*dk;
fk=feval(func,xk);%初始化条件
while m<max_m
    x=xk+alpha*dk;%试探点
    f=feval(func,x);%试探点的函数值
    if f<=fk+alpha*rho*gd%终止条件
        break;
    end
    alpha=alpha*belta;%修改alpha的值
    m=m+1;
end

8.3.5.4最速下降法

function [x1 fval1 k1]=fd(x0,func,gfunc,eps,kmax)
k1 = 0;
x1 = x0;%设置初始条件
while k1 < kmax
    g = feval(gfunc,x1);%计算梯度，x改变时更新梯度
    if norm(g)<eps%迭代终止条件
        break;
    end
    d=-g;%更新方向
    x1=armijo(func,x1,d,g);%采用Armijo搜索计算当前点x，最终找到近似最优解
    k1=k1+1;
end
fval1=feval(func,x1);%计算目标函数值

8.3.5.5 BFGS法

function [x2,fval2,k2]=bfgs(x0,func,grd,H0,eps,kmax)
k2=0;
H=H0;
x2=x0;
g=feval(grd,x2);%设置初始条件
while k2<kmax
    if norm(g)<eps%终止条件
        break;
    end
    d=-H*g;%更新方向
    x_=x2;%原来的x
    x2=armijo(func,x2,d,g);%更新后的x
    g_=g;%原来的g
    g=feval(grd, x2);%更新后的梯度
    s=x2-x_;
    y=g-g_;
    if s'*y>0
        v=y'*s;
        H=H+(1+(y'*H*y)/v)*(s*s')/v-(s*y'*H+H*y*s')/v;
        %采用BFGS方法更新H
    end
    k2=k2+1;
end
fval2=feval(func,x2);%计算目标函数值

8.3.5.6 FR共轭梯度法

function [x3,fval3,k3]=FR(x0,func,gfunc,eps,kmax)
n=9;k3=0;x3=x0;%设置初始条件
while k3<kmax
    g=feval(gfunc,x3);%更新g
    m=g'*g;%更新后的g*g
    if norm(g)<eps%终止条件
        break;
    end
    if mod(k3,n)==0%n步重新开始策略
        d=-g;
    else
        belta=m/q;%belta的计算
        d=-g+belta*d;%更新d的值
        if g'*d>=0
            d=-g;
        end
    end
    x3=armijo(func,x3,d,g);%采用Armijo搜索计算当前点，最终找到近似最优解
    q=g'*g;%更新前的g*g
    k3=k3+1;
end
fval3=feval(func,x3);%计算目标函数值

8.3.5.7 主程序

clear;clc
x0=unifrnd(-5,5,2,1);%产生满足[-5, 5]均匀分布的初始点
%x0=[3.4913;-1.0777];%[-5,5]均匀分布产生的初始点
...x0=[0.2753;-0.1224];x0=[0.1232;1.1167];x0=[-1.1955;0.6782];x0=[-3.7301;4.1338];x0=[1.3236;-4.0246];
...x0=[2.9221;4.3399];x0=[4.5949;1.7874];x0=[1.5574;2.5774];x0=[-4.6429;2.4313];x0=[3.4913;-1.0777]
eps=1.e-8;%设置精度1.e-4,1.e-5;1.e-6;1.e-7;1.e-8;
kmax=100000;%设置迭代上限
H0=eye(2);%H初始为一个2×2的单位矩阵
%%采用Armijo搜索的负梯度法程序
tic
[x1,fval1,k1]=fd(x0,'func','grd',eps,kmax);
t1=toc;
%%采用Armijo搜索的BFGS法程序
tic
[x2,fval2,k2]=bfgs(x0,'func','grd',H0,eps,kmax)
t2=toc;
%%采用Armijo搜索的FR共轭梯度法程序
tic
[x3,fval3,k3]=FR(x0,'func','grd',eps,kmax);
t3=toc;

SSE1=sqrt(sum((x1-[1;1]).^2,1));%负梯度法下近似解与精确解的2范数下的误差
SSE2=sqrt(sum((x2-[1;1]).^2,1));%BFGS法下近似解与精确解的2范数下的误差
SSE3=sqrt(sum((x3-[1;1]).^2,1));%FR共轭梯度法下近似解与精确解的2范数下的误差
A=[SSE1 fval1 k1 t1;SSE2 fval2 k2 t2;SSE3 fval3 k3 t3]'%分别记录【误差，函数值，迭代次数，运行时间】

九、总结

本篇文章详细的讲解最优化理论的一些常见方法，有了这些基础的最优化知识，方便我们以后深入学习最优化理论以及人工智能方面的知识。