翻译：GloVe: Global Vectors forWord Representation

摘要：最近学习单词的向量空间表示（vector space representations of words）的方法已成功地使用向量算法（vector arithmetic）捕获细粒度的语义（fine-grained semantic）和句法规则（syntactic regularities ），但这些规则的起源仍然是不透明的（opaque）。 我们分析并明确了（explicit）在单词向量中出现这种规则性所需的模型属性（model properties）。结果是一个新的全局logbilinear回归模型，它结合了文献中两个主要模型族的优点：全局矩阵分解（global matrix factorization）和局部上下文窗口方法（local context window methods）。 我们的模型通过仅训练单词 - 单词共生矩阵（cooccurrence matrix）中的非零元素而不是整个稀疏矩阵（entire sparse matrix）或大型语料库（a large corpus）中的各个上下文窗口来有效地利用（leverages）统计（statistical ）信息。该模型产生一个具有有意义子结构（meaningful substructure）的向量空间，其最近一个单词类比任务（word analogy task）的性能为75％。 它在相似性任务（similarity tasks）和命名实体识别（named entity recognition）方面也优于相关模型。

1 Introduction（简介）

语言的语义向量空间模型（Semantic vector space models）用实值向量表示每个单词。 这些向量可以用作各种应用中的特征，例如信息检索（information retrieval）（Manning等，2008），文档分类（document classification）（Sebastiani，2002），问题回答（question answering）（Tellex等，2003），命名实体识别（named entity recognition）（Turian） et al，2010）和解析（Socher et al，2013）。

大多数单词向量方法（Most word vector methods）依赖于单词向量（pairs of word vectors）对之间的距离或角度（angle ），作为评估这样一组单词表示的内在质量（intrinsic quality）的主要方法。 最近，Mikolov等人。 （2013c）引入了一种基于单词类比（word analogies）的新评估方案（evaluation scheme），通过检查单词向量之间的标量距离（ scalar distance），而不是它们各种不同的差异，探讨（probes）单词向量空间的更精细结构（the finer structure）。

例如，类比“国王是女王，男人是女人”应该在向量空间中由向量方程式王 - 女王=男人 - 女人编码（be encoded in）。 该评估方案（This evaluation scheme）倾向于（favors ）产生意义维度（dimensions of meaning）的模型，从而捕获（thereby capturing）分布式表示的多聚类（multi-clustering）思想（Bengio，2009）。

学习单词向量（learning word vectors）的两个主要模型族（model families）是：**1）全局矩阵分解方法（global matrix factorization），如潜在语义分析（ latent semantic analysis–LSA）（Deerwester等，1990）和2）**局部上下文窗口方法（local context window methods），如skip-gram模型 Mikolov等（2013c）。 目前，两类模型方法（both families）都有明显的缺点（ significant drawbacks）。 虽然像LSA这样的方法有效地利用（efficiently leverage）了统计信息，但它们对类比任务（word analogy task）这个词的表现相对较差（relatively poorly），表明了次优的向量空间结构（ sub-optimal vector space structure）。 像skip-gram这样的方法在类比任务（word analogy task）上可能做得更好，但是它们很难利用（ poorly utilize）语料库的统计数据（the statistics of the corpus），因为它们在单独的本地上下文窗口（local context windows）而不是在全局共现计数（global co-occurrence counts）上进行训练。

在这项工作中，我们分析了产生线性方向意义（linear directions of meaning）所必需的模型属性（model properties necessary），并认为（argue that）全局对数双线性回归模型（global log-bilinear regression models）适合这样做（are appropriate for doing so）。 我们提出了一种特定的加权最小二乘模型（specific weighted least squares model），该模型训练全局词 - 词共现计数（global word-word co-occurrence counts），从而有效地利用统计数据（makes efficient use of statistics）。 该模型产生一个具有有意义子结构的单词向量空间（a word vector space with meaningful substructure），其最先进的性能（state-of-the-art）是对单词类比数据集的75％准确性所证明（as evidenced by）。 我们还证明了（demonstrate ）我们的方法在几个单词相似性任务上（word similarity tasks）以及通用的命名实体识别（common named entity recognition-NER）基准上优于（outperform）其他当前方法（other current methods）。我们在http://nlp.stanford.edu/projects/glove/上提供了模型的源代码以及训练过的单词向量。

2 Related Work（相关工作）

矩阵分解方法（Matrix Factorization Methods）。 用于生成低维字表示（generating low-dimensional word representations）的矩阵分解方法可以追溯到LSA。 这些方法利用低秩近似（utilize low-rank approximations）来分解（decompose ）捕获关于语料库的统计信息（statistical information about a corpus）的大矩阵。 由这些矩阵捕获的特定类型的信息因应用而异。在LSA中，矩阵是“术语 - 文档”类型，即，行对应于单词或术语，并且列对应于语料库中的不同文档。 相反（In contrast），例如，语言的超空间模拟（the Hyperspace Analogue to Language）（HAL）（Lund和Burgess，1996）利用“术语 - 术语”类型的矩阵，即行和列对应于单词，而条目对应于单词的次数 给定的单词出现在另一个给定单词的上下文中。

HAL相关方法的一个主要问题是最频繁的单词对相似性度量的贡献不成比例（the most frequent words contribute a disproportionate amount to the similarity measure）：例如，the和and，他们的语义相关性相对较少（semantic relatedness），但the与or共同出现的次数很多。 存在许多解决（addresses）HAL的这种缺点的技术，例如COALS方法（Rohde等人，2006），其中共生矩阵（ co-occurrence matrix）首先通过基于熵或相关的归一化来变换（entropy or correlation-based normalization）。这种类型的变换的优点在于，对于可能跨越8或9个数量级的合理大小的语料库的（which for a reasonably sized corpus might span 8 or 9 orders of magnitude）原始共现计数（raw co-occurrence counts）被压缩，以便在更小的间隔中（a smaller interval）更均匀地分布。 各种新模型也采用这种方法（pursue this approach），包括一项研究（Bullinaria和Levy，2007），表明积极的逐点互信息（PPMI）是一个很好的转变。 最近，Hellinger PCA（HPCA）形式的平方根类型转换（Lebret和Collobert，2014）已被建议作为学习单词表示（ learning word representations）的有效方式。

基于浅窗的方法（Shallow Window-Based Methods）。 另一种方法是学习有助于在本地上下文窗口中进行预测的单词表示。 例如，Bengio等人。 （2003）引入了一个模型，学习单词矢量表示作为语言建模的简单神经网络体系结构的一部分。 Collobert和Weston（2008）将矢量训练一词与下游训练目标分离，这为Collobert等人铺平了道路（paved the way）。 （2011）使用单词的完整（full context of a word）上下文来学习单词表示，而不仅仅是前面的上下文，就像语言模型一样。

最近，用于学习有用的单词表示的完整神经网络结构（full neural network structure）的重要性已经受到质疑（called into question）。 Mikolov等人的skip-gram和连续词袋（CBOW）模型。 （2013a）提出了一种基于两个词向量之间的内积的简单单层架构。 Mnih和Kavukcuoglu（2013）也提出了密切相关的矢量对数 - 双线性模型，vLBL和ivLBL，以及Levy等。 （2014）提出了基于PPMI度量的显式单词嵌入。

在skip-gram和ivLBL模型中，目标是在给定单词本身的情况下预测单词的上下文，而CBOW和vLBL模型中的目标是在给定其上下文的情况下预测单词。 通过对单词类比任务（analogy task）的评估，这些模型展示了（demonstrated）将语言模式（linguistic patterns ）学习为单词向量之间的线性关系的能力。

与矩阵分解方法不同，基于浅窗口的方法的缺点在于它们不直接对语料库的共现统计进行操作（they do not operate directly on the co-occurrence statistics of the corpus）。 相反，这些模型扫描整个语料库（corpus）中的上下文窗口，这无法利用数据中的大量重复的信息（which fails to take advantage of the vast amount of repetition in the data）。

3 The GloVe Model（GloVe 模型）

语料库中（corpus）单词出现的统计数据是所有无监督学习单词表示方法的主要信息来源（primary source），虽然现在存在许多这样的方法，如何从这些统计数据产生（meaning）含义，以及生成的单词向量如何表示该（meaning）含义。 在本节中，我们对这个问题有所了解（we shed some light on this question）。 我们使用我们的见解（insights ）构建一个新的单词表示模型（a new model for word representation），我们称之为GloVe，用于全局向量，因为全局语料库统计数据是由模型直接捕获的（the global corpus statistics）。

首先，我们建立一些符号（notation）。 将字 - 词共同出现次数（word-word co-occurrence counts）的矩阵表示为X，其条目$X_{ij}$表示word j出现在单词i的上下文中的次数。 设$X_i={\sum }_k{X}_{ik}$是任何单词出现在单词i的上下文中的次数。 最后，让$P_{ij}=P(j|i)=X_{ij}/X_i$是单词j出现的概率

表1：具有来自60亿 token corpus（就是该语料库含有60亿个词。注：可重复） 的所选上下文词（selected context words）的目标词（target words）ice和steam的共现概率（Co-occurrence probabilities）。 只有在这个比例中，来自water和fashion等非歧视性词语（non-discriminative）的噪音才会抵消（cancel out），因此大的值（远大于1）与ice的特性相关性很好，而小值（远小于1）与特定的属性关系良好steam。

我们从一个简单的例子开始，展示了如何直接从共现概率（occurrence probabilities）中提取意义的某些方面。 考虑两个表示感兴趣的特定方面的词i和j; 具体而言（for concreteness），假设我们对热力学阶段（thermodynamic phase）的概念感兴趣，我们可以采用i = ice和j = steam。 可以通过研究它们的共现概率（cooccurrence probabilities）与各种探测词（probe words）k的比率（the ratio of their）来检验（examined）这些词的关系。 对于与ice而不是steam相关的单词k，比如说k = solid，我们预计比率$P_{ik}/P_{jk}$会很大。类似地（Similarly），对于与steam而非ice相关的单词k，比如k = gas，该比率应该很小。 对于像ice或fashion这样的词语k，无论是ice与steam，还是两者都不相关，这个比例应该接近1。 表1显示了这些概率及其与大型语料库的比率（ratios），数字证实了这些期望。 与原始概率相比（raw probabilities），该比率能够更好地（is better able to）区分（distinguish）相关词（solid 和 gas）与不相关词（ice和fashion），并且还能够更好地区分（discriminate）两个相关词。

上述论点表明（The above argument suggests that），单词向量学习的适当起点（appropriate starting point）应该是共现概率的比率（ ratios of co-occurrence probabilities）而不是概率本身（probabilities themselves）。 注意到比率$P_{ik}/P_{jk}$取决于三个单词i，j和k，最通用的模型采用的形式，

其中$w\in {\mathbb{R}}^d$是单词向量，$w\in {\mathbb{R}}^d$是单独的上下文单词向量，其作用将在4.2节中讨论。在该等式中，右侧（right-hand side）是从语料库（corpus）中提取的，并且F可以取决于一些尚未指定（as-of-yet unspecified）的参数。 F的可能性很大（The number of possibilities for F is vast），但通过强制执行一些需求（desiderata ），我们可以选择一个独特的选择。 首先，我们希望F对在字向量空间中呈现比率$P_{ik}/P_{jk}$的信息进行编码。 由于向量空间本质上是线性结构（inherently linear structures），因此最自然的方法是使用向量差异（vector differences）。有了这个目标，我们可以将我们的考虑限制在仅依赖于两个目标词的差异（the difference of the two target words），修改Eqn的那些函数F. （1）到，

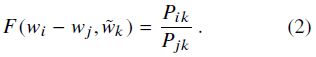
接下来，我们注意到公式（2）中的F的参数是向量，而右侧（right-hand side）是标量（scalar）。 虽然F可以被认为是由例如神经网络参数化的复杂函数（complicated function parameterized），但是这样做会混淆（obfuscate）我们试图捕获的线性结构。 为了避免这个问题，我们可以先拿参数的点积（dot product），

这可以防止F以不希望（undesirable ）的方式混合矢量尺寸。 接下来，请注意（note that），对于单词共现矩阵，单词和上下文单词之间的区别是任意的，我们可以自由地交换这两个角色。为了这样做的一致性（To do so
consistently），我们不仅要交换$w\leftrightarrow w$，同时也要交换$X\leftrightarrow X^T$。我们的最终模型在这种重新标记下（relabeling）应该是不变的（invariant），但是Eqn（3）不是。 但是，对称性（symmetry）可以分两步恢复（restored）。首先，我们要求F是群$(\mathbb{R},+)$和$({\mathbb{R}}_{>0},\times )$之间的同态（homomorphism）

其中，由Eqn（3），解决了，

公式（4）的解是F=exp，也就是

接下来，我们注意到公式（6）如果不是右侧的$log(X_i)$，则表现出交换对称性（exhibit the exchange symmetry）。 然而，该项与k无关，因此它可以被吸收到$w_i$的偏置$b_i$中。 最后，为$w_k$添加额外的偏差$b_k$可以恢复对称性（restores the symmetry），

公式（7）是对公式（1）的极大简化。 但它实际上是不明确的（it is actually ill-defined），因为只要参数（argument）为零，对数（logarithm）就会发散（diverges）。该问题的一个解决方案（resolution ）是在对数中包括加性偏移（additive shift）$log(X_{ik})\to log(1+X_{ik})$，它保持了X的稀疏性（sparsity of X），同时避免了分歧（divergences）。将共生矩阵（ co-occurrence matrix ）的对数分解（factorizing the log）的想法与LSA密切相关，我们将使用得到的模型作为我们实验中的基线（baseline）。 这种模式的一个主要缺点（A main drawback）是，它平等地权衡所有共现（it weighs all co-occurrences equally），甚至是那些很少或从未发生的共现。 这种罕见的共现是嘈杂（noisy）的，并且信息比较频繁的信息少 - 但即使只有零条目（zero entries）占X中数据的75-95％，这取决于词汇量（vocabulary size）和语料库（corpus）。

我们提出了一种新的加权最小二乘回归模型（weighted least squares regression model）来解决这些问题（addresses these problems）。 将公式（7）作为最小二乘问题（least squares problem）并将加权函数$f(X_{ij})$引入到成本函数中给出了模型

其中V是词汇量的大小（the size of the vocabulary）。 加权函数应遵循以下属性（The weighting
function should obey the following properties）：

• $f(x)=0$。如果$f$被视为连续的函数，f应该随着$x\to 0$而趋于0，并且有$li{m}_{x\to 0}f(x)lo{g}^{2}x$趋于无穷。
• f（x）应该是非递减的，以便罕见（rare）的共现（co-occurrences）不会超重（overweighted）。
• 对于较大的x值，f（x）应该相对较小，因此频繁的（frequent）共现不会超重（overweighted）。

当然，大量函数满足（satisfy ）这些属性，但我们发现可以很好地工作的一类函数可以参数化为，

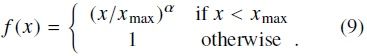
The performance of the model depends weakly on the cutoff，我们所有的实验都设定$x_{max}=100$ 我们发现$\alpha$= 3/4比使用$\alpha$= 1的线性版本提供了适度的改进（modest improvement）。虽然我们仅提供选择3/4值的经验动机（empirical motivation），但有趣的是，发现类似的分数功率缩放（fractional power scaling）以提供最佳性能（best performance）。（Mikolov等，2013a）。