【论文翻译】A Global Geometric Framework for Nonlinear Dimensionality Reduction

论文题目：A Global Geometric Framework for Nonlinear Dimensionality Reduction
论文来源：Science 290, 2319 (2000);

A Global Geometric Framework for Nonlinear Dimensionality Reduction

Joshua B. Tenenbaum,1* Vin de Silva,2John C. Langford3

Abstract

Scientists working with large volumes of high-dimensional data, such as global climate patterns, stellar spectra, or human gene distributions, regularly confront the problem of dimensionality reduction: finding meaningful low-dimensional structures hidden in their high-dimensional observations. The human brain confronts the same problem in everyday perception, extracting from its high-dimensional sensory inputs—30,000 auditory nerve fibers or 106optic nerve fibers—a manageably small number of perceptually relevant features. Here we describe an approach to solving dimensionality reduction problems that uses easily measured local metric information to learn the underlying global geometry of a data set. Unlike classical techniques such as principal component analysis (PCA) and multidimensional scaling (MDS), our approach is capable of discovering the nonlinear degrees of freedom that underlie complex natural observations, such as human handwriting or images of a face under different viewing conditions. In contrast to previous algorithms for nonlinear dimensionality reduction,ours efficiently computes a globally optimal solution, and, for an important class of data manifolds, is guaranteed to converge asymptotically to the true structure.

摘要

科学家在处理大量高维数据（例如全球气候模式，恒星光谱或人类基因分布）时，经常会遇到降维问题：在高维观测中发现有意义的低维结构。人脑在日常感知中面临着同样的问题，它从其高维感官输入中提取了3万听觉神经纤维或106视神经纤维，这是数量很少的感知相关特征。在这里，我们描述了一种解决降维问题的方法，该方法使用易于测量的局部度量信息来学习数据集的基础全局几何。与经典技术（例如主成分分析（PCA）和多维缩放（MDS））不同，我们的方法能够发现非线性的自由度，这些自由度是复杂自然观察的基础，例如在不同的观察条件下的人类笔迹或脸部图像。与以前的非线性降维算法相比，我们有效地计算了全局最优解，并且对于一类重要的数据流形，可以保证渐近收敛到真实结构。

正文

A canonical problem in dimensionality re-duction from the domain of visual perception is illustrated in Fig. 1A. The input consists of many images of a person’s face observed under different pose and lighting conditions, in no particular order. These images can be thought of as points in a high-dimensional vector space, with each input dimension cor- responding to the brightness of one pixel in the image or the firing rate of one retinal ganglion cell. Although the input dimension-ality may be quite high (e.g., 4096 for these 64 pixel by 64 pixel images), the perceptually meaningful structure of these images has many fewer independent degrees of freedom. Within the 4096-dimensional input space, all of the images lie on an intrinsically three- dimensional manifold, or constraint surface, that can be parameterized by two pose vari- ables plus an azimuthal lighting angle. Our goal is to discover, given only the unordered high-dimensional inputs, low-dimensional representations such as Fig. 1A with coordi- nates that capture the intrinsic degrees of freedom of a data set. This problem is of central importance not only in studies of vi- sion (1–5), but also in speech (6, 7 ), motor control (8, 9), and a range of other physical and biological sciences (10–12).
在图1A中说明了从视觉领域降维的典型问题。输入包括在不同姿势和光照条件下观察到的许多人脸图像，没有特定的顺序。这些图像可以看作是高维向量空间中的点，每个输入维对应于图像中一个像素的亮度或一个视网膜神经节细胞的放电速率。尽管输入维数可能相当高（例如，对于这些64像素×64像素图像，为4096），但是这些图像的感知意义结构具有更少的独立自由度。在4096维输入空间内，所有图像都位于一个本质上三维流形或约束曲面上，该流形可以通过两个姿态变量和一个方位照明角度进行参数化。我们的目标是发现仅给出无序的高维输入的低维表示形式，如图1A所示，其坐标捕获了数据集的固有自由度。这个问题不仅在视觉的研究中非常重要，而且在语言，运动控制和一系列其他物理和生物科学中也是至关重要的。

The classical techniques for dimensional- ity reduction, PCA and MDS, are simple to implement, efficiently computable, and guar- anteed to discover the true structure of data lying on or near a linear subspace of the high-dimensional input space (13). PCA finds a low-dimensional embedding of the data points that best preserves their variance as measured in the high-dimensional input space. Classical MDS finds an embedding that preserves the interpoint distances, equiv- alent to PCA when those distances are Eu- clidean. However, many data sets contain essential nonlinear structures that are invisible to PCA and MDS (4, 5, 11, 14 ). For example, both methods fail to detect the true degrees of freedom of the face data set (Fig. 1A), or even its intrinsic three-dimensionality (Fig. 2A).
经典的降维技术，PCA和MDS，实现简单，可高效计算，并保证发现位于高维输入空间的线性子空间上或附近的数据的真实结构。PCA找到一个低维的数据点嵌入，可以最好地保持在高维输入空间中测量到的方差。经典的MDS发现了一种嵌入，该嵌入保留了点间距离，当这些距离为欧几里得时，其等效于PCA。然而，许多数据集包含基本的非线性结构，这些结构对PCA和MDS是不可见的。例如，两种方法都无法检测出人脸数据集的真实自由度(图1A)，甚至无法检测出人脸数据集的固有三维度(图2A)。

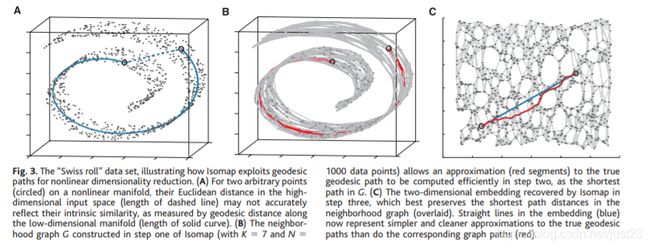
Here we describe an approach that combines the major algorithmic features of PCA and MDS—computational efficiency, global optimality, and asymptotic convergence guarantees—with the flexibility to learn a broad class of nonlinear manifolds. Figure 3A illus- trates the challenge of nonlinearity with data lying on a two-dimensional “Swiss roll”: points far apart on the underlying manifold, as mea- sured by their geodesic, or shortest path, dis- tances, may appear deceptively close in the high-dimensional input space, as measured by their straight-line Euclidean distance. Only the geodesic distances reflect the true low-dimensional geometry of the manifold, but PCA and MDS effectively see just the Euclidean struc- ture; thus, they fail to detect the intrinsic two- dimensionality (Fig. 2B).
在这里，我们描述了一种结合了PCA和MDS的主要算法功能（计算效率，全局最优性和渐近收敛性保证）的方法，该方法可以灵活地学习各种非线性流形。图3A说明了数据位于二维“瑞士卷”上时的非线性挑战：在基础流形上相距很远的点（通过测地线或最短路径的距离来衡量）在高维输入空间中可能看起来很近，以它们的直线欧几里得距离来衡量。只有测地距离反映流形的真实低维几何，但是PCA和MDS只有效地看到了欧几里德结构；因此，它们无法检测到内在的二维性（图2B）。

Our approach builds on classical MDS but seeks to preserve the intrinsic geometry of the data, as captured in the geodesic manifold distances between all pairs of data points. The crux is estimating the geodesic distance between faraway points, given only input-space distances. For neighboring points, input- space distance provides a good approximation to geodesic distance. For faraway points, geodesic distance can be approximated by adding up a sequence of “short hops” between neighboring points. These approximations are computed efficiently by finding shortest paths in a graph with edges connecting neighboring data points.
我们的方法建立在经典MDS的基础上，但是试图保留数据的内在几何结构，正如在所有对数据点之间的测地流形距离中捕捉到的那样。问题的关键是在给定输入空间距离的情况下，估计远距离点之间的测地距离。对于相邻点，输入空间距离可以很好地近似测地距离。 对于较远的点，可以通过将相邻点之间的“短跳”序列相加来近似测地距离。 这些近似值可以通过在图中找到具有连接相邻数据点的边的最短路径来有效地计算。

The complete isometric feature mapping, or Isomap, algorithm has three steps, which are detailed in Table 1. The first step determines which points are neighbors on the manifold M, based on the distances dX (i, j) between pairs of points i, j in the input space X. Two simple methods are to connect each point to all points within some fixed radius E, or to all of its K nearest neighbors (15). These neighborhood relations are represented as a weighted graph G over the data points, with edges of weight dX(i, j) between neighboring points (Fig. 3B).
完整的等距特征映射算法或Isomap算法包括三个步骤，如表1所示。第一步根据输入空间X中两对点i，j之间的距离dX（i，j）确定流形M上哪些点是相邻点。两种简单的方法是将每个点连接到某个固定半径E内的所有点，或连接到其所有K个最近邻点。这些邻域关系表示为数据点上的加权图G，相邻点之间的权重dX（i，j）的边缘（图3B）。

In its second step, Isomap estimates the geodesic distances dM (i, j) between all pairs of points on the manifold M by computing their shortest path distances dG (i, j) in the graph G. One simple algorithm (16 ) for finding shortest paths is given in Table 1.
在第二步中，Isomap通过计算流形M上所有点对之间的最短路径距离dG（i，j）来估计流形M上所有点对之间的测地距离dM（i，j）。表1给出了一个求最短路径的简单算法。

The final step applies classical MDS to the matrix of graph distances DG = {d_G(i,j)}, constructing an embedding of the data in a d-dimensional Euclidean space Y that best preserves the manifold’s estimated intrinsic geometry (Fig. 3C). The coordinate vectors yi for points in Y are chosen to minimize the cost function
$E=||\tau (D_G)-\tau (D_Y)|{|}_{{}^{L^2}}$ (1)
where $D_Y$ denotes the matrix of Euclidean distances {{d_Y(i,j) = ||y_i -y_j||} and $||A|{|}_L{}^2$the L² matrix norm $\sqrt{{\sum }_{i,j}{A}_{i,j}^2}$ . The τ operator converts distances to inner products (17), which uniquely characterize the geometry of the data in a form that supports efficient optimization. The global minimum of Eq. 1 is achieved by setting the coordinates yi to the top d eigenvectors of the matrix τ(D_G)(13).
最后一步将经典MDS应用于图距离DG = {d_G(i,j)}的矩阵，在d维欧几里德空间Y中构造数据的嵌入，该空间最好地保持流形估计的内在几何结构（图3C）。选择Y点的坐标向量$y_i$来最小化代价函数。
$E=||\tau (D_G)-\tau (D_Y)|{|}_{{}^{L^2}}$ (1)
其中$D_Y$表示欧几里得距离矩阵{{d_Y(i,j) = ||y_i -y_j||}，而$||A|{|}_L{}^2$是L² 矩阵范数$\sqrt{{\sum }_{i,j}{A}_{i,j}^2}$ 。 T运算符将距离转换为内部乘积，该乘积以支持有效优化的形式唯一地表征数据的几何形状。公式1的全局最小值是通过将坐标$y_i$设置为矩阵 τ(D_G)的顶部d特征向量来实现的。

As with PCA or MDS, the true dimensionality of the data can be estimated from the decrease in error as the dimensionality of Y is increased. For the Swiss roll, where classical methods fail, the residual variance of Isomap correctly bottoms out at d = 2 (Fig. 2B).
与PCA或MDS一样，数据的真实维数可以通过Y维数增加时误差的减小来估计。对于瑞士卷，在经典方法失败的情况下，Isomap的残差在d=2时正确地触底（图2B）。

Just as PCA and MDS are guaranteed, given sufficient data, to recover the true structure of linear manifolds, Isomap is guaranteed asymptotically to recover the true dimensionality and geometric structure of a strictly larger class of nonlinear manifolds. Like the Swiss roll, these are manifolds
就像有足够的数据可以保证PCA和MDS恢复线性流形的真实结构一样，Isomap被保证渐近地恢复一类严格更大的非线性流形的真实维数和几何结构,这些就像瑞士卷一样都是流形的。

whose intrinsic geometry is that of a convex region of Euclidean space, but whose ambient geometry in the high-dimensional input space may be highly folded, twisted, or curved. For non-Euclidean manifolds, such as a hemisphere or the surface of a doughnut, Isomap still produces a globally optimal low- dimensional Euclidean representation, as measured by Eq. 1.
其内在几何形状是欧几里得空间的凸区域，但是其高维输入空间中的周围几何形状可能会高度折叠，扭曲或弯曲。 对于非欧氏流形，例如半球或甜甜圈的表面，Isomap仍会生成一个全局最优的低维欧氏表示，如等式1所测量。

These guarantees of asymptotic convergence rest on a proof that as the number of data points increases, the graph distances $d_G\left(i,j\right)$provide increasingly better approximations to the intrinsic geodesic distances $d_M\left(i,j\right)$, becoming arbitrarily accurate in the limit of infinite data (18, 19). How quickly $d_G\left(i,j\right)$ converges to $d_M\left(i,j\right)$ depends on certain parameters of the manifold as it lies within the high-dimensional space (radius of curvature and branch separation) and on the density of points. To the extent that a data set presents extreme values of these parameters or deviates from a uniform density, asymptotic convergence still holds in general, but the sample size required to estimate geodesic distance accurately may be impractically large.
渐近收敛的这些保证基于以下证明：随着数据点数量的增加，图距离$d_G\left(i,j\right)$提供了与内在测地距离$d_M\left(i,j\right)$越来越接近的近似值，在无限数据的极限下变得任意精确。$d_G\left(i,j\right)$收敛到$d_M\left(i,j\right)$的速度取决于流形位于高维空间（曲率半径和分支分离）中的某些参数和点的密度,如果一组数据呈现出这些参数的极值或偏离均匀密度，一般来说，渐近收敛仍然成立，但精确估计测地线距离所需的样本容量可能不切实际地大。

Isomap’s global coordinates provide a simple way to analyze and manipulate high- dimensional observations in terms of their intrinsic nonlinear degrees of freedom. For a set of synthetic face images, known to have three degrees of freedom, Isomap correctly detects the dimensionality (Fig. 2A) and separates out the true underlying factors (Fig. 1A). The algorithm also recovers the known low-dimensional structure of a set of noisy real images, generated by a human hand varying in finger extension and wrist rotation (Fig. 2C) (20). Given a more complex data set of handwritten digits, which does not have a clear manifold geometry, Isomap still finds globally meaningful coordinates (Fig. 1B) and nonlinear structure that PCA or MDS do not detect (Fig. 2D). For all three data sets, the natural appearance of linear interpolations between distant points in the low-dimensional coordinate space confirms that Isomap has captured the data’s perceptually relevant structure (Fig. 4).
Isomap的全局坐标提供了一种根据其内在的非线性自由度来分析和处理高维观测值的简单方法。对于已知具有三个自由度的一组合成人脸图像，Isomap可以正确检测到维度（图2A）并分离出真正的潜在因素（图1A）。对于已知具有三个自由度的一组合成人脸图像，Isomap可以正确检测到维度（图2A）并分离出真正的潜在因素（图1A）。该算法还恢复了一组嘈杂的真实图像的已知低维结构，该图像是由人的手在手指伸展和手腕旋转中变化而产生的（图2C）。给定更复杂的手写数字数据集（没有清晰的流形几何），Isomap仍然可以找到全局有意义的坐标（图1B）和PCA或MDS无法检测到的非线性结构（图2D）。对于所有三个数据集，低维坐标空间中远距离点之间的线性插值的自然出现证实了Isomap已经捕捉到数据的感知相关结构（图4）

Previous attempts to extend PCA and MDS to nonlinear data sets fall into two broad classes, each of which suffers from limitations overcome by our approach. Local linear techniques (21–23) are not designed to represent the global structure of a data set within a single coordinate system, as we do in Fig. 1. Nonlinear techniques based on greedy optimization procedures (24–30) attempt to discover global structure, but lack the crucial algorithmic features that Isomap inherits from PCA and MDS: a noniterative, polynomial time procedure with a guarantee of global optimality; for intrinsically Euclidean manifolds, a guarantee of asymptotic convergence to the true structure; and the ability to discover manifolds of arbitrary dimensionality, rather than requiring a fixed d initialized from the beginning or computational resources that increase exponentially in d.
先前尝试将PCA和MDS分为两大类扩展到非线性数据集，我们的方法克服了每一类的局限性。局部线性技术并不像我们在图1中所做的那样，被设计用于在单个坐标系中表示数据集的全局结构。基于贪婪优化程序的非线性技术试图发现全局结构，但缺乏Isomap从PCA和MDS继承的关键算法特征：一种保证全局最优性的非迭代多项式时间过程；对于本质上的欧几里德流形，渐近收敛到真实结构的保证；以及发现任意维数流形的能力，而不需要从一开始就初始化一个固定的d或在d中呈指数增长的计算资源。

Here we have demonstrated Isomap’s performance on data sets chosen for their visually compelling structures, but the technique may be applied wherever nonlinear geometry complicates the use of PCA or MDS. Isomap complements, and may be combined with, linear extensions of PCA based on higher order statistics, such as independent component analysis (31, 32). It may also lead to a better understanding of how the brain comes to represent the dynamic appearance of objects, where psychophysical studies of apparent motion (33, 34 ) suggest a central role for geodesic transformations on nonlinear manifolds (35) much like those studied here.
在这里，我们演示了Isomap在数据集上的性能，这些数据集是根据其视觉上引人注目的结构选择的，但该技术可以应用于任何非线性几何使PCA或MDS的使用复杂化的地方。Isomap是对基于高阶统计量的PCA的线性扩展的补充，并可能与之结合，如独立分量分析。它也可能有助于更好地理解大脑是如何表现物体的动态外观的，其中表观运动的心理物理学研究表明，在非线性流形上的测地线变换起着核心作用，就像这里研究的那些。