2022-3-21至2022-3-27周报
文章目录
- 摘要
- 文献阅读
-
- 一 Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting
- 1论文摘要
- 2论文研究内容
- 3创新点
-
- 金字塔注意模块(PAM)
- 粗尺度构建模型(CSCM)
- 预测模块
- 消融实验
- 4作者的研究思路或研究方法
- 5用哪些数据来论证的
- 基础知识
-
- Full-Attention
- Transformer
-
- Transformer架构
- 多头注意力(Multi-head attention)
- 有掩码的多头注意力(Masked multi-head attention)
- 基于位置的前馈网络(Positionwise FFN)
- 层归一化(Add & norm)
- 信息传递
- 预测
- 小结
- 带毕设
- 展望
摘要
一、本周文献部分将上篇文章读完,并阅读文章附录,理解其中树形结构相关的粗尺度能够提取全局特征等数学公式的证明。
二、基础知识部分,理解transformer是带有attention机制的一种encoder-decoder模型,并学习其特有的一些细节。
文献阅读
一 Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting
- 会议:ICLR
- 作者及单位:Shizhan Liu, Hang Yu, Cong Liao, Jianguo Li, Weiyao Lin, Alex X. Liu, Schahram Dustdar;上海交通大学,南洋理工大学,蚂蚁集团;
1论文摘要
我们通过探索时间序列的多分辨率表示,提出了Pyraformer。Pyraformer引入金字塔注意模块,该模块采用inter-scale树结构,来提取不同分辨率下的特征;采用intra-scale邻居连接模型,对不同范围的时间依赖关系进行建模,来捕捉时间序列预测中的长期依赖关系。结果能做到线性的时间和空间复杂度,并实现信号遍历路径的最大长度是常数。
2论文研究内容
时序预测的主要挑战在于:构建一个强大但简洁的模型,可以紧凑地捕捉不同范围的时间相关性。时间序列通常表现出短期和长期的时间相关性,考虑到它们是准确预测的关键。处理长期依赖关系的难度更大,因为长期依赖关系的特点是:时间序列中任意两点之间最长的信号穿越路径的长度。路径越短,相关性捕获越好。为了让模型了解这些长期相关性,模型的历史输入也应该很长。因此,低的时间和空间复杂度是优先考虑的问题。
时序预测可以表述为,给出过去的L步观测值 z t − L + 1 : t z_{t-L+1:t} zt−L+1:t和相关协变量 x t − L + 1 : t + M x_{t-L+1:t+M} xt−L+1:t+M,预测未来M步 z t + 1 : t + M z_{t+1:t+M} zt+1:t+M
3创新点
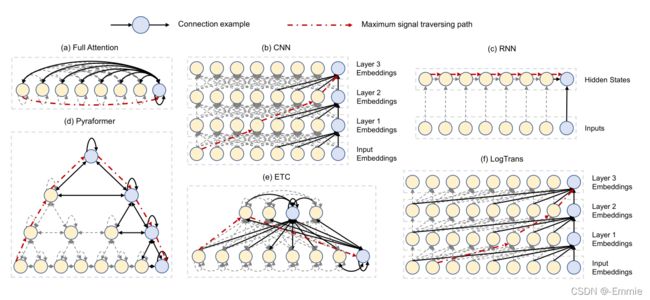
图中(d)为本文提出的金字塔模型,采用树结构,在边中传递基于注意力的信息,图中有两种类型的边:
- 尺度间连接(inter-scale):构建了原始序列的多分辨率表示。最细尺度上的节点对应于原始时间序列中的时间点(如每小时、每4小时);粗尺度上的节点则代表分辨率较低的特征(如每天、每周和每月的自相关性)。使用粗尺度构建模块提取较粗尺度节点的初始状态。
- 内部尺度(intra-scale)的边通过将相邻节点连接在一起,来捕获每个分辨率上的时间相关性。
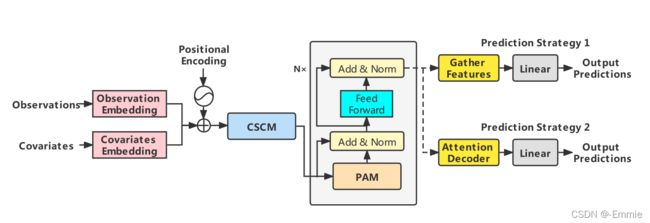
图为Pyraformer模型的结构。
首先将观察值、协变量和位置分别输入,并将它们相加,相加的结果输入到粗尺度构建模型(CSCM)中。CSCM是一个多分辨率C叉树,较粗尺度上的节点总结了相应较细尺度上C个节点的信息。其次,引入金字塔注意模块(PAM),利用金字塔图中的注意力机制传递信息。最后,根据下游任务的不同,我们使用不同的网络结构来输出最终的预测。
金字塔注意模块(PAM)
尺度间的连接形成一个C-ary树,树的每个父结点都有C子结点。【C有两种确定方法:第一种,C可视为超参数,后面给出C需要满足的条件。第二种,C从7,12这样的数中选择,其含义是尺度相关的,小时、周等等】
设最细尺度节点为小时观测值,则较粗尺度节点可视为日特征,甚至月特征。因此,金字塔图提供了原时间序列的多分辨率表示。将相邻节点通过尺度内连接连接起来,更容易在粗尺度上捕获长期依赖关系。
不同于full attention mechanism,每个节点只计算有限的矩阵点积, n l ( s ) n^{(s)}_l nl(s)表示在s尺度上第 l l l个节点,其中 s = 1 , . . . , S s=1,...,S s=1,...,S,每个节点只注意3个尺度的邻居节点集 N l ( s ) N^{(s)}_l Nl(s):
- 相邻节点在同一尺度的(包括节点本身) A l ( s ) A^{(s)}_l Al(s)
- C个子节点的尺度 C l ( s ) C^{(s)}_l Cl(s)
- 父节点的尺度 P l ( s ) P^{(s)}_l Pl(s)
各个集合:
- N l ( s ) = A l ( s ) ⋃ C l ( s ) ⋃ P l ( s ) N^{(s)}_l=A^{(s)}_l\bigcup C^{(s)}_l\bigcup P^{(s)}_l Nl(s)=Al(s)⋃Cl(s)⋃Pl(s)
- A l ( s ) = { n l ( s ) : ∣ j − l ∣ ⩽ ( A − 1 ) / 2 , 1 ⩽ j ⩽ L / C S − 1 } A^{(s)}_l=\{ n^{(s)}_l : |j-l| \leqslant (A-1)/2 , 1\leqslant j \leqslant L/C^{S-1}\} Al(s)={nl(s):∣j−l∣⩽(A−1)/2,1⩽j⩽L/CS−1}
- C l ( s ) = { n l ( s − 1 ) : l ⩽ j ⩽ l C } C^{(s)}_l=\{ n^{(s-1)}_l : l \leqslant j \leqslant lC \} Cl(s)={nl(s−1):l⩽j⩽lC} i f s ⩾ 2 e l s e ∅ if s \geqslant 2 else \emptyset ifs⩾2else∅
- P l ( s ) = { n l ( s + 1 ) : ⌈ l / C ⌉ } P^{(s)}_l=\{ n^{(s+1)}_l : \lceil l/C \rceil \} Pl(s)={nl(s+1):⌈l/C⌉} i f s ⩽ S − 1 e l s e ∅ if s \leqslant S-1 else \emptyset ifs⩽S−1else∅
为不失一般性,假设 L ∣ C S − 1 L|C^{S-1} L∣CS−1
定义:
- 注意力层数为N
- L表示历史序列或输入时间序列的长度
- A表示一个节点可以处理的相同尺度相邻节点的数量
引理1:
N层注意力层之后,满足下式,最粗尺度的节点可以获得全局的接受域
L / C S − 1 − 1 ⩽ ( A − 1 ) N / 2 L/C^{S-1} -1\leqslant (A-1)N/2 L/CS−1−1⩽(A−1)N/2
命题1:
给定A和L,Pyraformer的时间和空间复杂度为 O ( A L ) O(AL) O(AL),且当A是关于L的常数时,复杂度相当于 O ( L ) O(L) O(L)
命题2:
给定A,C,L和S,两个任意节点间信号穿越路径的最大长度为 O ( S + L / C S − 1 ∗ A ) O(S+L/C^{S-1}* A) O(S+L/CS−1∗A)
且当A和S固定,C满足下式时,对长为L的时间序列,最大路径长度为 O ( 1 ) O(1) O(1)
L S − 1 ⩾ C ⩾ L / ( A − 1 ) N / 2 + 1 S − 1 \sqrt[S-1]{L}\geqslant C\geqslant \sqrt[S-1]{L/(A-1)N/2+1} S−1L⩾C⩾S−1L/(A−1)N/2+1
注:信号穿越路径指图中两点之间的最短距离
实验中,固定S和N,A只能取3或5。在PAM中,一个节点最多能注意A+C+1个节点。使用TVM为PAM构建了一个定制的CUDA内核,减少计算时间和内存成本,才免于时空复杂度为 O ( L 2 ) O(L^2) O(L2)【如果不这么实现,做常规的矩阵运算复杂度仍为 O ( L 2 ) O(L^2) O(L2)】
粗尺度构建模型(CSCM)
对对应的子节点 C l ( s ) C^{(s)}_l Cl(s)进行卷积,从下到上逐级引入粗尺度节点,在时间维上对嵌入序列依次施加核大小为C、步长为C的几个卷积层,得到尺度为S、长度为 L / C S L/C^S L/CS的序列。得到不同尺度的序列构成C叉树。将这些序列拼接起来再输入PAM中。
预测模块
1single-step forecasting:
在历史序列 z t − L + 1 : t z_{t-L+1:t} zt−L+1:t的结尾加一个结束标记 z t + 1 = 0 z_{t+1}=0 zt+1=0。在PAM编码后,将金字塔图中所有尺度上最后一个节点给出的特征收集起来,拼接后输入到全连接层中进行预测。
2multi-step forecasting
提出2个预测模块,第一个与单步预测模块相同,但将所有尺度上的最后一个节点批量映射到所有M个未来时间步长。
第二个模块借助于一个有两层注意力的解码器,做原Transformer的变体:将未来M个时间步长的观测值替换为0,按照与历史观测值相同的方式进行嵌入,并将观测值、协变量和位置嵌入的和作为“预测标记” F p F_p Fp。第一个注意力层将 F p F_p Fp视为query,将encoder的输出 F e F_e Fe视为key和value,产生 F d 1 F_{d1} Fd1。第二个注意力层将 F d 1 F_{d1} Fd1作为query,将 拼接后的 F d 1 F_{d1} Fd1 和 F e F_e Fe作为key和value。历史信息 F e F_e Fe直接输入两个注意力层,然后通过跨通道维度的完全连接层获得最终预测。输出所有的特征预测。
消融实验
实验数据表明模型的各个模块的表现以及它们的作用。
4作者的研究思路或研究方法
目前SOTA模型不能既具有低的时间和空间复杂度,又具有小的最长信号遍历路径。
两个极端模型,一端是RNN和CNN,在时间序列长为L时,实现线性时间复杂度,最长信号穿越路径为 O ( L ) O(L) O(L),使得远距离的两点之间的相关性很难挖掘。另一端是Transformer,时间复杂度为 O ( L 2 ) O(L^2) O(L2),最长信号穿越路径为 O ( 1 ) O(1) O(1),故不能处理长序列。
为了平衡时间复杂度和最长信号穿越路径,一些Transformer的变体:Longformer、Reformer、Informer被提出,而很少有算法能实现既保持低的时间复杂度,又实现最长信号遍历路径小于 O ( L ) O(L) O(L)
5用哪些数据来论证的
四个真实世界中的数据集,Wind、App Flow和Electricity用于单步预测,Electricity和ETT用于长时间范围内的多步预测。
单步预测的历史序列的长度分别为169、192和192,将Paraformer与the original full-attention, the log-sparse attention, the LSH attention, the sliding window attention with global nodes(如ETC)和the dilated sliding window(如Longformer)这五个模型进行比较评估。为了进行公平的比较,除了full-attention外,所有注意力机制的整体点积数量被控制在相同的数量级。评估参数数量、NRMSE、ND和query-key点积的数量。
长时间范围的多步预测同时预测未来油温和6个电力负荷特性,时间序列长度从96到720不等,均能以最少的query-key点积的数量得到最佳的效果。
(为了进行公平的比较,除了full-attention外,所有的注意力机制的变体的整体点积数量被控制在相同的数量级。
基础知识
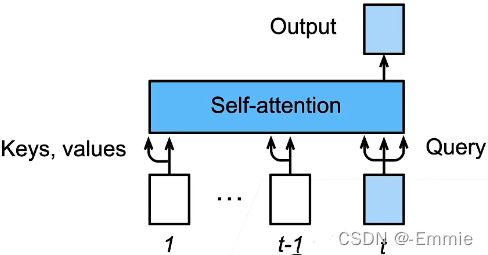
Full-Attention
设X和Y代表一个单头注意力的输入和输出,可以引入多头注意力来从不同的角度描述时间相关性。
X先线性变换成三个不同的矩阵,
- query Q = X W Q Q=XW_Q Q=XWQ
- key K = X W K K=XW_K K=XWK
- value V = X W v V=XW_v V=XWv
其中 W Q , W K , W V ∈ R L ∗ D k W_Q,W_K,W_V\in R_{L*D_k} WQ,WK,WV∈RL∗Dk
Q中的第i行可以处理K中的任何行(计算时K转置)
需要计算和存储的query-key点积的数量决定了注意力机制的时间和空间复杂度。点积的数量和结构图中边的数量成比例。
Transformer
Transformer架构
- 基于 编码器-解码器(Encoder-Decoder) 架构来处理序列对
- 跟使用注意力的seq2seq不同, Transformer是纯基于注意力,或者说它是一种纯基于Self-Attention的架构
seq2seq架构:

Transformer架构:
多头注意力(Multi-head attention)就是一个Self-Attention,Positionwise FNN就是全连接。

多头注意力(Multi-head attention)
- 对同一key,value,query,希望抽取不同的信息
例如短距离和长距离关系。 - 多头注意力使用 h 个独立的注意力池化
合并各个头(head)输出得到最终输出。
Multi-head attention架构:

用数学语言将多头注意力形式化地描述出来。给定 query q ∈ R d q \mathbb{R}^{d_{q}} Rdq,key k ∈ R d k \mathbb{R}^{d_{k}} Rdk,value v ∈ R d v \mathbb{R}^{d_{v}} Rdv ,每个注意力头 h i h_i hi ( i=1 , 2 , … , h ) 的计算方法为:
h i = f ( W i ( q ) q , W i ( k ) k , W i ( v ) v ) ∈ R p v h_i = f(W^{(q)}_iq,W^{(k)}_ik,W^{(v)}_iv) ∈ \mathbb{R}^{p_{v}} hi=f(Wi(q)q,Wi(k)k,Wi(v)v)∈Rpv
其中,头 i 的可学习参数包括 W i ( q ) W^{(q)}_i Wi(q) ∈ R p q × d q \mathbb{R}^{p_{q}×d_{q}} Rpq×dq, W i ( k ) W^{(k)}_i Wi(k) ∈ R p k × d k \mathbb{R}^{p_{k}×d_{k}} Rpk×dk, W i ( v ) W^{(v)}_i Wi(v) ∈ R p v × d v \mathbb{R}^{p_{v}×d_{v}} Rpv×dv ,以及代表注意力汇聚的函数 f f f 。 f f f 可以是加性注意力和缩放点积注意力。多头注意力的输出需要经过另一个线性转换, 它对应着 h 个头连结后的结果,因此其可学习参数是 W o W_o Wo ∈ R p o × h p v \mathbb{R}^{p_{o}×hp_{v}} Rpo×hpv :
W o [ h 1 ⋮ h h ] ∈ R p o W_o \begin{bmatrix} h_1 \\ ⋮ \\ h_h \end{bmatrix} ∈ \mathbb{R}^{p_{o}} Wo⎣⎢⎡h1⋮hh⎦⎥⎤∈Rpo
基于这种设计,每个头都可能会关注输入的不同部分,可以表示比简单加权平均值更复杂的函数。
PyTorch实现
class MultiHeadAttention(nn.Module):
"""多头注意力"""
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = d2l.DotProductAttention(dropout)
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
def forward(self, queries, keys, values, valid_lens):
# queries,keys,values的形状:
# (batch_size,查询或者“键-值”对的个数,num_hiddens)
# valid_lens 的形状:
# (batch_size,)或(batch_size,查询的个数)
# 经过变换后,输出的queries,keys,values 的形状:
# (batch_size*num_heads,查询或者“键-值”对的个数,
# num_hiddens/num_heads)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
if valid_lens is not None:
# 在轴0,将第一项(标量或者矢量)复制num_heads次,
# 然后如此复制第二项,然后诸如此类。
valid_lens = torch.repeat_interleave(
valid_lens, repeats=self.num_heads, dim=0)
# output的形状:(batch_size*num_heads,查询的个数,
# num_hiddens/num_heads)
output = self.attention(queries, keys, values, valid_lens)
# output_concat的形状:(batch_size,查询的个数,num_hiddens)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat)
def transpose_qkv(X, num_heads):
"""为了多注意力头的并行计算而变换形状"""
# 输入X的形状:(batch_size,查询或者“键-值”对的个数,num_hiddens)
# 输出X的形状:(batch_size,查询或者“键-值”对的个数,num_heads,
# num_hiddens/num_heads)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
# 输出X的形状:(batch_size,num_heads,查询或者“键-值”对的个数,
# num_hiddens/num_heads)
X = X.permute(0, 2, 1, 3)
# 最终输出的形状:(batch_size*num_heads,查询或者“键-值”对的个数,
# num_hiddens/num_heads)
return X.reshape(-1, X.shape[2], X.shape[3])
def transpose_output(X, num_heads):
"""逆转transpose_qkv函数的操作"""
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
return X.reshape(X.shape[0], X.shape[1], -1)
# Test
num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
attention.eval()
batch_size, num_queries = 2, 4
num_kvpairs, valid_lens = 6, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
Y = torch.ones((batch_size, num_kvpairs, num_hiddens))attention(X, Y, Y, valid_lens).shape
有掩码的多头注意力(Masked multi-head attention)
- 解码器对序列中一个元素输出时,不应该考虑该元素的之后的元素
Self-Attention可以考虑全局长距离的信息,如果不掩盖的话,就好比预测时已经能看到答案结果。 - 可以通过掩码来实现
也就是计算 x i x_i xi 输出时,假装当前序列长度为 i 。
基于位置的前馈网络(Positionwise FFN)
- 将输入形状由三维的 (b,n,d) 变换成 (bn,d)
b:多少个句子
n:句子有多少个字
d:这个字有多少维 - 作用两个全连接层
- 输出形状由 (bn,d) 变化回 (b,n,d)
- 等价于两层核窗口为1的以为卷积层
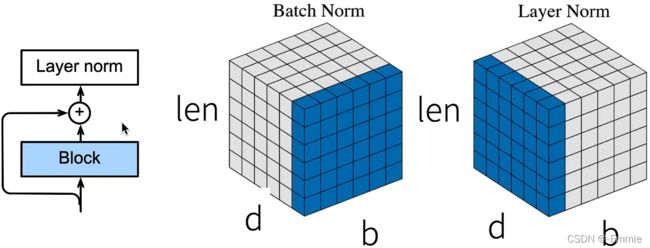
层归一化(Add & norm)
- 批量归一化对每个特征/通道里元素进行归一化
不适合序列长度会变的NLP应用。 - 层归一化对每个样本里的元素进行归一化
把不同句子相同位置的token作为同一个特征进行归一化是不合适的。
信息传递
- 编码器中的输出 y 1 y_1 y1, … , y n y_n yn
- 将其作为解码中第 i 个Transformer块中多头注意力的 key 和 value
它的 query 来自目标序列。 - 意味着编码器和解码器中块的个数和输出维度都是一样的
预测
小结
- Transformer是一个纯使用注意力的编码-解码器
- 编码器和解码器都有n个transformer块
- 每个块里使用多头(自)注意力,基于位置的前馈网络和层归一化
带毕设
催促其写框架,运行项目代码答疑。