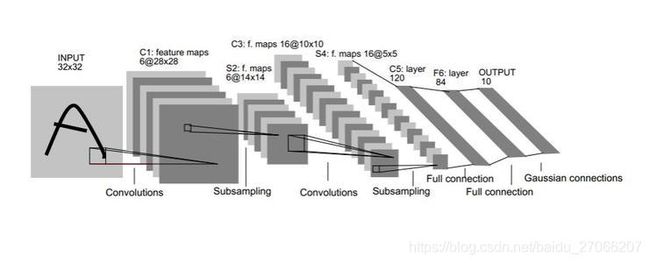
LeNet网络详解与pytorch实现

最近在学习B站一个up主的视频，很棒。故决定在学习过程中进行笔记整理和总结。（无它，自用自勉）

给出收藏的博主笔记及up主笔记，以便自己日后查找翻阅。

• 博主链接-LeNet                     

Pytorch中tensor（输入输出层）的通道排序为：[batch, channel, height, width]

Pytorch中的卷积、池化、输入输出层中参数的含义与位置如下图所示

1. 模型代码model.py

import torch.nn as nn
import torch.nn.functional as F
# torch.nn包用来构建神经网络

class LeNet(nn.Module):                     #定义一个模型，继承于nn.Module父类
    def __init__(self):
        super(LeNet, self).__init__()       # 多继承，调用父类函数
        self.conv1 = nn.Conv2d(3, 16, 5)    # 输入深度，卷积核个数，卷积核尺寸
        self.pool1 = nn.MaxPool2d(2, 2)     # 池化核尺寸为2*2
        self.conv2 = nn.Conv2d(16, 32, 5)
        self.pool2 = nn.MaxPool2d(2, 2)
        self.fc1 = nn.Linear(32*5*5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):       # 输入数据，Tensor
        x = F.relu(self.conv1(x))    # input(3, 32, 32) output(16, 28, 28)
        x = self.pool1(x)            # output(16, 14, 14)
        x = F.relu(self.conv2(x))    # output(32, 10, 10)
        x = self.pool2(x)            # output(32, 5, 5)
        x = x.view(-1, 32*5*5)       # output(32*5*5)   展平操作，-1表示第一维度推理
        x = F.relu(self.fc1(x))      # output(120)
        x = F.relu(self.fc2(x))      # output(84)
        x = self.fc3(x)              # output(10) 
        # 最后一层为什么没有用softmax函数，内部已经有实现
        return x

2. 相关函数解析

2.1 卷积Conv2d()

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0,
  dilation=1, groups=1, bias=True, padding_mode='zeros')

重要参数说明：

• in_channels：输入特征矩阵的深度。
• out_channels：输出特征矩阵的深度，也即卷积核的个数，使用n个卷积核卷积后得到的特征矩阵的深度就是n
• kernel_size：卷积核尺寸大小。（可为int型，如3，表示卷积核大小为3×3，也可为tuple类型，如（3,5）表示卷积核大小为3×5 【height×width】）
• stride：卷积核的步长。默认为1，与kernel_size类似，可为int型，也可为tuple型
• padding：边界填充——补零操作的参数，默认为0。可为int型，如1，表示在矩阵外围补一圈零；也可为tuple型，如(1,2)，1表示上下方各补一行零，2表示左右两侧各补两列零。（更精细化的padding操作-nn.ZeroPad2d((1,2,1,2))表示左侧补一列，右侧补两列，上方补一行，下方补两行）
• dilation(int or tuple, optional)：卷积核元素之间的间距
• groups(int, optional)：控制输入与输出之间的连接。group=1，输出是所有的输入的卷积；group=2，此时相当于有并排的两个卷积层，每个卷积层计算输入通道的一半，并且产生的输出是输出通道的一半，随后将这两个输出连接起来。
• bias(bool, optional)：如果bias=True，添加偏置。

输入图像经卷积后输出图像尺寸的计算公式：

                     

• output：输出图像大小参数
• input：输入图像大小W×H（一般情况下Width=Hieight）
• P：（Padding）在图像边缘增加的边界像素层数
• S：卷积核的步长

学习中视频博主提及，若计算结果不为整数？可参考Pytorch中的卷积操作详解

2.2 局部池化MaxPool2d()

torch.nn.MaxPool2d(kernel_size, stride=None, padding=0,
                                                          dilation=1, return_indices=False, ceil_mode=False)

 重要参数说明：

• kernel_size：池化窗口大小。（一般是[height, width]，若二者相等，可以是一个数字，如kernel_size=3）
• stride：窗口在每一个维度上滑动的步长。（一般是[stride_h, stride_w]，若二者相等，可是一数字，如stride=1）
• padding：与卷积类似
• dilation：
• return_indices：
• ceil_mode：

输入图像经池化后输出图像尺寸的计算公式：

                          

与卷积类似，且输入的特征图的深度与滑动窗口的深度保持一致。

2.3 Tensor展平view()

在经过池化层之后，数据仍为一个三维的Tensor(32,5,5)，需要经过展平(32*5*5)以后才能够传到全连接层。

a = torch.tensor([[1, 2, 3],
                  [4, 5, 6]])
b = torch.tensor([[[1, 2],
                   [3, 4]],
 
                  [[5, 6],
                   [7, 8]],
                   
                  [[9, 0],
                   [11, 12]]])
print(a.view(-1))
print(b.size())
print(b.view(-1))
print(b.view(3, -1))
print(b.view(-1, 2 * 2))

输出：

tensor([1, 2, 3, 4, 5, 6])
torch.Size([3, 2, 2])
tensor([ 1,  2,  3,  4,  5,  6,  7,  8,  9,  0, 11, 12])
tensor([[ 1,  2,  3,  4],
        [ 5,  6,  7,  8],
        [ 9,  0, 11, 12]])
tensor([[ 1,  2,  3,  4],
        [ 5,  6,  7,  8],
        [ 9,  0, 11, 12]])

分析：（-1表示让其自己运算）

对于二维张量a，a.view(-1)直接将二维张量展平为一维张量（对于本身就是一维的张量来说view(-1)没有意义）

对于高维张量，如三维张量（3×2×2）b，如果调用b.view(-1)会将b转换为一维张量；如果调用b.view(3, -1)则会将b转换为3×n维的张量，n取决与b原来的结构由剩下的两个维度（2×2）展平得到；同理b.view(-1, 2 * 2)会将b转换成n×4维的张量。两者的效果是完全一样的 

ps：view函数得到张量示图与原张量共享数据（可以理解为一种引用），而且view只能处理连续的张量，对于不连续的张量（如转置后的张量）则可以用contiguous函数后再用view函数或直接使用reshape函数，reshape函数是对view的改进版，当张量连续是功能和view相同，当张量不连续时则会复制一份同时丧失数据共享。

2.4 全连接层Linear()

Linear(in_features, out_features, bias=True)      #   ，x是输入，A是权值，b是偏置，y是输出

从输入输出的张量的shape角度来理解，相当于一个输入为[batch_size, in_features]的张量变换成了[batch_size, out_features]的输出张量。

参数说明：

in_features：输入的二维张量的大小，即输入的[batch_size, size]中的size。

out_features：输出的二维张量的大小，即输出的二维张量的形状为[batch_size，output_size]，当然，它也代表了该全连接层的神经元个数。

bias： Default： “True”，偏置，默认有偏置

注意：全连接层的输入与输出都是二维张量，一般形状为[batch_size, size]，不同于卷积层要求输入输出是四维张量

3. 训练代码train.py

import torch
import torchvision
import torch.nn as nn
from model import LeNet
import torch.optim as optim
import torchvision.transforms as transforms
import time
import numpy as np
import matplotlib.pyplot as plt

def main():
    # 对输入的图像数据做预处理
    # 即由shape (H x W x C) in the range [0, 255] → shape (C x H x W) in the range [0.0, 1.0]
    transform = transforms.Compose(
        [transforms.ToTensor(),
         transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

    # 50000张训练图片
    # 第一次使用时要将download设置为True才会自动去下载数据集
    train_set = torchvision.datasets.CIFAR10(root='./data', # 数据集存放目录
                                             train=True,    # 表示是数据集中的训练集
                                             download=True, # 第一次运行时为True，去自动下载数据集，下载完成后改为False
                                             transform=transform) # 预处理过程
    # 加载训练集，实际过程需要分批次（batch）训练
    train_loader = torch.utils.data.DataLoader(train_set,       # 导入的训练集
                                               batch_size=36,   # 每批训练的样本数
                                               shuffle=True,    # 是否随机打乱数据集
                                               num_workers=0)   # 使用线程数，在windows下设置为0

    # 10000张验证图片
    # 第一次使用时要将download设置为True才会自动去下载数据集
    val_set = torchvision.datasets.CIFAR10(root='./data', train=False,  # 表示是数据集中的验证集
                                           download=False, transform=transform)
    val_loader = torch.utils.data.DataLoader(val_set, batch_size=5000,  # 每批用于验证的样本数量
                                             shuffle=False, num_workers=0)
    # 获取测试集中的图像和标签，用于accuracy计算
    val_data_iter = iter(val_loader)
    val_image, val_label = val_data_iter.next()

    classes = ('plane', 'car', 'bird', 'cat',
               'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

    # def imshow(img):
    #     img = img/2+0.5    # unnormalize，反标准化还原回去
    #     npimg = img.numpy()
    #     plt.imshow(np.transpose(npimg, (1,2,0))) # C,H,W ——>H,W,C
    #     plt.show()

    net = LeNet()                                       # 定义训练所用的网络模型
    loss_function = nn.CrossEntropyLoss()               # 定义损失函数（这里为交叉熵损失函数）
    optimizer = optim.Adam(net.parameters(), lr=0.001)  # 定义优化器（训练参数，学习率）

    for epoch in range(5):  # loop over the dataset multiple times
        # 一个epoch即对整个训练集进行一次训练
        running_loss = 0.0
        time_start = time.perf_counter()

        # 遍历训练集，step从0开始计算
        for step, data in enumerate(train_loader, start=0):
            # get the inputs; data is a list of [inputs, labels]
            inputs, labels = data   # 获取训练集的图像和标签
            # zero the parameter gradients
            optimizer.zero_grad()   # 历史梯度清零
            # forward + backward + optimize
            outputs = net(inputs)                   # 正向传播
            loss = loss_function(outputs, labels)   # 计算损失
            loss.backward()                         # 反向传播
            optimizer.step()                        # 迭代更新参数

            # print statistics（打印耗时、损失、准确率等数据信息）
            running_loss += loss.item()
            if step % 500 == 499:    # print every 500 mini-batches（每500步打印一次）
                with torch.no_grad(): # with是一个上下文管理器
                    # 在这个函数的计算内，都不会改变梯度，即不用计算每个节点的误差损失梯度，防止占用内存及运算资源
                    outputs = net(val_image)  # [batch, 10]测试集传入网络
                    predict_y = torch.max(outputs, dim=1)[1] # 以output中值最大位置（在第一维度）对应的索引（标签）作为预测输出
                    accuracy = torch.eq(predict_y, val_label).sum().item() / val_label.size(0)

                    # 打印epoch，step，loss，accuracy
                    print('[%d, %5d] train_loss: %.3f  test_accuracy: %.3f' %
                          (epoch + 1, step + 1, running_loss / 500, accuracy))
                    # 打印耗时
                    print('%f s' %(time.perf_counter()-time_start))
                    running_loss = 0.0

    print('Finished Training')

    # 保存训练得到的参数模型
    save_path = './Lenet.pth'
    torch.save(net.state_dict(), save_path)

if __name__ == '__main__':
    main()

4. 预测代码predict.py

import torch
import torchvision.transforms as transforms
from PIL import Image
from model import LeNet

def main():
    transform = transforms.Compose(
        [transforms.Resize((32, 32)),  # 首先需将数据集resize成与训练集图像一样的大小
         transforms.ToTensor(),
         transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

    classes = ('plane', 'car', 'bird', 'cat',
               'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

    # 实例化网络
    net = LeNet()
    # 用下述函数载入刚刚训练好的网络模型
    net.load_state_dict(torch.load('Lenet.pth'))

    # 导入要测试的图像，用PIL载入
    im = Image.open('1.jpg')
    im = transform(im)  # [C, H, W]
    # 对数据增加一个新维度，因为tensor的参数是[batch, channel, height, width]
    im = torch.unsqueeze(im, dim=0)  # [N, C, H, W]

    with torch.no_grad():
        outputs = net(im)
        predict = torch.max(outputs, dim=1)[1].data.numpy()
        # 预测结果也可用softmax，输出十个概率，输出结果中最大概率值对应的索引即为预测标签的索引
        # predict = torch.softmax(outputs, dim=1)
    print(classes[int(predict)])


if __name__ == '__main__':
    main()