机器学习入门-西瓜书总结笔记第六章
西瓜书第六章-支持向量机
- 一、间隔与支持向量
- 二、对偶问题
- 三、核函数
- 四、软间隔与正则化
- 五、支持向量回归
- 六、核方法
- 总结
一、间隔与支持向量
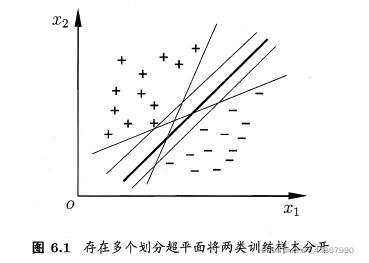 粗实线这个划分超平面所产生的分类结果是最鲁棒的,对未来示例的泛化能力最强
粗实线这个划分超平面所产生的分类结果是最鲁棒的,对未来示例的泛化能力最强
在样本空间中,划分超平面可通过如下线性方程来描述:
w T x + b = 0 , \pmb w^T\pmb x +b =0, wwwTxxx+b=0,
其中 w = ( w 1 ; w 2 ; ⋯ ; w d ) \pmb w =(w_1;w_2;\cdots;w_d) www=(w1;w2;⋯;wd)为法向量,决定超平面的方向;b为位移项,决定了超平面与原点之间的距离
样本空间中任意点 x \pmb x xxx到超平面 ( w , b ) (\pmb w,b) (www,b)的距离可写为
r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ r=\frac{ |\pmb w^T \pmb x +b|}{||\pmb w||} r=∣∣www∣∣∣wwwTxxx+b∣
{ w T x i + b ≥ + 1 , y i = + 1 w T x i + b ≤ − 1 , y i = − 1 \begin{cases} \pmb w^T \pmb x_i +b \geq +1, \quad y_i=+1\\ \pmb w^T \pmb x_i +b \leq -1, \quad y_i=-1 \end{cases} {wwwTxxxi+b≥+1,yi=+1wwwTxxxi+b≤−1,yi=−1
距离超平面最近的这几个训练样本点使上式的等号成立,它们被称为 “支持向量”(support vector),两个异类支持向量到超平面的距离之和为
γ = 2 ∣ ∣ w ∣ ∣ \gamma = \frac{2}{||\pmb w||} γ=∣∣www∣∣2
它被称为 “间隔”(margin)
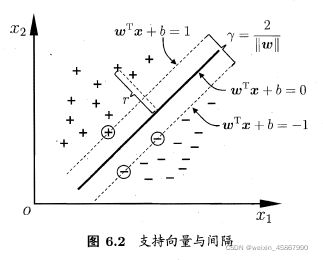 欲找到具有“最大间隔”(maximum margin)的划分超平面,就是要找到能满足约束的参数 w \pmb w www和 b b b,使得 γ \gamma γ最大,即
欲找到具有“最大间隔”(maximum margin)的划分超平面,就是要找到能满足约束的参数 w \pmb w www和 b b b,使得 γ \gamma γ最大,即
max w , b 2 ∣ ∣ w ∣ ∣ s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , ⋯ , m \underset {w,b}{\operatorname {max}} \frac{2}{||\pmb w||}\\ s.t.\quad y_i(\pmb w^T \pmb x_i +b) \geq 1, \quad i=1,2,\cdots,m w,bmax∣∣www∣∣2s.t.yi(wwwTxxxi+b)≥1,i=1,2,⋯,m
可重写为
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , ⋯ , m \underset {w,b}{\operatorname {min}} \frac{1}{2}||\pmb w||^2\\ s.t.\quad y_i(\pmb w^T \pmb x_i +b) \geq 1, \quad i=1,2,\cdots,m w,bmin21∣∣www∣∣2s.t.yi(wwwTxxxi+b)≥1,i=1,2,⋯,m
这就是支持向量机(Support Vector Machine,简称SVM)的基本型
二、对偶问题
支持向量机的基本型本身是一个 凸二次规划(convex quadratic programming),能直接用现成的优化计算包求解,但其实有更高效的方法
- 对上式使用拉格朗日乘子法可得到其 “对偶问题”(dual problem) ,具体来说,对每条约束添加拉格朗日乘子 a i ≥ 0 a_i \geq 0 ai≥0,则该问题的拉格朗日函数可写为
L ( w , b , a ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m a i ( 1 − y i ( w T x i + b ) ) , L(\pmb w,b ,\pmb a)=\frac{1}{2}||\pmb w||^2 + \sum_{i=1}^m a_i(1-y_i(\pmb w^T\pmb x_i +b)), L(www,b,aaa)=21∣∣www∣∣2+i=1∑mai(1−yi(wwwTxxxi+b)),
其中 a = ( a 1 ; a 2 ; ⋯ ; a m ) \pmb a=(a_1;a_2;\cdots;a_m) aaa=(a1;a2;⋯;am),对 w \pmb w www和 b b b求偏导为0
w = ∑ i = 1 m a i y i x i 0 = ∑ i = 1 m a i y i \pmb w = \sum_{i=1}^m a_i y_i \pmb x_i\\ 0=\sum_{i=1}^ma_iy_i www=i=1∑maiyixxxi0=i=1∑maiyi
即可将 L ( w , b , a ) L(\pmb w,b ,\pmb a) L(www,b,aaa)中消去 w \pmb w www和 b b b,再考虑约束,就得到它的对偶问题
max a ∑ i = 1 m a i − 1 2 ∑ i = 1 m ∑ j = 1 m a i a j y i y j x i T x j s . t . ∑ i = 1 m a i y i = 0 a i ≥ 0 , i = 1 , 2 , ⋯ , m \underset {\pmb a}{\operatorname {max}} \sum_{i=1}^m a_i -\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m a_i a_j y_i y_j \pmb x_i^T\pmb x_j\\ s.t. \sum_{i=1}^m a_iy_i=0\\ a_i \geq 0 ,\quad i=1,2,\cdots,m aaamaxi=1∑mai−21i=1∑mj=1∑maiajyiyjxxxiTxxxjs.t.i=1∑maiyi=0ai≥0,i=1,2,⋯,m
解出 a \pmb a aaa后,求出 w \pmb w www和 b b b即可得到模型
f ( x ) = w T x + b = ∑ i = 1 m a i y i x i T x + b \begin{aligned} f(x) &= \pmb w^Tx+b\\ &=\sum_{i=1}^ma_iy_i\pmb x_i^T\pmb x +b \end{aligned} f(x)=wwwTx+b=i=1∑maiyixxxiTxxx+b
支持向量的基本型有不等约束,因此上述过程需满足KKT(Karush-Kuhn-Tucker)条件,即要求
{ a i ≥ 0 ; y i f ( x i ) − 1 ≥ 0 ; a i ( y i f ( x i ) − 1 ) = 0 \begin{cases} a_i \geq 0;\\ y_if(\pmb x_i) - 1 \geq 0;\\ a_i(y_if(\pmb x_i) - 1)=0 \end{cases} ⎩⎪⎨⎪⎧ai≥0;yif(xxxi)−1≥0;ai(yif(xxxi)−1)=0
补充KKT条件资料 - 显示出支持向量机的一个重要性质:训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量相关
- SMO(Sequential Minimal Optimization)节省计算开销,SMO每次选择两个变量 a i a_i ai和 a j a_j aj,并固定其他参数,在参数初始化后,SMO不断执行如下两个步骤直至收敛:1.选取一对需更新的变量 a i a_i ai和 a j a_j aj.2.固定 a i a_i ai和 a j a_j aj以外的参数,求解对偶问题获得更新后的 a i a_i ai和 a j a_j aj
- 直观来看,KKT条件违背的程度越大,则变量更新后可能导致目标函数数值减幅增大。SMO先选取违背KKT条件程度最大的变量,第二个变量应选择一个使目标函数值减小最快的变量(计算复杂度高),SMO采用了一个启发式:使选取的两个变量所对应的样本之间间隔最大,约束可重新写为
a i y i + a j y j = c , a i ≥ 0 , a j ≥ 0 a_iy_i+a_jy_j=c,\quad a_i \geq 0,a_j \geq 0 aiyi+ajyj=c,ai≥0,aj≥0
其中
c = − ∑ k = i , j a k y k c=-\sum_{k=i,j}a_ky_k c=−k=i,j∑akyk
如何确定偏移项 b b b呢?注意到对任意支持想想 ( x s , y s ) (x_s,y_s) (xs,ys)都有 y s f ( x s ) = 1 y_sf(x_s)=1 ysf(xs)=1,即
y s ( ∑ i ∈ S a i y i x i T x s + b ) = 1 y_s(\sum_{i\in S}a_iy_i\pmb x_i^T \pmb x_s +b)=1 ys(i∈S∑aiyixxxiTxxxs+b)=1
理论上可选取任意支持向量并通过求解上式得到 b b b,但现实任务中常采用一种更鲁棒的做法:使用所有支持向量求解的平均值
b = 1 ∣ S ∣ ∑ s ∈ S ( y s − ∑ i ∈ S a i y i x i T x s ) b=\frac{1}{|S|}\sum_{s\in S}(y_s - \sum_{i\in S}a_iy_i\pmb x_i^T \pmb x_s) b=∣S∣1s∈S∑(ys−i∈S∑aiyixxxiTxxxs)
三、核函数
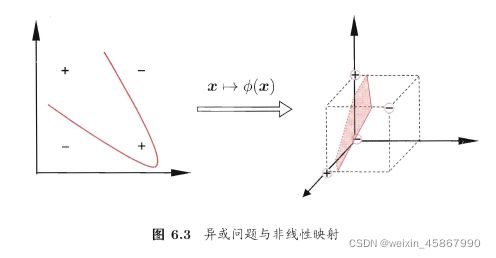
- 问题不一定是线性可分的,对这样的问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分,令 ϕ ( x ) \phi(\pmb x) ϕ(xxx)表示 x \pmb x xxx映射后的特征向量,在特征空间中划分超平面所对应的模型可表示为
f ( x ) = w T ϕ ( x ) + b f(\pmb x) = \pmb w^T \phi(\pmb x) + b f(xxx)=wwwTϕ(xxx)+b
并有
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 s . t . y i ( w T ϕ ( x ) + b ) ≥ 1 , i = 1 , 2 , ⋯ , m \underset {w,b}{\operatorname {min}}\frac{1}{2}||\pmb w||^2\\ s.t. \quad y_i(\pmb w^T \phi(\pmb x) + b)\geq 1,\quad i=1,2,\cdots,m w,bmin21∣∣www∣∣2s.t.yi(wwwTϕ(xxx)+b)≥1,i=1,2,⋯,m
其对偶问题是
max a ∑ i = 1 m a i − 1 2 ∑ i = 1 m ∑ j = 1 m a i a j y i y j ϕ ( x i ) T ϕ ( x j ) s . t . ∑ i = 1 m a i y i = 0 a i ≥ 0 , i = 1 , 2 , ⋯ , m \underset {\pmb a}{\operatorname {max}}\sum_{i=1}^ma_i - \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m a_i a_j y_i y_j\phi(\pmb x_i)^T\phi(\pmb x_j)\\ s.t.\quad \sum_{i=1}^m a_i y_i =0\\ a_i \geq0,\quad i=1,2,\cdots,m aaamaxi=1∑mai−21i=1∑mj=1∑maiajyiyjϕ(xxxi)Tϕ(xxxj)s.t.i=1∑maiyi=0ai≥0,i=1,2,⋯,m
κ ( x i , x j ) = < ϕ ( x i , x j ) > = ϕ ( x i ) T ϕ ( x j ) \kappa(\pmb x_i, \pmb x_j)=<\phi(\pmb x_i,\pmb x_j)>=\phi (\pmb x_i)^T \phi (\pmb x_j) κ(xxxi,xxxj)=<ϕ(xxxi,xxxj)>=ϕ(xxxi)Tϕ(xxxj)
替换式中相关项,求解得到
f ( x ) = w T ϕ ( x ) + b = ∑ i = 1 m a i y I ϕ ( x i ) T ϕ ( x j ) + b = ∑ i = 1 m a i y i κ ( x i , x j ) + b \begin{aligned} f(\pmb x) &= \pmb w^T\phi (\pmb x) +b\\ &=\sum_{i=1}^m a_i y_I \phi(\pmb x_i)^T\phi(\pmb x_j)+b\\ &=\sum_{i=1}^ma_i y_i\kappa(\pmb x_i, \pmb x_j) + b \end{aligned} f(xxx)=wwwTϕ(xxx)+b=i=1∑maiyIϕ(xxxi)Tϕ(xxxj)+b=i=1∑maiyiκ(xxxi,xxxj)+b
其中 κ ( ⋅ , ⋅ ) \kappa(\cdot,\cdot) κ(⋅,⋅)就是 “核函数”(kernel function),式中显示出模型最优解可通过训练样本的核函数展开,这一展开式亦称“支持向量展开式”(support vector expansion) - 定理:令 χ \chi χ为输入空间, κ ( ⋅ , ⋅ ) \kappa(\cdot,\cdot) κ(⋅,⋅)是定义在 χ × χ \chi \times \chi χ×χ上的对称函数,则 κ \kappa κ是核函数当且仅当对于任意 D = { x 1 , x 2 , ⋯ , x m } D=\{\pmb x_1, \pmb x_2,\cdots,\pmb x_m\} D={xxx1,xxx2,⋯,xxxm},“核矩阵”(kernel matrix) K \Kappa K是半正定的:
K = [ κ ( x 1 , x 1 ) ⋯ κ ( x i , x j ) ⋯ κ ( x 1 , x m ) ⋮ ⋱ ⋮ ⋱ ⋮ κ ( x i , x 1 ) ⋯ κ ( x i , x j ) ⋯ κ ( x i , x m ) ⋮ ⋱ ⋮ ⋱ ⋮ κ ( x m , x 1 ) ⋯ κ ( x m , x j ) ⋯ κ ( x m , x m ) ] \Kappa= \begin{bmatrix} \kappa(\pmb x_1, \pmb x_1)&\cdots&\kappa(\pmb x_i, \pmb x_j)&\cdots&\kappa(\pmb x_1, \pmb x_m)\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ \kappa(\pmb x_i, \pmb x_1)&\cdots&\kappa(\pmb x_i, \pmb x_j)&\cdots&\kappa(\pmb x_i, \pmb x_m)\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ \kappa(\pmb x_m, \pmb x_1)&\cdots&\kappa(\pmb x_m, \pmb x_j)&\cdots&\kappa(\pmb x_m, \pmb x_m)\\ \end{bmatrix} K=⎣⎢⎢⎢⎢⎢⎢⎡κ(xxx1,xxx1)⋮κ(xxxi,xxx1)⋮κ(xxxm,xxx1)⋯⋱⋯⋱⋯κ(xxxi,xxxj)⋮κ(xxxi,xxxj)⋮κ(xxxm,xxxj)⋯⋱⋯⋱⋯κ(xxx1,xxxm)⋮κ(xxxi,xxxm)⋮κ(xxxm,xxxm)⎦⎥⎥⎥⎥⎥⎥⎤ - 定理表明,只要一个堆成函数所对应的核矩阵半正定,它就能作为核函数使用。事实上,对于一个半正定核矩阵,总能找到一个与之对应的映射 ϕ \phi ϕ。换言之,任何一个核函数都隐式地定义了一个称为 “再生核希尔伯特空间”(Reproducing Kernel Hilbert Space,简称RKHS) 的特殊空间
- “核函数选择”成为支持向量机的最大变数

此外,还可通过函数组合得到,例如: - 若 κ 1 \kappa_1 κ1和 κ 2 \kappa_2 κ2为核函数,则对于任意正数 γ 1 \gamma_1 γ1和 γ 2 \gamma_2 γ2,其线性组合
γ 1 κ 1 + γ 2 κ 2 \gamma_1\kappa_1+\gamma_2\kappa_2 γ1κ1+γ2κ2
也是核函数
κ 1 ⊗ κ 2 ( x , z ) = κ 1 ( x , z ) κ 2 ( x , z ) \kappa_1 \otimes \kappa_2(\pmb x,\pmb z) =\kappa_1(\pmb x,\pmb z)\kappa_2(\pmb x,\pmb z) κ1⊗κ2(xxx,zzz)=κ1(xxx,zzz)κ2(xxx,zzz)
直积也是核函数
对于任意函数 g ( x ) g(x) g(x),
κ ( x , z ) = g ( x ) κ 1 ( x , z ) g ( z ) \kappa(\pmb x,\pmb z)= g(\pmb x)\kappa_1(\pmb x,\pmb z)g(\pmb z) κ(xxx,zzz)=g(xxx)κ1(xxx,zzz)g(zzz)
也是核函数
四、软间隔与正则化
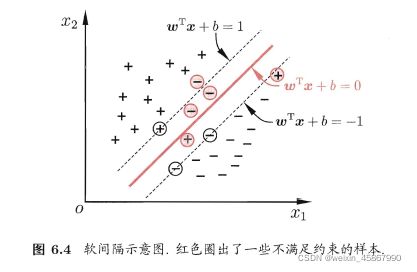
- 所有样本均满足约束,即所有样本都必须划分正确,成为“硬间隔”(hard margin),而“软间隔”(soft margin)允许某些样本不满足约束
y i ( w T x i + b ) ≥ 1 y_i(\pmb w^T \pmb x_i +b) \geq 1 yi(wwwTxxxi+b)≥1
当然,在最大化间隔的同时,不满足约束的样本应尽可能少,优化目标可写为
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ℓ 0 / 1 ( y i ( w T x i + b ) − 1 ) , \underset {w,b}{\operatorname {min}}\frac{1}{2}||\pmb w||^2 +C\sum_{i=1}^m \ell_{0/1}(y_i(\pmb w^T\pmb x_i +b )-1), w,bmin21∣∣www∣∣2+Ci=1∑mℓ0/1(yi(wwwTxxxi+b)−1),
其中 C > 0 C>0 C>0是一个常数, ℓ 0 / 1 \ell_{0/1} ℓ0/1是”0/1损失函数“
ℓ 0 / 1 ( z ) = { 1 , i f z < 0 ; 0 , o t h e r w i s e . \ell_{0/1}(z)= \begin{cases} 1, \quad if z<0;\\ 0, \quad otherwise. \end{cases} ℓ0/1(z)={1,ifz<0;0,otherwise. - 当C为无穷大时,迫使所有样本均满足约束;当C取有限值时,允许一些样本不满足约束
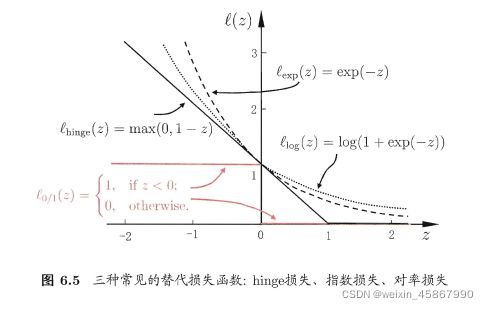
- 0/1 不连续,数学性质不好,“替代损失”(surrogate loss) 一般具有较好的数学性质,如它们通常是凸连续函数且是 ℓ 0 / 1 \ell_{0/1} ℓ0/1的上界,三种常用的替代损失函数:
h i n d g e 损 失 函 数 : ℓ h i n g e ( z ) = m a x ( 0 , 1 − z ) ; 指 数 损 失 ( e x p o n e n t i a l l o s s ) : ℓ e x p ( z ) = e x p ( − z ) 对 率 损 失 ( l o g i s t i c l o s s ) : ℓ l o g ( z ) = l o g ( 1 + e x p ( − z ) ) hindge损失函数:\ell_{hinge}(z)=max(0,1-z);\\ 指数损失(exponential loss):\ell_{exp}(z)=exp(-z)\\ 对率损失(logistic loss): \ell_{log}(z)=log(1+exp(-z)) hindge损失函数:ℓhinge(z)=max(0,1−z);指数损失(exponentialloss):ℓexp(z)=exp(−z)对率损失(logisticloss):ℓlog(z)=log(1+exp(−z))
若采用hinge损失,则变成:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m max ( 0 , 1 − y i ( w T x i + b ) ) \underset {w,b}{\operatorname {min}} \frac{1}{2}||\pmb w||^2+C\sum_{i=1}^m\operatorname {max}(0,1-y_i(\pmb w^T \pmb x_i +b)) w,bmin21∣∣www∣∣2+Ci=1∑mmax(0,1−yi(wwwTxxxi+b))
引用“松弛变量”(slack variables) ξ i ≥ 0 \xi_i\geq0 ξi≥0,可将式重写为
min w , b , ξ i 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ξ i s . t . y i ( w T x i + b ) ≥ 1 − ξ i ξ i ≥ 0 , i = 1 , 2 , ⋯ , m . \underset {w,b,\xi_i}{\operatorname {min}}\frac{1}{2}||\pmb w||^2+C\sum_{i=1}{m}\pmb \xi_i\\ s.t.\quad y_i(\pmb w^T \pmb x_i + b)\geq1-\xi_i\\ \xi_i \geq0, \quad i=1,2,\cdots,m. w,b,ξimin21∣∣www∣∣2+Ci=1∑mξξξis.t.yi(wwwTxxxi+b)≥1−ξiξi≥0,i=1,2,⋯,m.
这就是常用的“软间隔支持向量机”,仍是一个二次规划问题,类似的,通过拉格朗日乘子法得到
L ( w , b , α , ξ , μ ) = 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ξ i + ∑ i = 1 m α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 m μ i ξ i \begin{aligned} L(\pmb w,b ,\pmb \alpha, \pmb \xi, \pmb \mu)&=\frac{1}{2}||\pmb w||^2+C\sum_{i=1}^m\xi_i\\ &+\sum_{i=1}^m\alpha_i(1-\xi_i-y_i(\pmb w^T \pmb x_i + b))-\sum_{i=1}^m\mu_i\xi_i\\ \end{aligned} L(www,b,ααα,ξξξ,μμμ)=21∣∣www∣∣2+Ci=1∑mξi+i=1∑mαi(1−ξi−yi(wwwTxxxi+b))−i=1∑mμiξi
推导过程略
对软间隔支持向量机,KKT条件
{ α i ≥ 0 , μ i ≥ 0 , y i f ( x i ) − 1 + ξ i ≥ 0 , α i ( y i f ( x i ) − 1 + ξ i ) = 0 , ξ i ≥ 0 , μ i ξ i = 0. \begin{cases} \alpha_i\geq0,\quad \mu_i\geq0,\\ y_if(\pmb x_i)-1+\xi_i\geq 0,\\ \alpha_i(y_if(\pmb x_i)-1+\xi_i)=0,\\ \xi_i\geq0,\mu_i\xi_i=0. \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧αi≥0,μi≥0,yif(xxxi)−1+ξi≥0,αi(yif(xxxi)−1+ξi)=0,ξi≥0,μiξi=0.
- 软间隔支持向量最终模型仅与支持向量有关,即通过采用hinge损失函数仍保持了稀疏性
- 如果使用对率损失函数 ℓ l o g \ell_{log} ℓlog来替代式中的0/1损失函数,则几何得到了对率回归模型
- 对率回归的优势主要在于其输出具有自然的概率意义,即在给出预测标记的同时也给出了概率。而支持向量机的输出不具有概率意义,欲得到概率输出需进行特殊处理
- 对率回归能够直接用于多分类任务,支持向量机为此则需要进行推广
- 对数回归的解依赖于更多的训练样本,其预测开销更大
- 可写为一般形式
min f Ω ( f ) + C ∑ i = 1 m ℓ ( f ( x i ) , y i ) , \underset {f}{\operatorname {min}}\Omega(f)+C\sum_{i=1}^m\ell(f(\pmb x_i),y_i), fminΩ(f)+Ci=1∑mℓ(f(xxxi),yi),
其中 Ω ( f ) \Omega(f) Ω(f)称为 “结构风险”(structural risk),用于描述模型f的某些性质;第二项 ∑ i = 1 m ℓ ( f ( x i ) , y i ) \sum_{i=1}^m\ell(f(\pmb x_i),y_i) ∑i=1mℓ(f(xxxi),yi)称为 “经验风险”(empirical risk),用于描述模型与训练数据的契合度;C用于对二者进行折中。 - 从风险最小化的角度来看, Ω ( f ) \Omega(f) Ω(f)表达了我们希望获得具有何种性质的模型,这为引入领域知识和用户意图提供了途径;另一方面,该信息有助于削减假设空间,从而降低最小化训练误差的过拟合风险。从这个角度来说,上式称为 “正则化”(regularization) 问题, Ω ( f ) \Omega(f) Ω(f)称为正则化项,C则称为正则化常数, L P \operatorname L_P LP范数(norm)是常用的正则化项
- 其中L2范数 ∣ ∣ w ∣ ∣ 2 ||\pmb w||^2 ∣∣www∣∣2倾向于 w \pmb w www的分量取值尽量均衡,即非零分量个数尽量稠密,而L0范数 ∣ ∣ w ∣ ∣ 0 ||\pmb w||_0 ∣∣www∣∣0和L1范数 ∣ ∣ w ∣ ∣ 1 ||\pmb w||_1 ∣∣www∣∣1则倾向 w \pmb w www的分量尽量稀疏,即非零向量个数尽量少
五、支持向量回归
- 支持向量回归(Support Vector Regression,简称SVR)
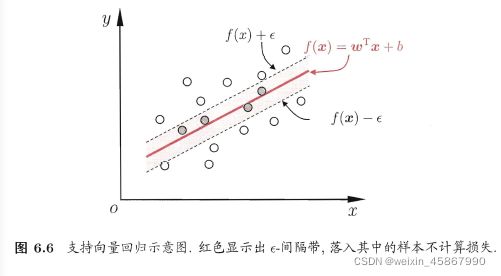 SVR 问题可形式化为
SVR 问题可形式化为
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ℓ ϵ ( f ( x i ) − y i , \underset {w,b}{\operatorname {min}}\frac{1}{2}||\pmb w||^2+C\sum_{i=1}^m\ell_{\epsilon}(f(\pmb x_i)-y_i, w,bmin21∣∣www∣∣2+Ci=1∑mℓϵ(f(xxxi)−yi,
其中C为正则化常数, ℓ ϵ \ell_{\epsilon} ℓϵ是图中所示的 ϵ \epsilon ϵ-不敏感损失( ϵ \epsilon ϵ-insensitive loss)函数
ℓ ϵ ( z ) = { 0 , if ∣ z ∣ ≤ ϵ ; ∣ z ∣ − ϵ , otherwise \ell_{\epsilon}(z)= \begin{cases} 0,\quad \operatorname {if}|z|\leq\epsilon;\\ |z|-\epsilon, \quad \operatorname{otherwise} \end{cases} ℓϵ(z)={0,if∣z∣≤ϵ;∣z∣−ϵ,otherwise
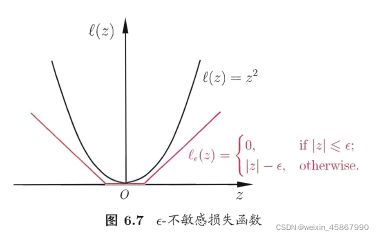
引入松弛变量 ξ i \xi_i ξi和 ξ ^ i \hat \xi_i ξ^i,可将式重写为
min w , b , ξ i , ξ ^ i 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ( ξ i + ξ ^ i ) s . t . f ( x i ) − y i ≤ ϵ + ξ i y i − f ( x i ) ≤ ϵ + ξ ^ i ξ i ≥ 0 , ξ ^ i ≥ 0 , i = 1 , 2 , ⋯ , m . \underset{w,b,\xi_i,\hat \xi_i}{\operatorname {min}}\frac{1}{2}||\pmb w||^2+C\sum_{i=1}^m(\xi_i+\hat \xi_i)\\ s.t. \quad f(\pmb x_i)-y_i \leq \epsilon + \xi_i\\ y_i- f(\pmb x_i)\leq \epsilon + \hat \xi_i\\ \xi_i\geq0,\hat \xi_i \geq 0,i=1,2,\cdots,m. w,b,ξi,ξ^imin21∣∣www∣∣2+Ci=1∑m(ξi+ξ^i)s.t.f(xxxi)−yi≤ϵ+ξiyi−f(xxxi)≤ϵ+ξ^iξi≥0,ξ^i≥0,i=1,2,⋯,m.
推导过程略
KKT条件
{ α i ( f ( x i ) − y i − ϵ − ξ i ) = 0 , α ^ i ( y i − f ( x i ) − ϵ − ξ ^ i ) = 0 , α i α ^ i = 0 , ξ i ξ ^ i = 0 ( C − α i ) ξ i = 0 , ( C − α ^ i ) ξ ^ i = 0. \begin{cases} \alpha_i(f(\pmb x_i)-y_i-\epsilon -\xi_i)=0,\\ \hat \alpha_i(y_i-f(\pmb x_i)-\epsilon -\hat \xi_i)=0,\\ \alpha_i\hat \alpha_i=0,\xi_i\hat \xi_i=0\\ (C-\alpha_i)\xi_i=0,(C-\hat \alpha_i)\hat \xi_i=0. \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧αi(f(xxxi)−yi−ϵ−ξi)=0,α^i(yi−f(xxxi)−ϵ−ξ^i)=0,αiα^i=0,ξiξ^i=0(C−αi)ξi=0,(C−α^i)ξ^i=0.
- 仅当样本 ( x i , y i ) (\pmb x_i,y_i) (xxxi,yi)不落入 ϵ \epsilon ϵ-间隔带中,相应的 α i \alpha_i αi和 α ^ i \hat \alpha_i α^i才能取非零值
SVR可表示为
f ( x ) = ∑ i = 1 m ( α ^ i − α i ) κ ( x , x i ) + b f(\pmb x)=\sum_{i=1}^m(\hat \alpha_i - \alpha_i)\kappa(\pmb x, \pmb x_i) +b f(xxx)=i=1∑m(α^i−αi)κ(xxx,xxxi)+b
其中 κ ( x i , x j ) = ϕ ( x i ) T ϕ ( x j ) \kappa(\pmb x_i, \pmb x_j)=\phi(\pmb x_i)^T\phi(\pmb x_j) κ(xxxi,xxxj)=ϕ(xxxi)Tϕ(xxxj)
这节推导部分很多,省略了很多
六、核方法
- “表示定理”(representer theorem)令 H \mathbb{H} H为核函数 κ \kappa κ对应的再生核希泊尔特空间, ∣ ∣ h ∣ ∣ H ||h||_{H} ∣∣h∣∣H表示空间中关于h的范数,对于任意单调递增函数 Ω : [ 0 , ∞ ) ↦ R \Omega:[0,\infty)\mapsto \mathbb{R} Ω:[0,∞)↦R和任意非损失函数 ℓ : R ↦ [ 0 , ∞ ] \ell:\mathbb{R}\mapsto[0,\infty] ℓ:R↦[0,∞],优化问题
min h ∈ H F ( h ) = Ω ( ∣ ∣ h ∣ ∣ H ) + ℓ ( h ( x 1 ) , h ( x 2 ) , ⋯ , h ( x m ) ) \underset{h\in \mathbb{H}}{\operatorname {min}}F(h) = \Omega(||h||_H)+\ell(h(\pmb x_1),h(\pmb x_2),\cdots,h(\pmb x_m)) h∈HminF(h)=Ω(∣∣h∣∣H)+ℓ(h(xxx1),h(xxx2),⋯,h(xxxm))
解总可以写为
h ∗ ( x ) = ∑ i = 1 m α i κ ( x , x i ) h^*(\pmb x) = \sum_{i=1}^{m}\alpha_i\kappa(\pmb x,\pmb x_i) h∗(xxx)=i=1∑mαiκ(xxx,xxxi) - 基于核函数的学习方法,统称为 “核方法”(kernel methods) 最常见的,是通过“核化”(即引入核函数)来将线性学习器拓展为非线性学习器
- “核线性判别分析”(Kernelized Linear Discriminant Analysis,简称KLDA)
先假设可通过某种映射 ϕ : χ ↦ F \phi:\chi\mapsto \mathbb{F} ϕ:χ↦F将样本映射到一个特征空间 F \mathbb{F} F,然后在 F \mathbb{F} F中执行线性判别分析,以求得
h ( x ) = w T ϕ ( x ) h(\pmb x)=\pmb w^T \phi(\pmb x) h(xxx)=wwwTϕ(xxx)
KLDA的学习目标是
max w J ( w ) = w T S b ϕ w w T S w ϕ w , \underset{w}{\operatorname {max}}J(\pmb w)=\frac{\pmb w^TS_b^{\phi}\pmb w}{\pmb w^TS_w^{\phi}\pmb w}, wmaxJ(www)=wwwTSwϕwwwwwwTSbϕwww,
S b ϕ S_b^{\phi} Sbϕ和 S w ϕ S_w^{\phi} Swϕ分别为训练样本在特征空间 F \mathbb{F} F中的类间散度矩阵和类内散度矩阵,令 X i X_i Xi表示第 i ∈ { 0 , 1 } i\in\{0,1\} i∈{0,1}类样本的集合,其样本数为 m i m_i mi;总样本数 m = m 0 + m 1 m=m_0+m_1 m=m0+m1.第i类样本在特征空间 F \mathbb{F} F中的均值为
μ i ϕ = 1 m i ∑ x ∈ X i ϕ ( x ) \pmb \mu_i^{\phi}=\frac{1}{m_i}\sum_{x \in X_i}\phi(\pmb x) μμμiϕ=mi1x∈Xi∑ϕ(xxx)
两个散度矩阵分别为
S b ϕ = ( μ 1 ϕ − μ 0 ϕ ) ( μ 1 ϕ − μ 0 ϕ ) T S w ϕ = ∑ i = 1 1 ∑ s ∈ X i ( ϕ ( x ) − μ i ϕ ) ( ϕ ( x ) − μ i ϕ ) T S_b^{\phi}=(\pmb \mu_1^{\phi}-\pmb \mu_0^{\phi})(\pmb \mu_1^{\phi}-\pmb \mu_0^{\phi})^T\\ S_w^{\phi}=\sum_{i=1}^1\sum_{s\in X_i}(\phi(\pmb x)-\pmb \mu_i^{\phi})(\phi(\pmb x)-\pmb \mu_i^{\phi})^T Sbϕ=(μμμ1ϕ−μμμ0ϕ)(μμμ1ϕ−μμμ0ϕ)TSwϕ=i=1∑1s∈Xi∑(ϕ(xxx)−μμμiϕ)(ϕ(xxx)−μμμiϕ)T
通常我们难以知道映射 ϕ 的 具 体 形 式 , 因 此 \phi的具体形式,因此 ϕ的具体形式,因此使用核函数 κ ( x , x i ) = ϕ ( x i ) T ϕ ( x ) \kappa(\pmb x,\pmb x_i)=\phi(\pmb x_i)^T\phi(\pmb x) κ(xxx,xxxi)=ϕ(xxxi)Tϕ(xxx)来隐式表达这个映射和特征空间 F \mathbb{F} F
由表示定理,函数 h ( x ) h(\pmb x) h(xxx)可写为
h ( x ) = ∑ i = 1 m α i κ ( x , x i ) = ∑ i = 1 m α i ϕ ( x i ) T ϕ ( x ) = ( ∑ i = 1 m α i ϕ ( x i ) ) T ϕ ( x ) \begin{aligned} h(\pmb x) &= \sum_{i=1}^m\alpha_i\kappa(\pmb x,\pmb x_i)\\ &=\sum_{i=1}^m\alpha_i\phi(\pmb x_i)^T\phi(\pmb x)\\ &=(\sum_{i=1}^m\alpha_i\phi(\pmb x_i))^T\phi(\pmb x) \end{aligned} h(xxx)=i=1∑mαiκ(xxx,xxxi)=i=1∑mαiϕ(xxxi)Tϕ(xxx)=(i=1∑mαiϕ(xxxi))Tϕ(xxx)
可得
w = ∑ i = 1 m α i ϕ ( x i ) \pmb w = \sum_{i=1}^m\alpha_i\phi(\pmb x_i) www=i=1∑mαiϕ(xxxi)
令 K ∈ R m × m \pmb K \in \mathbb R^{m\times m} KKK∈Rm×m为核函数 κ \kappa κ所对应的核矩阵, ( K ) i j = κ ( x i , x j ) (\pmb K)_{ij}=\kappa(\pmb x_i,\pmb x_j) (KKK)ij=κ(xxxi,xxxj).令 1 i ∈ { 1 , 0 } m × 1 1_i\in\{1,0\}^{m\times 1} 1i∈{1,0}m×1为第i类样本的指示向量,即 1 i 1_i 1i的第j个分量为1当且仅当 x j ∈ X i \pmb x_j\in X_i xxxj∈Xi,否则 1 i 1_i 1i的第j个分量为0.再令
μ ^ 0 = 1 m 0 K 1 0 , μ ^ 1 = 1 m 1 K 1 1 , M = ( μ ^ 0 − μ ^ 1 ) ( μ ^ 0 − μ ^ 1 ) T N = K K T − ∑ i = 0 1 m i μ ^ i μ ^ i T \hat \mu_0 = \frac{1}{m_0}\pmb K1_0,\\ \hat \mu_1 = \frac{1}{m_1}\pmb K1_1,\\ \pmb M = (\hat \mu_0 - \hat \mu_1)(\hat \mu_0 - \hat \mu_1)^T\\ \pmb N = \pmb K\pmb K^T - \sum_{i=0}^1m_i\hat \mu_i\hat \mu_i^T μ^0=m01KKK10,μ^1=m11KKK11,MMM=(μ^0−μ^1)(μ^0−μ^1)TNNN=KKKKKKT−i=0∑1miμ^iμ^iT
于是有
max α J ( α ) = α T M α α T N α \underset{\alpha}{\operatorname{max}}J(\pmb \alpha)= \frac{\pmb \alpha^T\pmb M \pmb \alpha}{\pmb \alpha^T\pmb N \pmb \alpha} αmaxJ(ααα)=αααTNNNααααααTMMMααα
显然,使用线性判别分析求解方法即可得到 α \pmb \alpha ααα,进而可得到投影函数 h ( x ) h(\pmb x) h(xxx)
总结
本节推导内容较多,省略了部分内容。