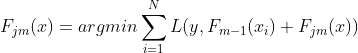（ 保证能看懂系列）集成算法之Boosting - GBDT回归算法 手推原理 以及 python 实现
Gradient boosting
Adaboost采用的是通过增加每个错分点的权重，减小对分点的权重，并且为每个弱分类器设置权重来获得最终的分类结果的。和Adaboost不同的是，Gradient boosting算法是通过不断拟合上一轮损失函数的负梯度来训练这一轮的学习器，其实就是将上一轮的损失函数的负梯度（在这里称为伪残差）作为训练数据的真实值，去拟合真实值。GBDT就是将弱分类器设为CART的Gradient boosting算法。
问题1. 如何理解“算法是通过不断拟合上一轮损失函数的负梯度来训练这一轮的学习器”
Gradient boosting算法依然采用加法模型,可以表示成如下形式： 
是learning rate
算法的目的是不断使得预测结果和真值之间的误差最小，也就是不断的减小损失函数的过程。即找到损失函数下降最快的方向，并按这个方向走。
问题2.损失函数最快的方向在哪里？
在参数空间内 
在
初的一次泰勒展开 
等式右边的向量点乘在两个向量共线的时候最大，
就是梯度方向，
表示的是参数的变化方向，所以下降最快的方向就是的负方向。以上的讨论是在参数空间的，在函数空间依然成立。总结：函数下降的最快的方向就是函数的负梯度方向
回答问题1，Gradient boosting算法是希望到损失函数下降最快的方向，那就是损失函数的负梯度方向
，并按照这个更新函数，所以我们的学习器
看这个学习器是不是就是损失函数的负梯度，那为什么说是拟合，而不是直接用负梯度作为学习器呢？我的理解是，在做这个算法得时候我们想让学习器变得越来越好，不仅仅局限于某个学习器，只要是损失函数可导都是可以的。所以这里面说用决策器去拟合。也就是在告诉我们，你是啥损失函数对我的算法的可用性是没有影响的。
Gradient boosting算法的通用流程：
input: dataset {
, 损失函数
，回归问题最常用的损失函数是平方损失函数
step 1 . 通过寻找损失函数最小是对应的
来设置初值
step 2. for m= 1 to M:
(a) 计算损失函数的负梯度值（也叫伪残差）
![r_{im}=\left [ -\frac{\partial }{\partial F(x)}L(y,F(x)) \right ] _{F(x)=F_{m-1}(x)}](http://img.e-com-net.com/image/info8/b3f050368a0c40c1be5857ab10010f07.gif)
(b) 建立学习器拟合以上残差，并建立每个叶子节点最终区域 
（就是记录在每个叶子节点的数据都有哪些,便于之后步骤的数据根据和伪残差修正）, j = 1,2...Jm ，Jm表示该树叶子节点的个数
（c）通过最小化每个节点中数据的损失函数和，计算每个节点的预测值 
(d)更新
,通过寻找某个数据x所对应的所有节点的预测值，一般情况下，某个数据只会在一个节点，但是对于有空值的数据来说，它会按照权重分别分配到不同的叶子结点中，可以参在CART的缺失值处理的博客，了解情况。如果不是缺失值的话，就直接找到对应的和相乘，再加上
即可。
step 3. 当达到最终学习器个数M或者伪残差小于要求时，即停止 ，输出
GBDT 回归算法
和Adaboost相比：
1 . Adaboost 起始于stump，
是根据第m个学习器补偿误差的能力决定的，与带权分类误差有关
2. GBDT算法一般开始于一个叶子,当预测一个连续值的时候，基于平方损失的GBDT的就是所有值的平均值。另外每个分类器不一定是stump，一般是8-32个叶子节点的树，但每一个树的size都应该是相同的。Adaboost scale每个分类器通过分类器的权重（有时候也能有乘上学习因子），权重可能不相同。GBDT 用的是相同的scale
3.Adaboost 分类器的损失函数是指数损失，GBDT算法的损失函数不受限制，一般情况分类用对数损失或者指数损失，回归用平方损失，绝对值损失，或者huber等
接下来根据Gradient boosting算法的通用流程，一步步看GBDT算法的思路：
input: dataset {, 损失函数
step 1 . 通过寻找损失函数最小是对应的来设置初值，可见此时初值就是所有数据的平均值
step 2. for m= 1 to M:
(a) 计算损失函数的负梯度值（也叫伪残差）,所以这里的结果就是伪残差就等于残差，这也是为什么这个损失函数前面有个1/2的系数的原因，但是仅仅只有在损失函数是平方损失的时候等于残差，其余都不等，所以叫伪残差
(b) 建立学习器拟合以上残差，并建立每个叶子节点最终区域 （就是记录在每个叶子节点的数据都有哪些,便于之后步骤的数据根据和伪残差修正）, j = 1,2...Jm ，Jm表示该树叶子节点的个数
（c）通过最小化每个节点中数据的损失函数和，计算每个节点的预测值 ，可见此时每个叶子节点的预测值就是该叶子节点所有残差的平均值
(d)更新,通过寻找某个数据x所对应的所有节点的预测值，一般情况下，某个数据只会在一个节点，但是对于有空值的数据来说，它会按照权重分别分配到不同的叶子结点中，可以参在CART的缺失值处理的博客，了解情况。如果不是缺失值的话，就直接找到对应的和相乘，再加上即可。
step 3. 当达到最终学习器个数M或者伪残差小于要求时，即停止 ，输出
这里用的CART回归树，可以参考这个博客来了解这部分内容https://blog.csdn.net/lanyuelvyun/article/details/88697386
以下是代码部分 弱学习器采用的是CART回归树
class DecisionTreeRegression():
def __init__(self,max_depth: int = None,min_samples_split:int = 5,
min_samples_leaf: int = 5,min_impurity_decrease: float =0.0):
'''
min_samples_split: 内部节点再划分所需最小样本数
min_samples_leaf: 叶子节点最少样本数 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝
分裂需要满足的最小增益
max_depth: 最大深度
min_impurity_decrease:分裂需要满足的最小增益
'''
self.max_depth = max_depth
self.min_samples_split = min_samples_split
self.min_samples_leaf = min_samples_leaf
self.min_impurity_decrease = min_impurity_decrease
self.nodes = 0
self.tree = None
self.type_feature = None
self.index = None
def __MSE(self,y):
'''
:param data:
:param y: 目标数据
:return: MSE: 返回该分支的MSE
'''
## 根据第一个公式
mean = np.mean(y)
mse = np.sum((y-mean)**2)
return mse
def __typeFeature(self,X):
# 表示特征是否为连续还是离散
n_sample,n_feature = X.shape
self.type_feature = []
#### 特征属性小于10个，认为是离散型数据用0表示，连续性数据用1 表示
for f_idx in range(n_feature):
if len(np.unique(X[:, f_idx]))< 10:
self.type_feature.append(0)
else:
self.type_feature.append(1)
return self.type_feature
def __binSplitData(self,X,y,index,f_idx,f_val):
### att 数有数据在第f_idx的特征的所有属性,将不等于 f_val 分为一类，其余分为另一类
#################### 0: 离散类型特征二分方法 1:连续数据 ############################
att=X[:, f_idx]
if self.type_feature[f_idx]== 0:
X_left = X[att == f_val]
X_right = X[att != f_val]
y_left = y[att == f_val]
y_right = y[att != f_val]
index_left = index[att == f_val]
index_right = index[att != f_val]
else:
X_left = X[att <= f_val]
X_right = X[att >f_val]
y_left = y[att <= f_val]
y_right = y[att > f_val]
index_left = index[att <= f_val]
index_right = index[att > f_val]
## 切分点和样本点的索引
return X_left, X_right, y_left, y_right,index_left,index_right
def __bestSplit(self,X,y,index):
'''
找到最佳分割特征与特征值
:param X
:return: best_f_idx 最佳分割特征 ， best_f_val 特征值
'''
best_mse = self.__MSE(y)
n_sample,n_feature = X.shape
best_f_idx = None
best_f_val = np.mean(y)
## 第一个终止条件： 当叶子节点中的样本数小于最小分割值，不再分割
if n_sample < self.min_samples_split:
return best_f_idx,best_f_val
##-------------------------通过不断二分的过程 寻找对于某个特征，的最佳分割点---------------------------
for f_idx in range(n_feature):
##-------------------------如果该特征中的属性个数小于10，则认为是离散数据 type_feature = 0，否则else---------------------------
if self.type_feature[f_idx] == 0:
for f_val in np.unique(X[:, f_idx]):
## 当某个特征只有两个类别时，仅仅做一次左右子树的划分，不用重复操作
if len(np.unique(X[:, f_idx]))== 2 and f_val == np.unique(X[:, f_idx])[0]:
continue
else:
X_left, X_right, y_left, y_right,index_left,index_right = self.__binSplitData(X,y,index,f_idx,f_val)
## 第二个终止条件： 分割后样本数据小于节点的最低样本数，则放弃分割
if len(index_left) best_mse:
continue
else:
## 更新最大增益和最佳分裂位置
best_mse = mse
best_f_idx,best_f_val = f_idx,f_val
##------------------------- 连续特征属性的二分 case = 1 ---------------------------
else:
for f_val in np.linspace(X[:, f_idx].min()+1,X[:, f_idx].max()-1,num=50):
X_left, X_right, y_left, y_right,index_left,index_right = self.__binSplitData(X,y,index,f_idx,f_val)
## 第二个终止条件： 分割后样本数据小于节点的最低样本数，则放弃分割
if len(index_left) best_mse:
continue
else:
## 更新最大增益和最佳分裂位置
best_mse = mse
best_f_idx,best_f_val = f_idx,f_val
return best_f_idx,best_f_val
def __CART(self,X,y,index):
'''
生成CART树
:param X： 特征数据
:param y: 目标数据
:return; CART 树
'''
best_f_idx, best_f_val = self.__bestSplit(X,y,index)
self.nodes += 1
# best_f_idx 为空表示不能接续划分，则该点为叶子结点 best_f_val
if best_f_idx is None:
return index
# 节点数超过最大深度的限制，也要返回叶节点，叶节点的值为当前数据中的目标值众数
if self.max_depth:
if self.nodes >= 2**self.max_depth:
return index
tree = dict()
tree['cut_f'] = best_f_idx
tree['cut_val'] = best_f_val
X_left, X_right, y_left, y_right,index_left,index_right = self.__binSplitData(X,y,index,best_f_idx,best_f_val)
tree['left_value'] = np.mean(y_left)
tree['right_value'] = np.mean(y_right)
tree['left'] = self.__CART(X_left,y_left,index_left)
tree['right'] = self.__CART(X_right,y_right,index_right)
return tree
def fit(self,X,y,sample_weight = None):
'''
拟合模型，数据应该是 ndarray or series类型，dataframe通过 df.values转变成ndarray，不会报错
:param X: 特征数据
:param: y: 目标数据
:param: sample_weight
:return: None
'''
if sample_weight is None:
## 使得每个数据的权值都是 1/len(X) *len(X)是产生 len(X)个
sample_weight = np.array([1/len(X)] * len(X))
# 标记每个特征是离散还是连续，从而采用不同的二分方法
self.index = np.array(range(len(X)))
self.type_feature = self.__typeFeature(X)
self.tree = self.__CART(X,y,self.index)
return self.tree
def predict(self,X_test):
'''
数据类别预测
:param X_test:预测数据
:return: y_: 类别预测结果
'''
return np.array([self.__predict_one(x_test, self.tree) for x_test in X_test])
def __predict_one(self,x_test,tree,label = None):
if isinstance(tree, dict): # 非叶节点才做左右判断
cut_f_idx, cut_val = tree['cut_f'], tree['cut_val']
if self.type_feature[cut_f_idx] == 0:
sub_tree = tree['left'] if x_test[cut_f_idx] == cut_val else tree['right']
label = tree['left_value'] if x_test[cut_f_idx] == cut_val else tree['right_value']
else:
sub_tree = tree['left'] if x_test[cut_f_idx] <= cut_val else tree['right']
label = tree['left_value'] if x_test[cut_f_idx] <= cut_val else tree['right_value']
return self.__predict_one(x_test, sub_tree,label)
else:
return label 然后是GBDT算法，按照以上步骤对照即可
class GBDTRegression():
def __init__(self,estimators: int = 10, classifier = DecisionTreeRegression,step: float = 0.1):
self.estimators = estimators
self.weakLearner = classifier
self.step = step
self.trees = []
self.F_init = None
def pseudoResiduals(self,y,predicted):
rm = y - predicted
return rm
def TerminalRegions(self,tree):
### 找到每一个叶子节点内的数据，或者说找到叶子节点包含的区域
global Rm
for key, val in tree.items():
if key == 'left' or key =='right':
if isinstance(tree[key],dict):
self.TerminalRegions(tree[key])
else:
Rm.append(val)
return Rm
def findRegions(self,x,Rm):
for i in rangr(len(Rm)):
(x == Rm[s[1]]).sum()
def fit(self,X,y):
self.F_init = np.mean(y)
## step1 通过寻找损失函数最小是对应的来设置初值
F_before = np.array([np.mean(y)] * len(X))
for m in range(self.estimators):
##(a) 计算损失函数的负梯度值（也叫伪残差）
rm = self.pseudoResiduals(y,F_before)
## (b) 建立学习器拟合以上残差，
tree_clf = self.weakLearner(max_depth = 4)
tree = tree_clf.fit(X, rm)
self.trees.append(tree_clf)
## 并建立每个叶子节点最终区域
global Rm
Rm = []
Rm = self.TerminalRegions(tree)
Jm = len(Rm)
gamma_m = np.zeros(len(X))
## （c）通过最小化每个节点中数据的损失函数和
for j in range(Jm):
gamma_m[Rm[j]] += np.mean(rm[Rm[j]])
## (d)更新
Fm = F_before + self.step * gamma_m
F_before = Fm
def predict(self,x_test):
M = self.estimators
y_ = np.array([self.F_init] * len(x_test))
for m in range(M):
a= self.trees[m].predict(X_test)
# print('a.shape -----------------------------',a.shape,y_.shape)
y_ += self.step * self.trees[m].predict(X_test)
return y_ 测试数据 波士顿房价
if __name__ == '__main__':
from sklearn import datasets
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
house_dataset = datasets.load_boston(); #加载波士顿房价数据集
scaler = StandardScaler()
X = scaler.fit_transform(house_dataset.data)
Y = house_dataset.target
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)
tree_clf = GBDTRegression(estimators = 100)
tree_clf.fit(X_train, Y_train)
Y_pred = tree_clf.predict(X_test)
print('acc:{}'.format(np.sum((Y_pred - Y_test)**2) / len(Y_test)))
del tree_clf
from sklearn.ensemble import GradientBoostingRegressor
tree_clf = GradientBoostingRegressor()
tree_clf.fit(X_train, Y_train)
Y_pred = tree_clf.predict(X_test)
print('sklearn acc:{}'.format(np.sum((Y_pred - Y_test)**2) / len(Y_test)))