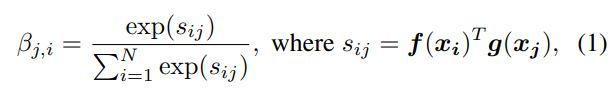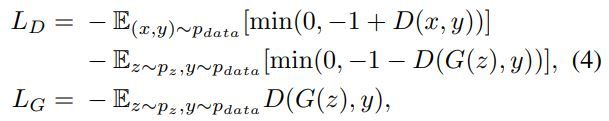Self-Attention Generative Adversarial Networks
Self-Attention Generative Adversarial Networks
在本文中，我们提出了自注意生成对抗网络（SAGAN），它允许对图像生成任务进行注意驱动的远程依赖建模。传统的卷积GANs只在低分辨率特征图中产生局部空间点的函数，从而产生高分辨率的细节。此外，鉴别器可以检查图像的遥远部分中的高度详细的特征是否彼此一致。此外，最近的工作表明，generator conditioning GAN的性能。利用这一观点，我们将光谱标准化应用于GAN生成器，并发现这改善了训练表现。在具有挑战性的ImageNet数据集上，提出的SAGAN比以前的工作表现得更好，将发布的最佳初始分数从36.8提高到52.52，并将Frechet初始距离从27.62降低到18.65。注意层的可视化显示，生成器利用与对象形状相对应的邻域，而不是固定形状的局部区域。
1. Introduction
图像合成是计算机视觉中的一个重要问题。随着生成对抗网络（GANs）的出现，这个方向已经有了显著的进展（Goodfellow等人，2014），尽管仍有许多开放的问题（Odena，2019）。基于深度卷积网络的GANs（Radford等人，2016；Karras等人，2018；Zhang等人）特别成功。然而，通过仔细检查这些模型生成的样本，我们可以观察到卷积GANs（Odena等人，2017；Miyato等人，2018；Miyato & Koyama，2018）在多类数据集（如ImageNet（Russakovsky等人，2015））上训练时，对某些图像类别建模的难度远远大于其他。
例如，虽然最先进的ImageNet GAN模型（Miyato & Koyama，2018）擅长合成结构限制较少的图像类别（例如海洋、天空和景观类别，它们更多的是通过纹理而不是几何来区分），但它未能捕捉到一些类别中持续出现的几何或结构模式（例如，狗经常被画上逼真的毛皮纹理，但没有明确定义的独立脚）。一个可能的解释是，以前的模型严重依赖卷积来模拟不同图像区域之间的依赖关系。由于卷积算子有一个局部的感受野，长距离的依赖关系只有在通过几个卷积层之后才能被处理。
由于各种原因，这可能会妨碍对长期依赖关系的学习：一个小模型可能无法表示它们，优化算法可能难以发现仔细协调多个层以捕获这些依赖关系的参数值，而且这些参数化在统计上可能是脆弱的，当应用到以前未见过的输入时容易失败。增加卷积核的大小可以增加网络的表示能力，但这样做也会损失使用局部卷积结构获得的计算和统计效率。Self-attention（Cheng等人，2016；Parikh等人，2016年；另一方面，Vaswani等人（2017年）在建模长期相关性的能力与计算和统计效率之间表现出更好的平衡。Self-attention模块将某个位置的响应计算为所有位置特征的加权和，其中权重（或注意向量）的计算只需要很小的计算成本。
在这项工作中，我们提出了Self-attention生成对抗网络（SAGANs），它将Self-attention机制引入卷积GANs。Self-attention模块是对卷积的补充，有助于对跨图像区域的长距离、多层次的依赖关系进行建模。有了Self-attention，生成器可以绘制图像，其中每个位置的精细细节都与图像的远处部分的精细细节仔细协调。此外，判别器还能更准确地执行全局图像上的复杂几何约束。结构。
除了Self-attention，我们还纳入了最近关于网络调节与GAN性能的见解。Odena等人（2018）的工作表明，well-conditioned生成器往往表现更好。我们建议使用spectral normalization技术强制执行GAN生成器的良好条件，该技术之前只应用于判别器（Miyato等人，2018）。
我们在ImageNet数据集上进行了广泛的实验，以验证所提出的Self-attention机制和稳定技术的有效性。SAGAN在图像合成方面的表现明显优于先前的工作，它将报告的最佳is从36.8提高到52.52，并将Frechet入射距离´从27.62降低到18.65。注意力层的可视化显示，生成器利用了对应于物体形状的邻域，而不是固定形状的局部区域。Our code is available at https://github.com/ brain-research/self-attention-gan.
3. Self-Attention Generative Adversarial Networks
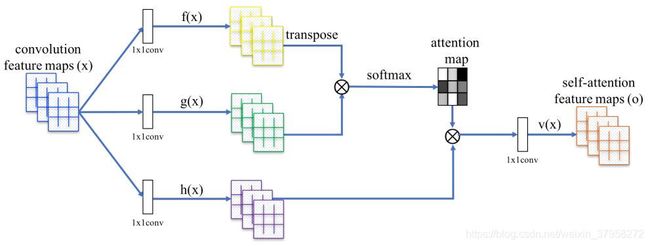
图2. 为SAGAN提出的自我关注模块。⊗表示矩阵乘法。对每一行进行softmax操作。
大多数基于GAN的图像生成模型（Radford等人，2016；Salimans等人，2016；Karras等人，2018）是使用卷积层构建的。卷积处理局部邻域的信息，因此单独使用卷积层对图像中的长距离依赖关系进行建模在计算上是低效的。在本节中，我们调整了（Wang等人，2018）的非局部模型，将自我关注引入到GAN框架中，使生成器和判别器都能有效地模拟相隔甚远的空间区域之间的关系。我们把所提出的方法称为自我注意生成对抗网络（SAGAN），因为它有自我注意模块（见图2）。
首先将前一隐藏层的图像特征 x ∈ R C × N x∈\mathbb R^{C×N} x∈RC×N转化为两个特征空间f，g来计算注意力，其中 f ( x ) = W f x ， g ( x ) = W g x f(x)=W_fx，g(x)=W_gx f(x)=Wfx，g(x)=Wgx
β j , i β_{j,i} βj,i表示模型在合成第j个区域时对第i个位置的关注程度。这里，C是通道的数量，N是前一个隐藏层的特征位置的数量。注意层的输出为$o = (o_1, o_2, …, o_j , …, o_N ) ∈ \mathbb R^{C×N} $，其中
在上述公式中， W g ∈ R C ‾ × C ， W f ∈ R C ‾ × C ， W h ∈ R C ‾ × C ， W v ∈ R C ‾ × C W_g∈\mathbb R^{\overline C×C}，W_f∈\mathbb R^{\overline C×C}，W_h∈\mathbb R^{\overline C×C}，W_v∈\mathbb R^{\overline C×C} Wg∈RC×C，Wf∈RC×C，Wh∈RC×C，Wv∈RC×C是权重矩阵，它们被实现为1×1卷积。因为在减少C的通道数时，我们没有注意到任何显著的性能下降¯ 为C/k，其中k=1，2，4，8，在ImageNet上经过几个训练周期。对于内存效率，我们选择k=8（即C¯ =C/8) 在我们所有的实验中。
此外，我们进一步将注意力层的输出乘以一个比例参数，并将输入的特征图加回。因此，最终的输出是由
其中γ是一个可学习的标量，初始化为0。引入可学习的γ允许网络首先依赖本地邻域的线索–因为这比较容易–然后逐渐学习给non-local evidence分配更多的权重。我们这样做的直观原因很简单：我们想先学习简单的任务，然后逐步增加任务的复杂性。在SAGAN中，建议的注意力模块已经应用于生成器和鉴别器，它们通过最小化对抗性损失的hinge版本以交替的方式进行训练（Lim & Ye，2017；Tran等人，2017；Miyato等人，2018）。
4. Techniques to Stabilize the Training of GANs
我们还研究了两种技术来稳定GANs在挑战性数据集上的训练。首先，我们在生成器以及判别器中使用 spectral normalization（Miyato等人，2018）。其次，我们证实了twotimescale update rule（TTUR）（Heusel等人，2017）是有效的，我们主张专门用它来解决正则化判别器的缓慢学习。
4.1. Spectral normalization for both generator and discriminator
Miyato等人（Miyato et al., 2018）最初提出通过对判别器网络应用谱归一化来稳定GAN的训练。这样做是通过限制每一层的频谱规范来约束判别器的Lipschitz常数。与其他归一化技术相比，频谱归一化不需要额外的超参数调整（将所有权重层的频谱规范设置为1在实践中一直表现良好）。此外，其计算成本也相对较小。
我们认为，根据最近的证据，the generator is an important causal factor in GANs’ performance（Odena等人，2018），生成器也可以从光谱正常化中受益。生成器中的频谱正常化可以防止参数大小的升级，避免不寻常的梯度。我们通过经验发现，生成器和鉴别器的频谱归一化使得每次生成器更新可以使用更少的鉴别器更新，从而大大降低了训练的计算成本。该方法还显示出更稳定的训练行为。
4.2. Imbalanced learning rate for generator and discriminator updates
在以前的工作中，判别器的正则化（Miyato等人，2018；Gulrajani等人，2017）往往会减慢GANs的学习过程。在实践中，使用正则化判别器的方法通常需要在训练期间的每个生成器更新步骤中进行多个（例如5个）判别器更新。Heusel等人（Heusel等人，2017）独立地主张对生成器和判别器使用单独的学习率（TTUR）。我们建议专门使用TTUR来补偿正则化判别器的缓慢学习问题，使得每一个生成器步骤可以使用更少的判别器步骤。使用这种方法，我们能够在相同的wall-clock time内产生更好的结果。
器步骤可以使用更少的判别器步骤。使用这种方法，我们能够在相同的wall-clock time内产生更好的结果。
Network structures and implementation details. 我们训练的所有SAGAN模型都是为了生成128×128的图像。默认情况下，光谱归一化（Miyato等人，2018）被用于生成器和判别器中的各层。与（Miyato & Koyama, 2018）类似，SAGAN在生成器中使用条件批量归一化，在判别器中使用投影。对于所有模型，我们使用adam优化器（Kingma & Ba, 2015），β1 = 0，β2 = 0.9进行训练。默认情况下，判别器的学习率为0.0004，生成器的学习率为0.0001。