HLS FIR低通滤波器的实现
低通滤波器的实现:
1:滤波器的基本原理:简单的来说就是我们输入一个信号,里面有些我们不想要的频率,所以我们设置一个滤波器来滤除掉我们不想要的频率成分,然后再输出。数学表达式:y(n) = x(n) *h(n) [符号表示卷积] 。其频域则是Y(Z) = X(Z) x h(z) 。但是我们想要实现其卷积,我们不会用其频域的表达式,频域的表达式只是方便我们计算,但是实现还是要用其时域的卷积。我们将时域的表达式打开就是下面的公式。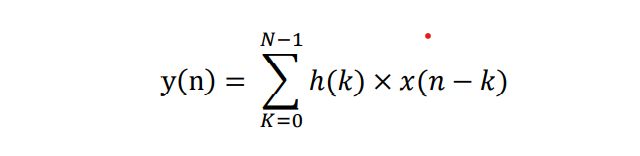
其中 x(n)为输入信号, h(n)为 FIR 滤波系数, y(n)为经过滤波后的输出信号,N为滤波器的抽头系数,N-1表示滤波器阶数。滤波器在FPGA中实现原理如下图,我们可以看出,其主要是由累加法器与乘法器构成。其思路就是将输入依次延迟一拍与其相应的滤波器系数相乘,然后将输出。
2:首先低通滤波器的参数我们用软件实现的,我们只需要进行一系列的设置就行了,然后将数据保存。我们滤波器的软件是''Filter Solutions 2011'',该软件的使用特别简单,我们只需要将滤波的参数进行设置,然后将滤波器的抽头系数进行保存,就行了。
3:将其数据导入matlab ,然后保存下来(这样做只是为了方便放入我们的hls的数组中)
4:进入hls进行滤波器的程序设计。在这里我就只是简单记录下其思路,然后具体代码我会贴在后面。滤波器就是一个系统,就是输入一个函数,经过滤波后输出一个函数,所以我们的函数的参数就只有一个输入,一个输出。该函数的思路就是为了为了实现乘法与累加。我们设计的是一个64阶的滤波器,所以会有64个相应的系数,前面的''Filter Solutions 2011''软件保存的系数就是其滤波器的系数。下面是代码,这里的是算法代码,并没有进行约束优化
这是.c代码
#include"fir_fliter.h"
void fir(data_in_t x,data_o_t *y){
const coef_t c[N] ={ 2, 2, 3, 3, 4, 5, 6, 8, 9, 11, 13, 16, 19, 21, 24, 27, 31, 34, 37, 41, 44, 47, 50, 53, 56, 58, 60, 62, 64, 65, 66, 66, 66, 66, 65, 64, 62, 60, 58, 56, 53, 50, 47, 44, 41, 37, 34, 31, 27, 24, 21, 19, 16, 13, 11, 9, 8, 6, 5, 4, 3, 3, 2, 2 };
//只是存储在内存中,用const 关键字修饰
static data_o_t shift[N]; //只会被初始化一次
acc_t acc = 0;;
int i ;
//移位寄存器
for(i = N-1; i >= 0;i--){
if(i == 0){
shift[0] = x;
acc += x*c[0];
}else {
shift[i] = shift[i-1];
acc += shift[i] *c[i];
}
}
*y = acc;
}
这是其对应的头文件,.h代码
#ifndef FIR_FLITER_H_
#define FIR_FLITER_H_
#define N 64
#define PI 3.1415926
#define AM 100
#define BIT_ACCURATE
#ifdef BIT_ACCURATE
#include"ap_int.h"
typedef ap_int<32> coef_t;
typedef ap_int<16> data_in_t;
typedef ap_int<32> data_o_t;
typedef ap_int<32> acc_t;
#else
typedef int coef_t;
typedef int data_in_t;
typedef int data_o_t;
typedef int acc_t;
#endif //end bit_accuate
#endif // end fir_fliter
void fir(data_in_t x,data_o_t *y);
5:接下来我们用再写一个testbench,进行仿真测试,其实只需要给与对应的激励就可以了,这里我们就直接产生两个正弦信号,然后进行合成,再输入到我们的滤波器函数,最后进行联合仿真,查看波形,看输出的波形是否完整。下面是testbench的程序
#include"fir_fliter.h"
#include
#include
int main(){
data_in_t signal_1;//12.8M
data_in_t signal_2;//0.78125m
data_in_t signal_3;//
data_o_t output;
const int SAMPLES = 1024; //采样点数
double value = (2*PI/8);
double value1 = (2*PI/128);
int i;
FILE *fp;
fp = fopen("output.data","w+");
//for循环会映射成时钟周期,相当于8个时钟周期采完一个正弦波
for(i = 0;i < SAMPLES;i++){
signal_1 =(data_in_t) AM * sin(value *(i % 8));//sin(2*pi*f*t);//12.5m
signal_2 =(data_in_t) AM * sin(value1 *(i % 128));//sin(2*pi*f*t);//0.78125
signal_3 = (signal_1 + signal_2)/2;
fir(signal_3,&output);
//S fprintf(stdout,"output[%d] = %d \r\n",i,( int )output);
fprintf(fp,"%d",( int )output);
}
fclose(fp);
return 0;
}
程序中我们产生正弦波可以直接用c语言中math.h。正弦信号形式y= sin(2*pi*f*t),采样即y(n)= sin(2*pi*f*t/fs),我这里第一个是用的8点,相当于一个周期内采8个点,而我们的时钟周期用的是100M。所以相当于输出的正弦波频率位100M/8 = 12.5M,而我们用C语言表示就是用模8,8点就可以得出一个完整的正弦波。程序中我们产生1个12.5M,0.78125M两个频率的正弦波,然后相加。可以看出我们的程序中都乘以了一个AM,AM = 100;因为标准正弦波的幅度的-1~1,我们乘以一个系数,进行放大,并进行强制类型转换。
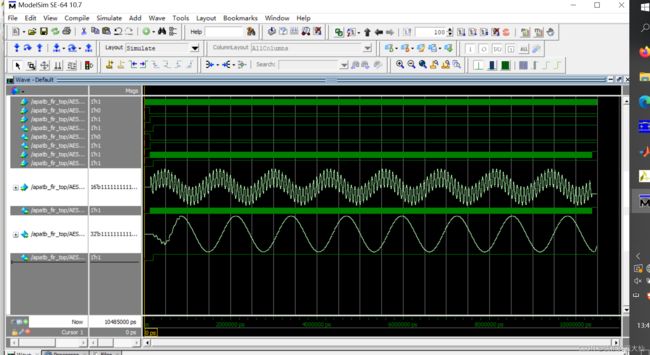
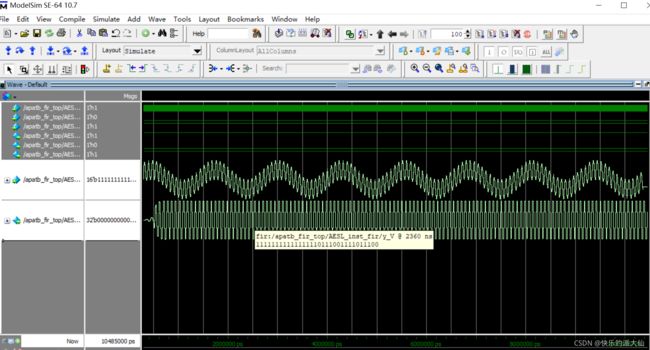
6:最后进行联合仿真,进入modesim查看波形,波形如下:
可以看出滤波效果还是很好的(留下的信号就是原混频信号的包络),剩下了低频型号。高频信号别滤除了。
7:在此基础上又进行高通,带通的测试结果如下
高通
带通:与低通了很相似,效果不是很好。
总结:本次还是学习到了很多的知识,学习到了几种波形的产生,并且进行了相应的滤波,还是比较有成就感,如果上述有问题,欢迎大家指出,如果大家需要这些的程序,或者需要''Filter Solutions 2011''这些都可以进行留言。