【数学】双根号求值域问题
∣ 双根号求值域问题 Nightguard Series. ∣ \begin{vmatrix}\Huge{\textsf{ 双根号求值域问题 }}\\\texttt{ Nightguard Series. }\end{vmatrix} ∣∣∣∣∣ 双根号求值域问题 Nightguard Series. ∣∣∣∣∣
求 f ( x ) = 3 x − 6 + 3 − x f(x)=\sqrt{3x-6}+\sqrt{3-x} f(x)=3x−6+3−x 的值域。
tips:请时刻小心定义域
♣ 1. 求导 \clubsuit 1.\texttt{求导} ♣1.求导
f ′ ( x ) = − 3 2 3 x − 6 + 1 2 3 − x = − 1 2 3 3 − x − 3 x − 6 ( 3 x − 6 ) ( 3 − x ) f'(x)=-\frac{3}{2\sqrt{3x-6}}+\frac{1}{2\sqrt{3-x}}=-\frac{1}{2}{\frac{3\sqrt{3-x}-\sqrt{3x-6}}{\sqrt{(3x-6)(3-x)}}} f′(x)=−23x−63+23−x1=−21(3x−6)(3−x)33−x−3x−6
令 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0 , 则 3 3 − x 0 − 3 x 0 − 6 = 0 ⇒ x 0 = 11 4 3\sqrt{3-x_0}-\sqrt{3x_0-6}=0 \Rightarrow x_0=\frac{11}{4} 33−x0−3x0−6=0⇒x0=411
f ( x ) f(x) f(x) 在 [ 2 , x 0 ) [2,x_0) [2,x0) 上单增,在 ( x 0 , 3 ] (x_0,3] (x0,3] 上单减
代入得 f ( x ) m a x = f ( x 0 ) = 2 , f ( x ) m i n = f ( 2 ) = 1. f(x)_{max}=f(x_0)=2,f(x)_{min}=f(2)=1. f(x)max=f(x0)=2,f(x)min=f(2)=1.
♣ 2. 三角换元 \clubsuit 2.\texttt{三角换元} ♣2.三角换元
f ( x ) = 3 x − 6 + 3 − x = 3 x − 2 + 3 − x f(x)=\sqrt{3x-6}+\sqrt{3-x}=\sqrt{3}\sqrt{x-2}+\sqrt{3-x} f(x)=3x−6+3−x=3x−2+3−x
令 a = x − 2 , b = 3 − x , a=\sqrt{x-2},b=\sqrt{3-x}, a=x−2,b=3−x, 则 a 2 + b 2 = 1 a^2+b^2=1 a2+b2=1 (三角换元的标志)
令 a = sin θ , b = cos θ a=\sin \theta, b=\cos \theta a=sinθ,b=cosθ
则 f ( x ) = 3 a + b = 3 sin θ + cos θ = 2 sin ( θ + π 6 ) f(x)=\sqrt{3}a+b=\sqrt{3}\sin\theta + \cos \theta =2\sin(\theta+\frac{\pi}{6}) f(x)=3a+b=3sinθ+cosθ=2sin(θ+6π)
∵ a , b > 0 \because a,b>0 ∵a,b>0 ,不妨令 θ ∈ [ 0 , π 2 ] \theta\in[0,\frac{\pi}{2}] θ∈[0,2π]
则 θ = π 3 \theta=\frac{\pi}{3} θ=3π 时取到最大值,
a = 3 2 , b = 1 2 ⇒ f ( x ) m a x = 2 , x = 11 4 ; a=\frac{\sqrt{3}}{2},b=\frac{1}{2} \Rightarrow f(x)_{max}=2,x=\frac{11}{4}; a=23,b=21⇒f(x)max=2,x=411;
θ = 0 \theta=0 θ=0 时取到最小值,
a = 0 , b = 1 ⇒ f ( x ) m i n = 1 , x = 2. a=0,b=1 \Rightarrow f(x)_{min}=1,x=2. a=0,b=1⇒f(x)min=1,x=2.
♣ 3. 向量法 \clubsuit 3.\texttt{向量法} ♣3.向量法
f ( x ) = 3 x − 6 + 3 − x = 3 x − 2 + 3 − x f(x)=\sqrt{3x-6}+\sqrt{3-x}=\sqrt{3}\sqrt{x-2}+\sqrt{3-x} f(x)=3x−6+3−x=3x−2+3−x
令 a ⃗ = ( 3 , 1 ) , b ⃗ = ( x − 2 , 3 − x ) \vec{a}=(\sqrt{3},1),\vec{b}=(\sqrt{x-2},\sqrt{3-x}) a=(3,1),b=(x−2,3−x) ,则 a ⃗ ⋅ b ⃗ = f ( x ) \vec{a}\cdot \vec{b}=f(x) a⋅b=f(x)
∵ ( x − 2 ) 2 + ( 3 − x ) 2 = 1 \because (\sqrt{x-2})^2+(\sqrt{3-x})^2=1 ∵(x−2)2+(3−x)2=1 为定值
∴ b ⃗ \therefore \vec{b} ∴b 终点的轨迹是一段圆弧。
如图:
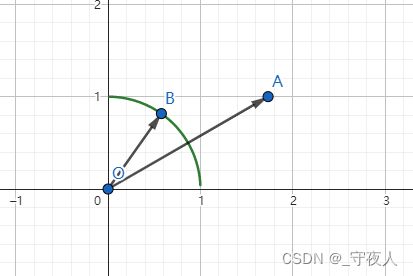
当 a ⃗ , b ⃗ \vec{a},\vec{b} a,b 共线时, a ⃗ ⋅ b ⃗ \vec{a}\cdot\vec{b} a⋅b 最大,为 ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ = 2 |\vec{a}|\cdot |{\vec{b}}|=2 ∣a∣⋅∣b∣=2 ,即 f ( x ) m a x = 2 , f(x)_{max}=2, f(x)max=2,
共线时 B B B 在直线 O A OA OA 上, ∴ 3 x − 2 = 3 − x ⇒ x = 11 4 ; \therefore \sqrt{3}\sqrt{x-2}=\sqrt{3-x} \Rightarrow x=\frac{11}{4}; ∴3x−2=3−x⇒x=411;
当 b ⃗ = ( 0 , 1 ) \vec{b}=(0,1) b=(0,1) 时, a ⃗ ⋅ b ⃗ \vec{a}\cdot\vec{b} a⋅b 最小,为 ∣ a ⃗ ∣ ∣ b ⃗ ∣ ⋅ π 3 = 1 |\vec{a}||{\vec{b}}|\cdot{\frac{\pi}{3}}=1 ∣a∣∣b∣⋅3π=1 ,即 f ( x ) m i n = 1 f(x)_{min}=1 f(x)min=1 ,此时 x = 2. x=2. x=2.
♣ 4. 线性规划 \clubsuit 4.\texttt{线性规划} ♣4.线性规划
令 a = 3 x − 6 , b = 3 − x , a=\sqrt{3x-6},b=\sqrt{3-x}, a=3x−6,b=3−x,
则 a 2 + 3 b 2 = 3 ⇒ a 2 3 + b 2 = 1 ( a , b > 0 ) a^2+3b^2=3 \Rightarrow \frac{a^2}{3}+b^2=1 (a,b>0) a2+3b2=3⇒3a2+b2=1(a,b>0)
f ( x ) = a + b ⇒ b = − a + f ( x ) f(x)=a+b \Rightarrow b=-a+f(x) f(x)=a+b⇒b=−a+f(x)
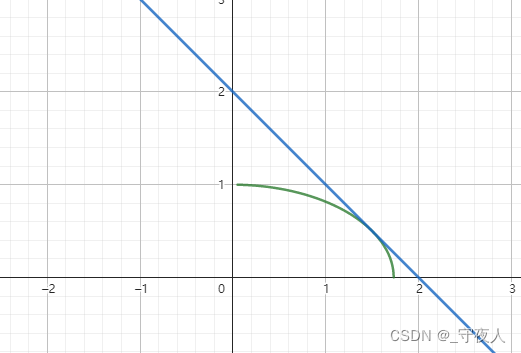
如图,即求椭圆在第一象限的部分 C : x 2 3 + y 2 = 1 ( x , y > 0 ) C:\frac{x^2}{3}+y^2=1 (x,y>0) C:3x2+y2=1(x,y>0) 与 l : y = − x + m l:y=-x+m l:y=−x+m 有交点时 m m m 的范围。
当 l l l 与 C C C 相切时 m m m 最大,
C C C 的切线方程: x 0 x 3 + y 0 y = 1 \frac{x_0x}{3}+y_0y=1 3x0x+y0y=1
∵ k = − 1 ∴ x 0 3 = y 0 , \because k=-1 \therefore \frac{x_0}{3}=y_0, ∵k=−1∴3x0=y0, 与 C C C 方程联立得切点: P ( 3 2 , 1 2 ) P(\frac{3}{2},\frac{1}{2}) P(23,21)
∴ l : y = − x + 2 = 0 , m m a x = 2 , \therefore l:y=-x+2=0,m_{max}=2, ∴l:y=−x+2=0,mmax=2, 即 f ( x ) m a x = 2 , f(x)_{max}=2, f(x)max=2,
a = 3 2 , b = 1 2 ⇒ x = 11 4 . a=\frac{3}{2},b=\frac{1}{2}\Rightarrow x=\frac{11}{4}. a=23,b=21⇒x=411.
当 l l l 与 C C C 交点为 ( 1 , 0 ) (1,0) (1,0) 时 m m m 最小,即 f ( x ) m i n = 1 , f(x)_{min}=1, f(x)min=1,
a = 0 , b = 1 ⇒ x = 2. a=0,b=1 \Rightarrow x=2. a=0,b=1⇒x=2.
或者,令 a = x − 2 , b = 3 − x , a=\sqrt{x-2},b=\sqrt{3-x}, a=x−2,b=3−x,
则 a 2 + b 2 = 1 , f ( x ) = 3 a + b ⇒ b = − 3 a + f ( x ) a^2+b^2=1,f(x)=\sqrt{3}a+b \Rightarrow b=-\sqrt{3}a+f(x) a2+b2=1,f(x)=3a+b⇒b=−3a+f(x)
像这样化成圆再做的话也可以。(其实相当于仿射变换)
♣ 5. 柯西不等式 \clubsuit 5.\texttt{柯西不等式} ♣5.柯西不等式
3 x − 6 + 3 − x = 3 x − 2 + 1 ⋅ 3 − x ≤ ( 3 + 1 ) ( 3 − x + x − 2 ) = 2. \sqrt{3x-6}+\sqrt{3-x}=\sqrt{3}\sqrt{x-2}+1\cdot \sqrt{3-x} \leq\sqrt{(3+1)(3-x+x-2)}=2. 3x−6+3−x=3x−2+1⋅3−x≤(3+1)(3−x+x−2)=2.
当且仅当 3 1 = x − 2 3 − x \frac{\sqrt{3}}{1}=\frac{{\sqrt{x-2}}}{{\sqrt{3-x}}} 13=3−xx−2 时取到最大值,解得 x = 11 4 x=\frac{11}{4} x=411
在知道函数单调性的前提下,代入端点求最小值
♣ 6. n元均值不等式 \clubsuit 6.\texttt{n元均值不等式} ♣6.n元均值不等式
3 x − 6 + 3 − x \sqrt{3x-6}+\sqrt{3-x} 3x−6+3−x
= 3 3 x − 2 + 3 3 x − 2 + 3 3 x − 2 + 3 − x =\frac{\sqrt{3}}{3}\sqrt{x-2}+\frac{\sqrt{3}}{3}\sqrt{x-2}+\frac{\sqrt{3}}{3}\sqrt{x-2}+\sqrt{3-x} =33x−2+33x−2+33x−2+3−x
由 Σ a n n ≤ Σ a n 2 n \frac{\Sigma a_n}{n} \leq \sqrt{\frac{\Sigma a_n^2}{n}} nΣan≤nΣan2 得
原式 ≤ 4 [ ( 3 3 x − 2 ) 2 + ( 3 3 x − 2 ) 2 + ( 3 3 x − 2 ) 2 + ( 3 − x ) 2 ] ) = 2 \leq\sqrt{4[{(\frac{\sqrt{3}}{3}\sqrt{x-2})^2+(\frac{\sqrt{3}}{3}\sqrt{x-2})^2+(\frac{\sqrt{3}}{3}\sqrt{x-2})^2+(\sqrt{3-x})^2]})}=2 ≤4[(33x−2)2+(33x−2)2+(33x−2)2+(3−x)2])=2
当且仅当 3 3 x − 2 = 3 − x \frac{\sqrt{3}}{3}\sqrt{x-2}=\sqrt{3-x} 33x−2=3−x ,即 x = 11 4 x=\frac{11}{4} x=411 时取到最大值
在知道函数单调性的前提下,代入端点求最小值
♣ 7. 通解 \clubsuit 7.\texttt{通解} ♣7.通解
https://www.bilibili.com/video/BV1mU4y1Y7Wh
8.开挂
只是想展示函数的图像而已 有个直观印象