《智能计算系统》课程报告——《An Efficient FPGA Accelerator Optimized for High Throughput Sparse CNN Inference》学习笔记
介绍
Wen, J., Ma, Y., & Wang, Z. (2020). An Efficient FPGA Accelerator Optimized for High Throughput Sparse CNN Inference. 2020 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), 165-168.
摘要
剪枝技术能够对CNN模型进行压缩，通过不重要权重置零来降低大型CNN模型的计算量。然而，对于硬件架构来说，通过高并行来载入和操作非0数据是一项巨大的挑战，这是由于减枝权重的位置是随机的。为解决这个问题，本文提出了一项稀疏感知的CNN加速器，来处理不规则减枝的CNN模型。本文设计了一种候选池架构来挑选出由非零权重选择所需的随机激活操作。这里使用了一种三维结构来缓解随机非零权值和高并发带来的负载不均衡。此外，还设计了专门的索引方法来配合池架构来完成整个稀疏数据流。提出的稀疏感知CNN加速器在Intel-Arria-10-FPGA上，与基线设计相比，在多个常见的CNN模型上实现了高达89.7%的吞吐率提升。
1 引言
CNN精度的巨大提升在很大程度上依赖于大量计算复杂性的增加，使得计算平台的复旦严重增加，带来了较高能耗和较长延时。为了降低CNN处理的计算消耗和内存负担，许多研究表明减枝技术【1_Han_2015_LearningBW, 2_Han_2016_Deep, 3_Yang_2017_Designing】是十分有效的。减枝对CNN模型进行剪裁，移除了不重要的参数，并对模型进行微调使其精度回复到损失可以忽略不计的程度。由于低于某个阈值的权重会被设为0，因此减枝会给CNN模型引入大量的稀疏性，而卷积和全连接层中对0值的MAC操作是多余的，因此这些稀疏性给跳过冗余的MAC操作提供了机会。
近些年来，FPGA成为了一种流行的加速CNN的硬件平台，这是因为FPGA具有可编程、大规模并行以及计算节能的特质。因此，许多基于FPGA进行CNN推理的加速器【4_Zhang_2015_Optimizing_FA, 5_Guo_2018_Angel_Eye, 6_Guan_2017_FPDNN】在设计上具有计算密集能源高效的特点。然而，大多数这类FPGA加速器的设计是面向于密集网络处理常规的卷积操作，因此无法从剪枝减少的权重和操作中获得收益。CNN中减枝的权重位置是不具有规律性，这给硬件加速器上对非0数据进行高并发的数据存取和计算带来了挑战。尽管之前有工作致力于高效利用剪枝CNN的稀疏性【8_Zhang_2016_CambriconX, 9_Lu_2018_SpWA, 10_Parashar_2017_SCNN】，这些方法仍然面临，对非0权值复杂的索引解码、用于转换所需输入在数据总线上巨大的硬件开销、以及由于负载不均衡引起的正比于模型压缩率的理论性能提升无法实现。
为了解决上述问题，本文提出一种稀疏感知基于FPGA的推理加速器，最大化地利用由CNN剪枝带来的计算量和数据缩减。本文还提出了一种可选的池数据流架构预取相应非0权重所需的输入激活值。非0权重的随机性和高并发会带来负载不均衡，所提出的池架构可以有效的减轻该问题。一种简单的索引模块被用来对非0权重的坐标进行解码，并控制整个推理过程的顺序执行。所提出的方法论和推理加速器对随机稀疏的CNN模型效果显著，在Intel-Arria-10-FPGA上对于VGG和ResNet的性能提升分别为89.7%和70.82%，相较于基线密集运算加速器。
文章之后的内容将按照如下结构展开。第2章将对数据流和架构进行详细说明。第3章展示评测和实验结果。结论部分将在第4章给出。
2. 稀疏感知卷积核
A. 整体架构
图1展示了提出稀疏卷积加速器的整体架构。
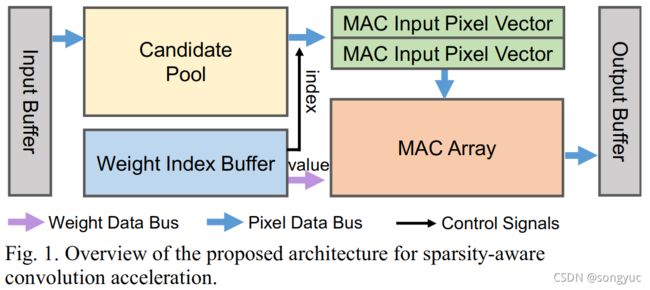所提出稀疏加速器的关键部件是用于从输入缓冲中预取相应激活值，例如：候选池模块。一种权重索引缓冲被配置为存储紧凑权重。只有非0权重的值会被一其相应索引连续地存储在这个缓冲区中。在进行稀疏卷积处理时，加速器会依据权重索引从候选池中选取激活值，其中权重索引是从权重缓冲区中解码得来的。之后，选取的MAC输入像素向量将会被送入MAX阵列并且与同时解码得到的权重值进行运算。
本文中稀疏感知的数据流是【7_Ma_2018_OptimizingC】工作的扩展，此工作使用了循环展开策略来重用权重和激活值的片上数据来最小化片段求和的存储和访问。卷积层由四层循环组成，在权重核和特征图上滑动。在一层中输入和输出特征图通道到由 N i f Nif Nif和 N o f Nof Nof来标记。权重核是一个四维张量，其大小为 N i f × N k x × N k y × N o f Nif\times Nkx \times Nky \times Nof Nif×Nkx×Nky×Nof，其中一个卷积核的大小为 N k x × N k y Nkx \times Nky Nkx×Nky。为了获得一个最终的输出激活值， N i f Nif Nif卷积核中的 N k x × N k y Nkx \times Nky Nkx×Nky个权重将和 N i f Nif Nif输入通道中的相应激活值进行乘加运算（MAC）。在本文中，卷积MAC运算由 N k x × N k y Nkx \times Nky Nkx×Nky核window顺序执行，并在整个 N i f Nif Nif通道输入特征图上依次进行，以获得最终的输出激活值。并行计算是沿着特征图的宽度和高度、并在多个输出通道上，特征图宽高分别由 P o x Pox Pox和 P o y Poy Poy来表示，输出通道数由 P o f Pof Pof来表示。
B. 候选池
候选池模块被设计成从输入缓冲区中预取所需的像素，并在MAC单元中使用。基于【7_Ma_2018_OptimizingC】中卷积并行计算的模式，完成并行计算一次迭代的输入像素的范围，需要通过输入特征图中的展开系数来计算，例如： P o x Pox Pox和 P o y Poy Poy，以及网络的配置，例如：步长和卷积核，如图2(a)所示。
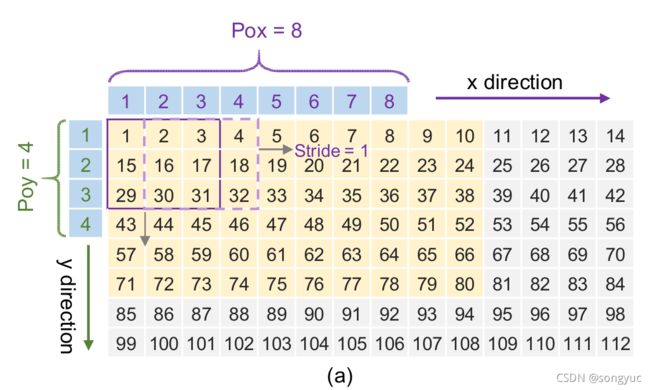
则候选像素范围能够由 P o x × S t r i d e + N k x − S t r i d e Pox\times Stride+Nkx-Stride Pox×Stride+Nkx−Stride以及 P o y × S t r i d e + N k y − S t r i d e Poy\times Stride+Nky-Stride Poy×Stride+Nky−Stride来表示，黄色区域中候选矩阵的宽和高则分别是 8 × 1 + 3 − 1 = 10 8\times1+3-1=10 8×1+3−1=10和 4 × 1 + 3 − 1 = 6 4\times1+3-1=6 4×1+3−1=6。
非0权重的随机分布会引起的负载不均衡的问题，并且横跨多个输出通道上的并行计算也会影响加速器的实际性能。图3(a)展示了在输入通道维度中的负载不均衡，
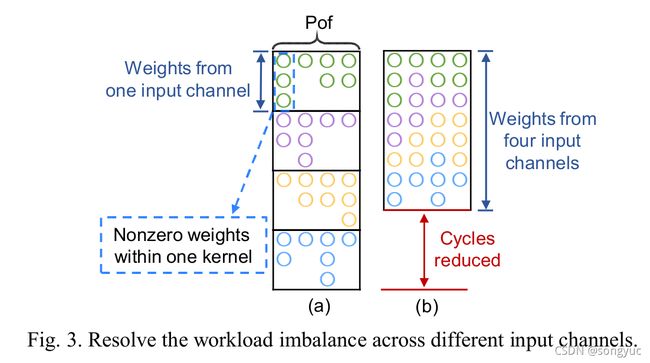
为了解决这个问题，作者将候选池设置成一种三维结构，此结构能够将将多达四个通道的像素聚集在一起。通过这种方式，作者能串行连续地在四个相邻输入通道上进行卷积操作，如图3(b)所示，而不需要等到最重负载的最差路径，于是可以极大地降低处理循环。章节3-A通过评测此设计在不同并行程度下的结果，展示了这种三维架构的有效性。
C. MAC输入像素向量
在像素被载入到候选池中之后，它们需要被输入到MAC单元阵列中与随机分布的非0权值进行卷积。为了实现这个操作，非0权值会与索引一同存储以记录它们的位置信息（编码方法将会在2-D中介绍）。这些预取的像素被称作MAC输入像素向量，其范围取决于非0权重的位置。
如图4所示，一个核中有三种非0权重的位置分布， 1 D _ l o c \mathit{1D\_loc} 1D_loc、 2 D _ l o c \mathit{2D\_loc} 2D_loc和 3 D _ l o c \mathit{3D\_loc} 3D_loc。
章节2-D将会详细介绍获得这三种位置的方法，即解码权重索引。本章节将关注于如何使用这些位置来正确地从候选阵列中预取像素。
1）权重的2D位置索引。图2(b)展示了一个非0权重位置索引如何决定，MAC输入像素像素在候选阵列中的范围。当某个非0权重沿着先 x x x方向后 y y y方向滑动时，该权重在像素候选阵列中的相应范围则会相应确定下来。之后，这些所选的MAC输入像素向量会被送入MAC阵列，并与相应非0权重一起进行计算来获得输出结果，其过程如图2(c)所示。
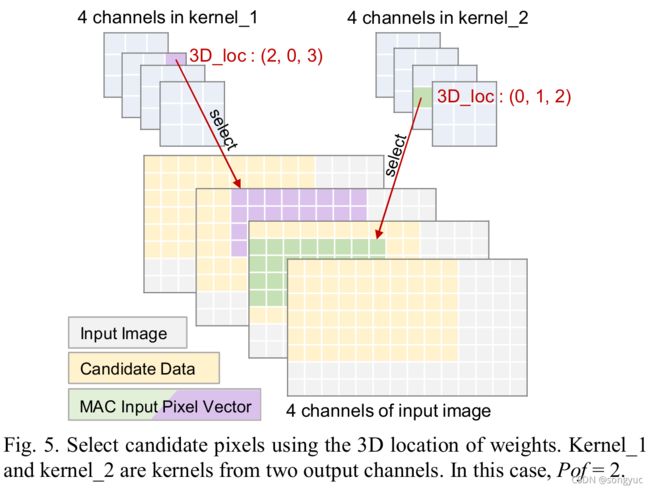
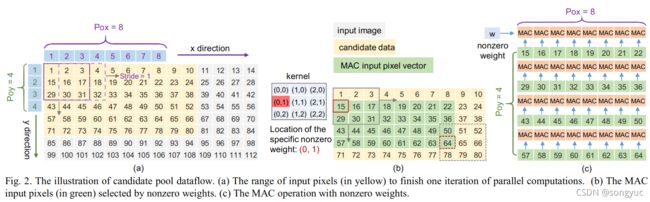2）权重的3D位置索引。 2 D _ l o c ( x , y ) \mathit{2D\_loc}\left(x,y\right) 2D_loc(x,y)是用来限制，在一个输入通道的候选阵列内，MAC输入像素向量的范围。 3 D _ l o c ( x , y , c h ) \mathit{3D\_loc}\left(x,y,ch\right) 3D_loc(x,y,ch)将“所选范围”从一个输入通道扩展到多个输入通道。举例来说，图5展示了两个来自两个输出通道的位置为 ( 2 , 0 , 3 ) \left(2,0,3\right) (2,0,3)和 ( 0 , 1 , 2 ) \left(0,1,2\right) (0,1,2)的非0权重，从唯一相同候选阵列的四个输入通道中选取其相应像素的过程。
3）Stride=2的情况。当stride=2时，数据流与stride=1时类似，在前面进行了叙述。由章节2-B中提到的候选大小表达式可知，stride=2时的候选序列比stride=1时序列要“更大”，从而适应这两种情况。此外，MAC 输入像素向量是在候选阵列中以一个像素间隔选择的。
D. 权重存储
此章节将会讲述针对非0权重硬件友好的编码方法以及相应的存储模式。
1）权重位置编码。主要思想是使用 i f m a p _ d i f f \mathit{ifmap\_diff} ifmap_diff和 l o c _ d i f f \mathit{loc\_diff} loc_diff来记录非0权重在不同循环维度中的相对位置。 i f m a p _ d i f f \mathit{ifmap\_diff} ifmap_diff表示两个输入通道中两个给定非0权重的索引之差。举例来说，如果 i f m a p _ d i f f = 1 \mathit{ifmap\_diff}=1 ifmap_diff=1，则说明此非0权重三古下一个输入通道的第一个非0权重，如图6所示；而当 i f m a p _ d i f f = 0 \mathit{ifmap\_diff}=0 ifmap_diff=0则表明非0权重仍位于同一个通道中。
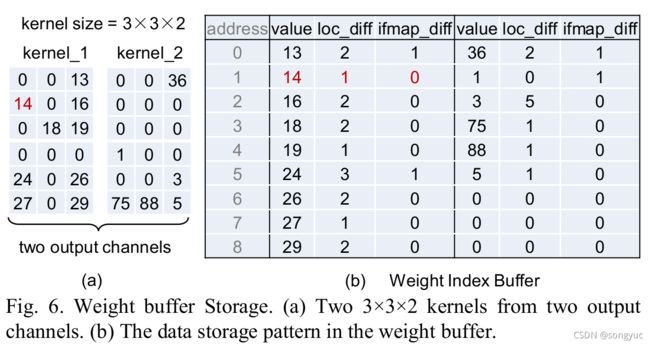
备注：这里的input-channel(输入通道)表示输入张量的一层，也就是 1 × H × W 1\times H \times W 1×H×W。
l o c _ d i f f \mathit{loc\_diff} loc_diff记录了一个输入通道内非0权重的相对位置。通过累加 l o c _ d i f f \mathit{loc\_diff} loc_diff的值，可以获得这些非0权重的1D位置。
备注：这里有点类似于步骤索引的方法，使用步长字符串表示非0权重间的距离。
这里， P o f \mathit{Pof} Pof个非0权重被存储在同一个地址中，从而实现 P o f \mathit{Pof} Pof输出通道的并行计算。如同图5中的示例所示，来自两个输出通道的非0权重可以并行地进行计算。
