人工智能导论-神经网络篇——反向传输计算及代码实现
手算前向与后向神经网络
其中,
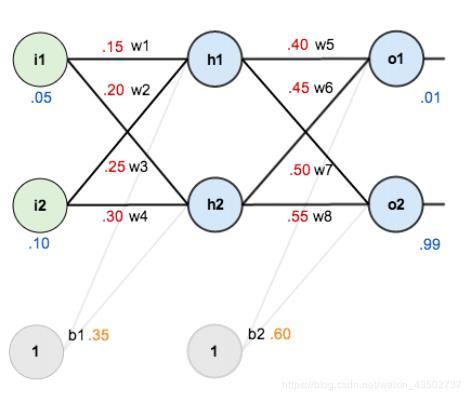
输入数据 i1=0.05,i2=0.10;
输出数据 o1=0.01,o2=0.99;
初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;
w5=0.40,w6=0.45,w7=0.50,w8=0.55
激活函数 sigmoid函数
1 1 + e − x \frac{1}{1+e^{-x}} 1+e−x1
损失函数(与老师上课板书内容一致,课件中均方差不同)
1 2 ( y − o u t ) 2 \frac{1}{2}(y-out)^2 21(y−out)2
目标:给出输入数据i1,i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
给出解答
前向传播:
输入->隐藏层:
n e t h 1 = i 1 × w 1 + i 2 × w 2 + 1 × b 1 = 0.15 ∗ 0.05 + 0.2 ∗ 0.1 + 0.35 ∗ 1 = 0.3775 net_{h1}=i1\times w1+i2\times w2+1\times b1=0.15*0.05+0.2*0.1+0.35*1=0.3775 neth1=i1×w1+i2×w2+1×b1=0.15∗0.05+0.2∗0.1+0.35∗1=0.3775
o u t h 1 = s i g m i o d ( n e t h 1 ) = 0.5933 out_{h1}=sigmiod\left( net_{h1} \right) =0.5933 outh1=sigmiod(neth1)=0.5933
同理
o u t h 2 = s i g m i o d ( n e t h 2 ) = 0.5969 out_{h2}=sigmiod\left( net_{h2} \right) =0.5969 outh2=sigmiod(neth2)=0.5969
隐藏层->输出层
同样算法可以得到:
n e t o 1 = w 5 × o u t h 1 + w 6 × o u t h 2 + b 2 × 1 net_{o1}=w5\times out_{h1}+w6\times out_{h2}+b2\times 1 neto1=w5×outh1+w6×outh2+b2×1
o u t o 1 = s i g m o i d ( n e t o 1 ) = 0.7514 out_{o1}=sigmoid\left( net_{o1} \right) =0.7514 outo1=sigmoid(neto1)=0.7514
o u t o 2 = s i g m o i d ( n e t o 2 ) = 0.7729 out_{o2}=sigmoid\left( net_{o2} \right) =0.7729 outo2=sigmoid(neto2)=0.7729
我们得到输出值为[0.7514,0.7729],与实际值[0.01 , 0.99]相差还很远,
所以我们需要对权值进行修改,然后使得实际值与输出值相似。此时我们需要对其进行反向传播。
反向传播:
本质上,我们是使用梯度下降法,求出我们误差函数与各权值的偏导数,我门根据偏导数去修正权值。其具体过程如下
更新的权值:
w i ( t + 1 ) = w i ( t ) − η ∂ E t o t a l ∂ w i w_i^{\left( t+1 \right)}=w_i^{\left( t \right)}-\eta \frac{\partial E_{total}}{\partial w_i} wi(t+1)=wi(t)−η∂wi∂Etotal
损失函数:
E t o t a l = ∑ 1 2 ( o u t t a r g e t − o u t o ) 2 E_{total}=\sum{\frac{1}{2}\left( out_{target}-out_o \right) ^2} Etotal=∑21(outtarget−outo)2
以修正 w 5 w_5 w5为例:
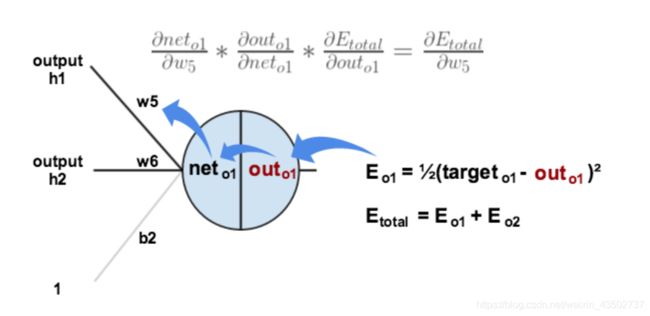
w 5 ( 1 ) = w 5 ( 0 ) − η ∂ E t o t a l ∂ w i w_5^{\left( 1 \right)}=w_5^{\left( 0 \right)}-\eta \frac{\partial E_{total}}{\partial w_i} w5(1)=w5(0)−η∂wi∂Etotal
∂ E t o t a l ∂ w 5 = ∂ E t o t a l ∂ o u t o 1 ∗ ∂ o u t o 1 ∂ n e t o 1 ∗ ∂ n e t o 1 ∂ w 5 \frac{\partial E_{total}}{\partial w_5}=\frac{\partial E_{total}}{\partial out_{o1}}*\frac{\partial out_{o1}}{\partial net_{o1}}*\frac{\partial net_{o1}}{\partial w_5} ∂w5∂Etotal=∂outo1∂Etotal∗∂neto1∂outo1∗∂w5∂neto1
E t o t a l = 1 2 ( y t a r g e t − o 1 − o u t o 1 ) 2 + 1 2 ( y t a r g e t − o 2 − o u t o 2 ) 2 E_{total}=\frac{1}{2}\left( y_{target-o1}-out_{o1} \right) ^2+\frac{1}{2}\left( y_{target-o2}-out_{o2} \right) ^2 Etotal=21(ytarget−o1−outo1)2+21(ytarget−o2−outo2)2
∂ E t o t a l ∂ o u t o 1 = 1 2 ∗ 2 ( y t a r g e t − o 1 − o u t o 1 ) 2 − 1 ∗ ( − 1 ) = o u t o 1 − y t a r g e t − o 1 \frac{\partial E_{total}}{\partial out_{o1}}=\frac{1}{2}*2\left( y_{target-o1}-out_{o1} \right) ^{2-1}*\left( -1 \right) =out_{o1}-y_{target-o1} ∂outo1∂Etotal=21∗2(ytarget−o1−outo1)2−1∗(−1)=outo1−ytarget−o1
∂ o u t o 1 ∂ n e t 01 = d sigmoid ( o u t o 1 ) d o u t o 1 = o u t o 1 ( 1 − o u t o 1 ) \frac{\partial out_{o1}}{\partial net_{01}}=\frac{d\ \text{sigmoid}\left( out_{o1} \right)}{d\ out_{o1}}=out_{o1}\left( 1-out_{o1} \right) ∂net01∂outo1=d outo1d sigmoid(outo1)=outo1(1−outo1)
∂ n e t o 1 ∂ w 5 = ∂ ( w 5 ∗ o u t h 1 + w 6 ∗ o u t h 2 + b 2 ∗ 1 ) ∂ w 5 = o u t h 1 \frac{\partial net_{o1}}{\partial w_5}=\frac{\partial \left( w_5*out_{h1}+w_6*out_{h2}+b_2*1 \right)}{\partial w_5}=out_{h1} ∂w5∂neto1=∂w5∂(w5∗outh1+w6∗outh2+b2∗1)=outh1
将上式代入数值,我们可以得出
∂ E t o t a l ∂ w 5 = 0.0822 \frac{\partial E_{total}}{\partial w_5}=0.0822 ∂w5∂Etotal=0.0822
从而,当学习率 η = 0.5 \eta=0.5 η=0.5
w 5 ( 1 ) = w 5 − η ∂ E t o t a l ∂ w 5 = 0.3589 w_5^{\left( 1 \right)}=w_5-\eta \frac{\partial E_{total}}{\partial w_5}=0.3589 w5(1)=w5−η∂w5∂Etotal=0.3589
同理我们可得w5,w6,w7,w8,
值得注意对于从隐藏层到输入层的反向传播:
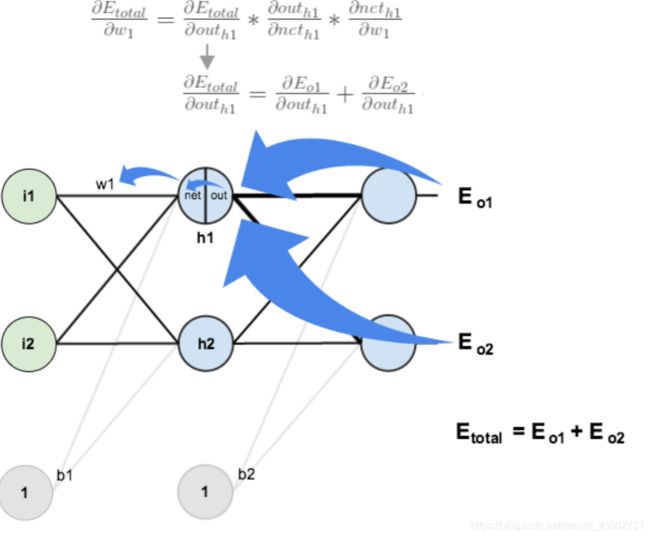
∂ E t o t a l ∂ w 1 = ∂ E t o t a l ∂ o u t h 1 ∗ ∂ o u t h 1 ∂ n e t h 1 ∗ ∂ n e t h 1 ∂ w 1 \frac{\partial E_{total}}{\partial w1}=\frac{\partial E_{total}}{\partial out_{h1}}*\frac{\partial out_{h1}}{\partial net_{h1}}*\frac{\partial net_{h1}}{\partial w1} ∂w1∂Etotal=∂outh1∂Etotal∗∂neth1∂outh1∗∂w1∂neth1
∂ E t o t a l ∂ o u t h 1 = ∂ E o 1 ∂ o u t h 1 + ∂ E o 2 ∂ o u t h 1 \frac{\partial E_{total}}{\partial out_{h1}}=\frac{\partial E_{o1}}{\partial out_{h1}}+\frac{\partial E_{o2}}{\partial out_{h1}} ∂outh1∂Etotal=∂outh1∂Eo1+∂outh1∂Eo2
∂ E o 1 ∂ o u t h 1 = ∂ E o 1 ∂ o u t o 1 ∗ ∂ o u t o 1 ∂ n e t o 1 \frac{\partial E_{o1}}{\partial out_{h1}}=\frac{\partial E_{o1}}{\partial out_{o1}}*\frac{\partial out_{o1}}{\partial net_{o1}} ∂outh1∂Eo1=∂outo1∂Eo1∗∂neto1∂outo1
基于 numpy 构建简单的三层回归神经网络。
实验目的:
1、了解反向传播网络的基本原理;
2、了解梯度下降法进行神经网络中的权值更新;
3、学习使用 numpy 编写简单的三层回归网络进行回归实验。
实验内容:
使用 numpy 库构建简单的数据集,编写简单的三层回归神经网络,输入和输出只有一个神经元,中间隐藏层可设置 N 个神经元,采用 sigmoid 函数作为激活函数。数据集按 y=x+随机噪声进行构建,x 取值为 0, 1, …, 19。学习梯度计算,及梯度下降法进行神经网络的权
值修改。
实验环境: python,numpy
实验步骤:
(1)确保 python 环境已经搭建完成。
(2)编写代码
本实验的神经网络图如下
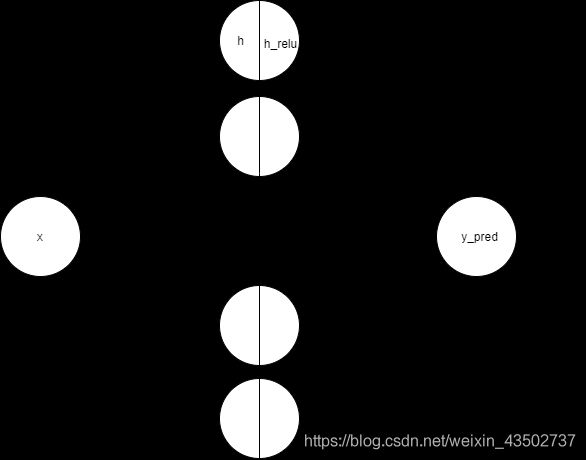
注意,这里的输出层不再需要激活函数。
代码如下:
import numpy as np
import matplotlib.pyplot as plt
def sigmoid_derivative(s):
ds = s * (1 - s)
return ds
def sigmoid(x):
s = 1 / (1 + np.exp(-x))
return s
# N:batch_size;
#D_in:输入维度
# H:隐藏层的维度;
#D_out:输出维度
N, D_in, H, D_out = 20, 1, 64, 1
# 随机生成一批数据
np.random.seed(0)
x = np.arange(0,N,1).reshape(N,D_in)*1.0 #20*1
y = x + np.random.randn(N,D_out) #20*1
# 随机初始化权重
w1 = np.random.randn(D_in, H) #1*64
w2 = np.random.randn(H, D_out) #64*1
# 定义学习率learning_rate
learning_rate = 1e-3
for t in range(500000):
# 进行前向传播
h = x.dot(w1)
h_relu = sigmoid(h)
y_pred = h_relu.dot(w2)#本质这里输出层不需要使用激活函数输出
# 计算损失函数
loss = np.square(y_pred - y).sum()#这里是使用均方差来作为损失函数,故没有1/2
# 进行反向传播
grad_y_pred = 2.0 * (y_pred - y)#这一步是loss对y_pred求导
grad_w2 = h_relu.T.dot(grad_y_pred)
grad_h = grad_y_pred.dot(w2.T)
grad_h = grad_h*sigmoid_derivative(h_relu)
grad_w1 = x.T.dot(grad_h)
#添加代码计算grad_w1#
# 更新权重
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
if (t%50000==0):
plt.cla()
plt.scatter(x,y)
plt.scatter(x,y_pred)
plt.plot(x,y_pred,'r-',lw=1, label="plot figure")
plt.text(5.0, 2.5, 't=%d:Loss=%.4f' % (t, loss), fontdict={'size': 20, 'color': 'red'})
plt.show()
参考
一文弄懂神经网络中的反向传播法——BackPropagationhttps://www.cnblogs.com/codehome/p/9718611.html