概率论基础1----事件

1.Introduction

本系统梳理一下概率论的基础，主要基于"Head First Statistics"【1】和MIT “Introduction to Probability”。第一个部分从统计入手，梳理事件相关的特性。

2.统计班级身高

统计一个大学班级的身高，测量每个人的身高，绘制成下面的表格。

2.1样本空间（sample space）

这个班级里的所有人是这次实验的样本，组成了一个样本空间（sample space）。

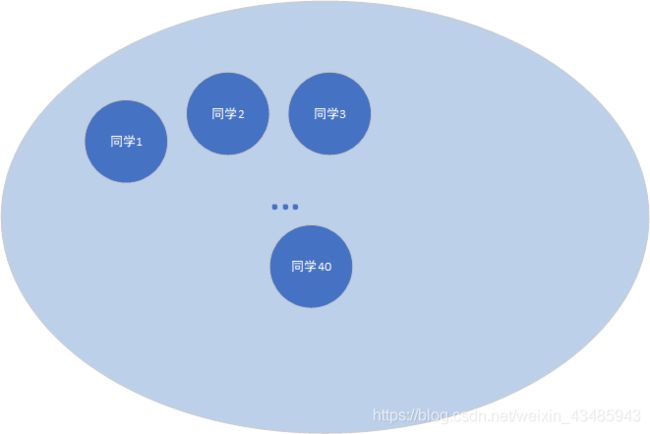
2.2 事件

每个sample对应（变量h）的结果是一个小事件，x1,x2,x3,x4则是更大一点的事件。
按照身高h，可以将sample space划分成下图。

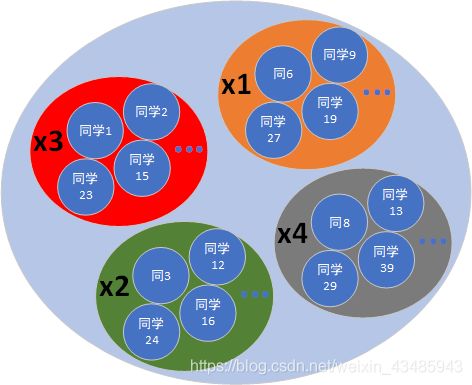
2.3 随机变量（random variable）

事件需要用数学语言进行描述，采用随机变量表示事件，例如如果我们感兴趣的是班级所有学生（样本空间）的身高（随机变量）的规律。

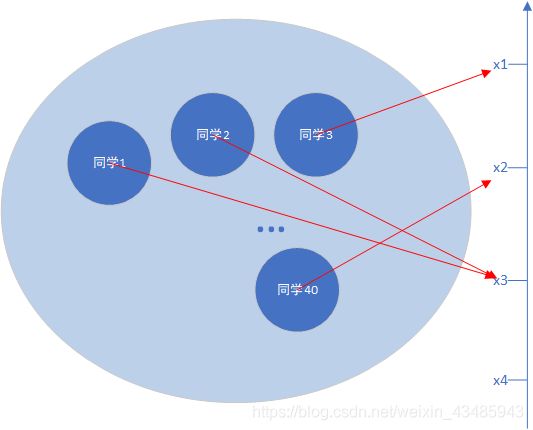
2.3.1 概率

关于概率的定义有很多方式，参见[3]。这里采用贝叶斯观点进行描述。关心每类身高（每类事件x1,x2,…）在sample space中的占比，拿到这个占比以后，在估算下一个班级时，这个占比，就是我们的置信度belief。
$$P_X(x_1)=\frac{x1对应的samples}{samplespace}\text{\hspace{1em}(2.1)}$$

2.3.2 离散事件概率

如果我们关心的是学生的身高段的规律，那么样本和变量数值的对应关系是离散的，计算概率的时候，直接用公式2.1，找到变量对应的样本和样本空间的大小即可以求解。

判断是否是离散事件，主要根据变量是否是离散进行判断（跟对应的样本空间无关），如某人早上从8：00-9：00随机时间去班车等候去，班车有其发车表，他乘坐某次班车的规律如下。虽然对应的班车是一个连续的样本集，但是对应的变量是离散的，乘坐班车还是离散事件。

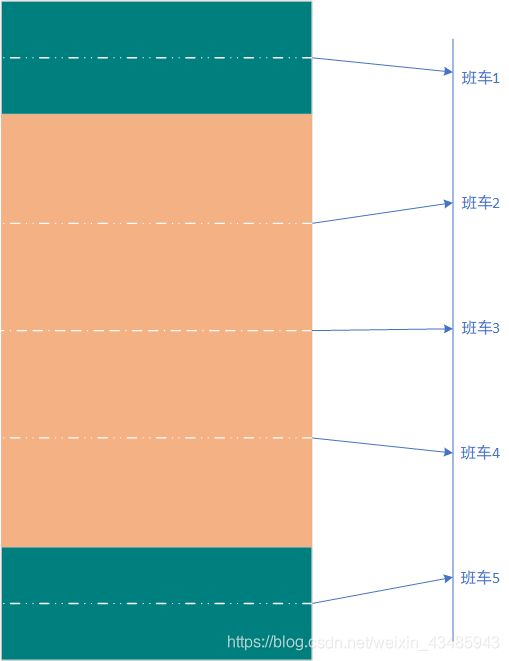
2.3.3 连续事件概率

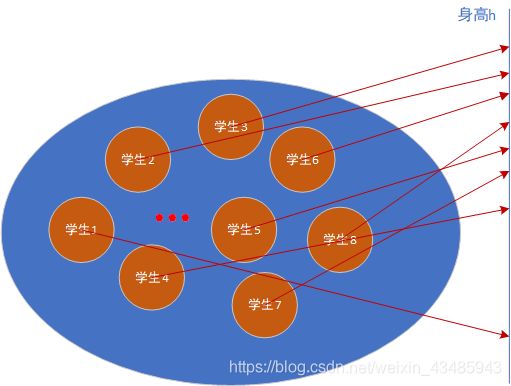
一个班级学生的身高数值是可能是任意的一个点，可以用下面的图表示，每个特殊的身高值对应的概率都是很低的。连续区间的概率才是有意义的，如。
$$P(170<X<180)\frac{区间对应的samples}{samplespace}\text{\hspace{1em}(2.2)}$$

2.3.4 变量之间的关系

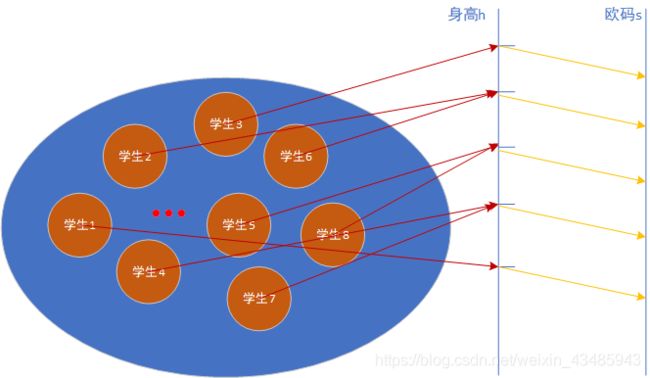
建立变量以后，各种变量之间的关系就利用上了，但是最根本的还是样本空间以及事件到底对应哪些样本。
如班级定做衣服大小的事件，在计算具体某码数对应的概率时，先通过对应的身高h，找到对应的样本。复杂一点的情况，多个不同的h1,h2,产生相同的s=g(h1)和s=g（h2），计算事件s对应的样本是h1和h2对应样本之和。

2.4 通过概率解决一般问题的思路

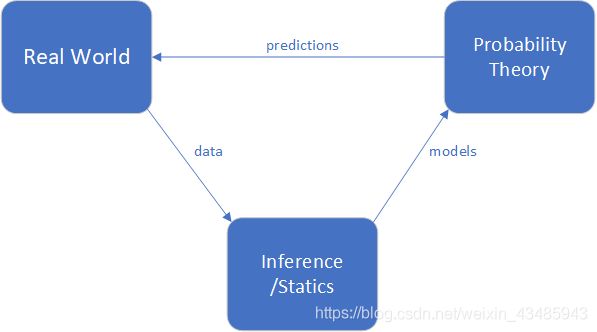
先通过小样本进行试验，获取统计数据，根据统计数据，得到belief（probability），然后根据belief进行预测（主要依据大数定律）。

2.4.1概率相关的变量

根据公式2.1，为了计算事件对应的概率，需要统计事件$X=x_i$对应的samples（统计中的计数问题）；有时候整个的samples space并不能拿到，只能拿到部分的space，涉及到了贝叶斯条件概率问题。

2.5 统计中的计数问题

2.5.1 排列问题

有n个samples，需要将这些samples进行排序，所能得到的全部结果为：
$$num=n!$$

2.5.2 combination 问题

典型的问题1，有40个同学，分成4个group，有多少种分法？
$$num=\frac{40!}{10!10!10!10!}$$
思路：先按照排列的顺序排列好，切成四组，每组全给洗牌掉（10!洗成1）

典型的问题2，有40个同学，取10个，参加比赛，有多少种排列方法？
$$\left(\genfrac{}{}{0ex}{}{40}{10}\right)=\frac{40!}{10!(40-30)!}$$

2.6 贝叶斯条件概率

现在把统计身高扩展到全系，一般在每个班级上进行统计，最后进行汇总。

2.6.1 计算子集的概率

$$P(x_1|1班)=\frac{x_1\cap 一班}{一班}$$
从样本空间的角度去理解，P(A|B)中表示的是当前事件A的样本空间是B。
$$P(A)=P(A|samplespace)=\frac{P(Ainsamplespace)}{P(samplespace)}=P(Ainsamplespace)$$

2.6.2 得到整体的事件概率

$$P(x1)=P(1班)P(x1|一班)+P(2班)P(x1|2班)+P(3班)P(x1|3班)+P(4班)P(x1|4班)$$

2.6.3 贝叶斯条件概率和独立事件

如果两个事件之间有相互关系，如肥胖和高血压之间有一定关系，这个关系如果用概率表述，只要知道肥胖率就可以推导高血压率。
如果是毫不相关的事件，从概率上定义如下
$$P(A|B)=P(A|SampleSpace)$$

References

[1] Dawn Griffiths. “Head First Statistics.” oreilly vlg gmbh & co (2009).
[2] https://ocw.mit.edu/resources/res-6-012-introduction-to-probability-spring-2018/
[3] https://www.zhihu.com/question/26895086