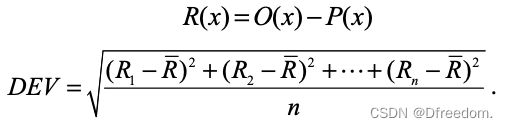光谱数据处理及定量分析
目录
1、光谱简介
2、化学计量学简介
3、光谱数据处理流程(以拉曼光谱为例)
4、数据预处理
4.1 归一化
4.2 滤波
4.3基线校正
5、特征量提取
6、建立数学模型(回归)
1、光谱简介
光是一种由各种波长(或频率)的电磁波叠加起来的电磁辐射。光谱借助光栅、棱镜、傅里叶变换等分光手段将一束电磁辐射的某项性质解析成辐射的各个组成波长对此性质贡献的图表。
2、化学计量学简介
化学计量学是综合运用计算机科学、数学和统计学等相关学科,寻找最佳方法优化化学测量过程,并从测量数据中最大限度地提取有用信息。将化学计量学与分子光谱相结合,最大限度地提取光谱数据中的有用信息,建立对分析组分性质高效、可靠的分析检测模型。
3、光谱数据处理流程(以拉曼光谱为例)
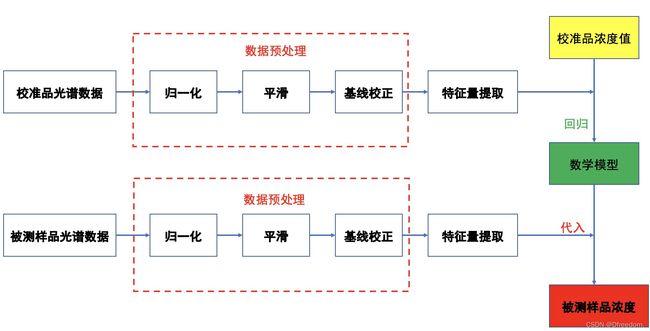
拉曼光谱用于定量分析的处理流程如下:
对于一个测量系统来说,算法的流程分为两条线路,一条是提取已知的样品(校准品)的特征量,然后通过回归算法在特征量与浓度之间建立一个数学模型,一条是提取被测样品的特征量,然后再代入数学模型中计算得到被测样品的浓度值。
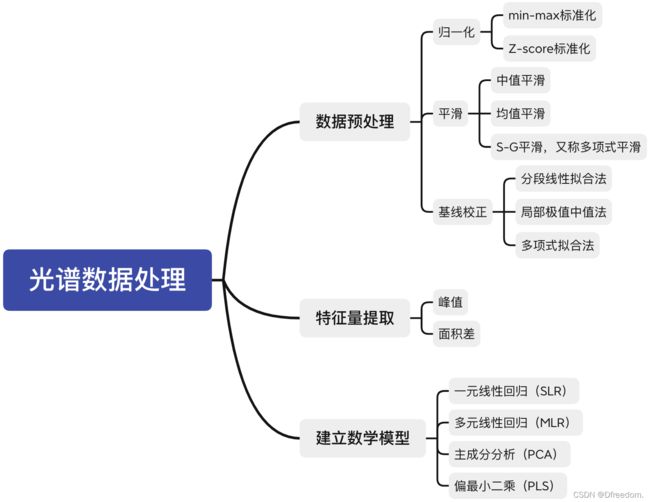
从上述的流程中可以将光谱算法分为三大块:数据预处理、特征量提取、建立数学模型。常见的算法整理如下:
4、数据预处理
4.1 归一化
原因:不同条件下采集到的光谱数据往往具有不同的量纲和量纲单位,这样的情况会影响到数据分析的结果
方法:采用归一化的算法使数据被限定在一定的范围内比如[0,1]或者[-1,1]),从而让不同浓度的光谱数据具有可比性。常用的归一化算法有以下两种:
(1)min-max标准化(Min-Max Normalization)(线性函数归一化)
本质:把数变为【0,1】之间的小数。
转换函数:(X-Min)/(Max-Min)
其中,X为原始数据,Min所有样本数据的最小值,Max为所有样本数据的最大值。
(2)0均值标准化(Z-score standardization)
本质:把有量纲表达式变成无量纲表达式。
转换函数:(X-Mean)/SD
其中,Mean为所有样本数据的均值。SD为所有样本数据的标准差。
| 序号 |
归一化方法 |
应用场景 |
缺点 |
| 1 |
Min-Max Normalization |
不涉及距离度量、协方差计算、数据不符合正太分布的时候 |
(1)当有新数据加入时,会导致min(x)和max(x)的变化,需要重新定义; (2)存在极端的最大值或者最小值。 |
| 2 |
z—score 标准化 |
1、在分类、聚类算法中,需要使用距离来度量相似性的时候; 2、使用PCA技术进行降维的时候; 3、数据服从正态分布 |
/ |
4.2 滤波
原因:光谱数据中存在随机噪声(光源噪声、CCD噪声、暗电流等),同样会影响后续的数据分析结果。
方法:采用数字滤波算法滤除随机噪声,提高信噪比。常用的滤波算法有滑动中值滤波、滑动均值滤波、滑动多项式滤波(Savitzky-Golay滤波 )等
(1)滑动中值滤波
原理:采用一个窗口沿着光谱向量平移,逐一求取窗口内元素的中值,替代原始光谱中窗口中心位置处的元素,即可得到降噪的光谱。
MATLAB代码:
yy=medfilt1(y,framelen)
Yy为输出,y为输入,framelen为窗口长度;
(2)滑动均值滤波
原理:采用一个窗口沿着光谱向量平移,逐一求取窗口内元素的均值,替代原始光谱中窗口中心位置处的元素,即可得到降噪的光谱。
MATLAB代码:
yy=smooth(y,span);
%span为奇数,表示窗宽,比如span=2,则窗口长度为5;
(3)滑动多项式滤波(S-G滤波)
原理:通过一个移动窗口,对窗口内部元素做多项式最小二乘拟合,得到窗口中 心位置处元素平滑后的值。
MATLAB代码:
yy = sgolayfilt(y,order,framelen)
% order为多项式阶数,framelen为窗口长度。
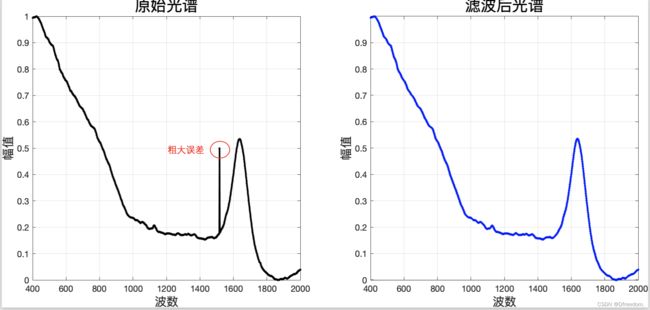
滤波效果:
4.3基线校正
原因:荧光背景、样品及周围环境的黑体辐射等影响,导致光谱的基线产生,其表现为缓慢变化曲线,直接对后续的数据分析产生影响。因此需要在后续处理之前将谱线中的基线消除。
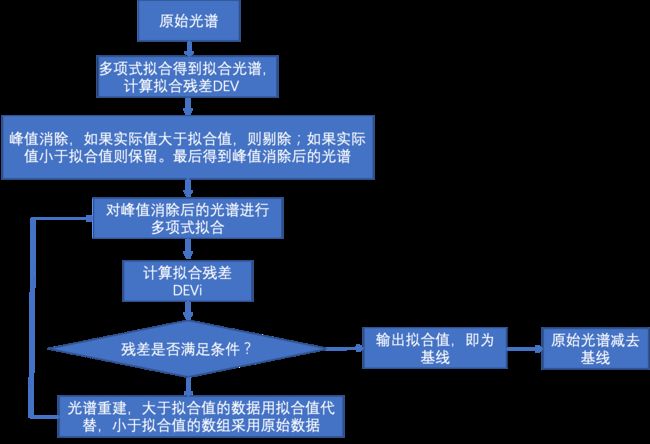
常用的基线校正算法有分段线性拟合法、局部极值中值法、多项式拟合法。本文主要介绍多项式拟合法。多项式拟合的实现流程如下:
分三步:
① 峰值消除;
② 多项式拟合逼近基线,得到基线;
③ 减去基线,得到基线校正后的光谱数据。
其中,拟合残差计算公式如下:
式中O(x)为原始光谱,P(x)为拟合光谱,DEV为残差。
残差判断条件如下:
If i=1,判断条件为abs(DEV1-DEV)/DEV1<0.05;
else,判断条件为abs(DEVi-DEVi-1)/DEVi<0.05;
MATLAB代码:
x=[];%拉曼位移
y=[];%原始光谱
n=5;%多项式阶数
[p0,s0,mu0]=polyfit(x,y,n);%多项式拟合
y_fit0=polyval(p0,x,[],mu0);%计算拟合值
r0=y-y_fit0;
dev0=sqrt(sum((r0-mean(r0)).^2)/length(r0));%计算残差
y_remove0=y(find(y<=y_fit0));%峰值消除
x_remove0=x(find(y<=y_fit0));%峰值消除
i=1;
judge=1;
while(judge)
p1,s1,mu1]=polyfit(x_remove0,y_remove0,n);%多项式拟合
y_fit1=polyval(p1,x_remove0,[],mu1);%计算拟合值
r1=y_remove0-y_fit1;
dev(i)=sqrt(sum((r1-mean(r1)).^2)/length(r1));%计算残差
if i==1
judge=abs(dev(i)-dev0)/dev(i)>0.05;
else
judge=abs((dev(i)-dev(i-1))/dev(i))>0.05;%残差判断条件
end
index=find(y_remove0<=y_fit1);
y_remove0(index)=y_fit1(index);%光谱重建,大于拟合值的数据用拟合值代替,小于拟合值的数组采用原始数据
i=i+1
end
y_baseline=polyval(p1,x,[],mu1);%基线
y_baseline_correction=y-y_baseline;%基线校正后
figure(1)
h=plot(x,y,'k',x,y_baseline,'r',x,y_baseline_correction,'b')
set(h,'Linewidth',2,'Markersize',2)%设置线宽和点的大小
title('基线校正效果','fontsize',20)%图形标题
xlabel('波数','fontsize',15)%x轴名称
ylabel('幅值','fontsize',15)%y轴名称
grid on %打开网格线
egend('原始光谱','基线','基线校正后的光谱')%添加图例
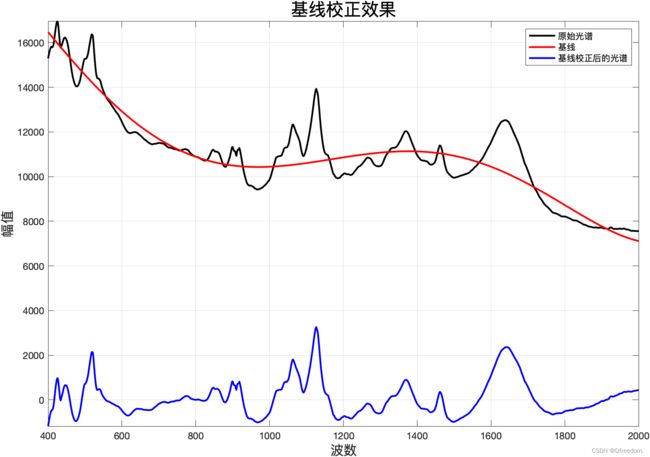
axis tight基线校正效果:
5、特征量提取
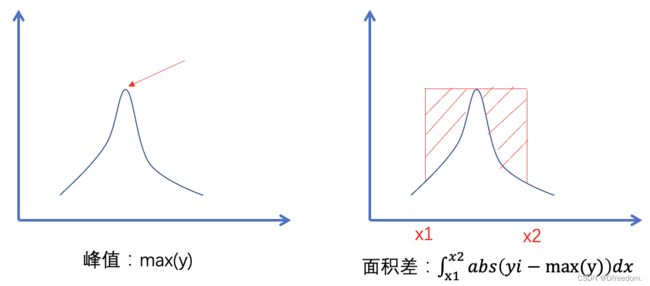
为了提取和浓度有一定函数关系的特征量,最常用的是谱线的峰值或者谱线与坐标轴所夹的面积差。
6、建立数学模型(回归)
求解得到特征量与浓度值的函数关系式,一般采用回归的方式。
MATLAB代码:
PCR:主成分分析(PCA)原理分析&Python实现_Dfreedom.的博客-CSDN博客_pca python
PLS:偏最小二乘(PLS)原理分析&Python实现_Dfreedom.的博客-CSDN博客_偏最小二乘回归分析python