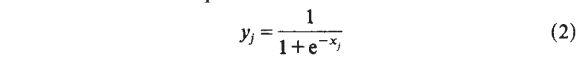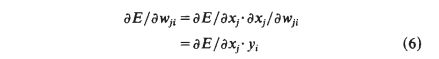深度学习论文 Learning representations by back-propagating errors
Learning representations by back-propagating errors
小记
2022.3.16 第一次读全英语论文
看了吴恩达的课之后明白了BP原理,但是还是想看看原论文是怎么写的。
论文最后的那个图fig的解释看的云里雾里的,以后看多了再回来补。
论文下载:http://www.cs.toronto.edu/~hinton/absps/naturebp.pdf
参考博客
[BP系列]-Learning representations by back-propagating errors_Dream__Zh的博客-CSDN博客 借鉴博主思路
抽点时间读经典AI论文之Learning representations by back-propagating errors_Mr.郑先生_的博客-CSDN博客
大佬用excel演示了BP过程,大佬看论文的方式值得借鉴!
论文内容
前言 :简略介绍模型原理
1.1 We describe a new learning procedure, back-propagation, for networks of neurone-like units.
提出了一种新的学习过程,反向传播,为类神经元单元的网络。
文章讲什么
1.2 The procedure repeatedly adjusts the weights of the connections in the network so as to minimize a measure of the difference between the actual output vector of the net and the desired output vector.
该程序反复调整网络中连接的权值,以最小化网络的实际输出向量和期望输出向量之间的差值的度量。
文章的模型特点1
1.3 As a result of the weight adjustments, internal ‘hidden’ units which are not part of the input or output come to represent important features of the task domain, and the regularities in the task are captured by the interactions of these units.
权重的调整,使得不属于输入或输出的内部“隐藏”单元能够表达任务领域的重要特征,同时这些任务中的规律也能被这些单元的交互所捕获。
模型特点2
研究背景 :使用隐层构建复杂学习模型
2.1
If the input units are directly connected to the output units it is relatively easy to find learning rules that iteratively adjust the relative strengths of the connections so as to progressively reduce the difference between the actual and desired output vectors.
如果输入单元直接连接到输出单元,则权值调整的规则比较简单。
说明直接连接不能构建复杂学习模型,故而要隐层。
2.2
Learning becomes more interesting but more difficult when we introduce hidden units whose actual or desired states are not specified by the task. (In perceptrons, there are ‘feature analysers’ between the input and output that are not true hidden units because their input connections are fixed by hand, so their states are completely determined by the input vector: they do not learn representations.)
当引入隐层时,学习过程也变得更复杂了。(在感知器中,输入和输出之间存在着“特征分析器”,它们不是真正的隐藏单元,因为它们的输入连接是手工固定的,所以它们的状态完全是由输入向量决定的:它们不学习表示。)
❓我有疑惑点,隐藏层是手动连接的就不算真正的隐层?我现在初学,以为中间层都是隐层。
2.3
The learning procedure must decide under what circumstances the hidden units should be active in order to help achieve the desired input-output behaviour. This amounts to deciding what these units should represent.
学习过程会决定什么情况下隐层单元被激活,才能让输出与输入符合。这也意味着学习过程将知道这些隐层单元表示的是什么。
2.4
We demonstrate that a general purpose and relatively simple procedure is powerful enough to construct appropriate internal representations.
作者证明了一个可以有通用目的,且过程相对简单而足够强大的学习模型的内部表达。
引出为什么要介绍这个模型
模型结构: 多层
3.1
The simplest form of the learning procedure is for layered networks which have a layer of input units at the bottom; any number of intermediate layers; and a layer of output units at the top. Connections within a layer or from higher to lower layers are forbidden, but connections can skip intermediate layers.
一个学习过程的最简单形式是分层网络,它在底部有一层输入单元;任意数量的中间层;顶部有一层输出单元。禁止在一个层内或从高层到下层的连接(单向的),但是连接可以跳过中间层。
3.2-5.1
An input vector is presented to the network by setting the states of the input units. Then the states of the units in each layer are determined by applying equations (1) and (2) to the connections coming from lower layers. All units within a layer have their states set in parallel, but different layers have their states set sequentially, starting at the bottom and working upwards until the states of the output units are determined.
The total input, x i x_i xi, to unit j is a linear function of the outputs, y i y_i yi, of the units that are connected to j and of the weights, w j i w_{ji} wji on these connections
x j = ∑ y i w j i x_j=\sum{y_i w_{ji}} xj=∑yiwji Units can be given biases by introducing an extra input to each unit which always has a value of 1. The weight on this extra input is called the bias and is equivalent to a threshold of the opposite sign. It can be treated just like the other weights.
A unit has a real-valued output, Yi, which is a non-linear function of its total input
x j x_j xj 是本层第j 个单元的输入, y i y_i yi 是上一层第i 个单元的输出。
第 l 层的某单位元的输入是第 l-1 层神经元的线性组合 x j = ∑ y i w j i x_j=\sum{y_i w_{ji}} xj=∑yiwji ,而输出是经过非线性函数(激活函数)的结果,如 y j = 1 1 + e − x j y_j=\frac{1}{1+e^{-x_j}} yj=1+e−xj1。
❓ 激活函数是什么时候提出的呢
激活函数
5.2
It is not necessary to use exactly the functions given in equations (1) and (2). Any input-output function which has a bounded derivative will do. However, the use of a linear function for combining the inputs to a unit before applying the nonlinearity greatly simplifies the learning procedure.
不是得确定地用 x j = ∑ y i w j i x_j=\sum{y_i w_{ji}} xj=∑yiwji和 y j = 1 1 + e − x j y_j=\frac{1}{1+e^{-x_j}} yj=1+e−xj1中两个函数。任何有有界导数的输入输出函数都可以。但是在要选择一个能归一化的非线性激活函数。
激活函数的选择原则
误差
6.1
The total error, E, is defined as
, where c is an index over cases (input-output pairs), j is an index over output units, y is the actual state of an output unit and d is its desired state.
To minimize E by gradient descent it is necessary to compute the partial derivative of E with respect to each weight in the network. This is simply the sum of the partial derivatives for each of the input-output cases, For a given case, the partial derivatives of the error with respect to each weight are computed in two passes. We have already described the forward pass in which the units in each layer have their states determined by the input they receive from units in lower layers using equations (1) and (2). The backward pass which propagates derivatives from the top layer back to the bottom one is more complicated.
总体误差 E = 1 2 ∑ c ∑ j ( y j , c − d j , c ) 2 E=\frac{1}{2}\sum_c \sum_j(y_{j,c}-d_{j,c})^2 E=21∑c∑j(yj,c−dj,c)2 , c代表样本序号,j 代表输出单元的序号[一个样本输出的维数], y y y代表网络实际输出, d d d 代表所希望的输出。
为了通过梯度下降法减少总体误差E ,需要计算E 关于网络中所有权值的偏导。对于一个给定的样本,有两种方式计算其偏导,一种是从低层向高层传递,我们称之为前向传递;另一种从顶层向低层反向传导的算法,则更为复杂
为了通过梯度下降来最小化E,需要计算E对网络中每个权值的偏导数。这只是每个输入-输出情况下的偏导数的和,对于一个给定的情况,相对于每个权重的误差的偏导数在两次传递中计算。我们已经用方程(1)和(2)描述了每一层的单元的正向传递,其中这些单元的状态由它们从较下层的单元接收到的输入决定。将导数从顶层传播到底层的反向传递更为复杂。
反向传播原理
7
The backward pass starts by computing ∂ E ∂ y \frac{\partial ^ E}{\partial y} ∂y∂Efor each of the output units. Differentiating equation (3) for a particular case, c, and suppressing the index c gives
We can then apply the chain rule to compute ∂ E ∂ x j \frac{\partial ^ E}{\partial x_j} ∂xj∂E,
![]()
Differentiating equation (2) to get the value of d y j d x j \frac{\mathrm{d} y_j }{\mathrm{d} x_j} dxjdyj and substituting gives
![]()
This means that we know how a change in the total input x to an output unit will affect the error. But this total input is just a linear function of the states of the lower level units and it is also a linear function of the weights on the connections, so it is easy to compute how the error will be affected by changing these states and weights. For a weight w j i w_{ji} wji, from i to j the derivative is
and for the output of the i t h i^{th} ith unit the contribution to ∂ E ∂ y i \frac{\partial ^ E}{\partial y_i} ∂yi∂E ,resulting from the effect of i on j is simply
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jNLVSrvW-1647523988920)(C:\Users\29066\AppData\Roaming\Typora\typora-user-images\image-20220317180954198.png)]
so taking into account all the connections emanating from unit i we have
这部分我在吴恩达的视频里看懂了,所以这边就简单做个笔记
权值更新
反向传播完了之后,就要根据误差值修改权值
8.1
One way of using ∂ E ∂ w \frac{\partial E}{\partial w} ∂w∂E is to change the weights after every input-output case. This has the advantage that no separate memory is required for the derivatives. An alternative scheme, which we used in the research reported here, is to accumulate ∂ E ∂ w \frac{\partial E}{\partial w} ∂w∂E over all the input-output cases before changing the weights.
一种方式是,针对每一个样本计算梯度,更新权值。该方法的优点是,不需要额外的存储空间存储梯度向量。另一种方案,也是本文中所使用的方案,是将所有样本的梯度进行累积后,统一更新。
8.2
The simplest version of gradient descent is to change each weight by an amount proportional to the accumulated ∂ E ∂ w \frac{\partial E}{\partial w} ∂w∂E
This method does not converge as rapidly as methods which make use of the second derivatives, but it is much simpler and can easily be implemented by local computations in parallel hardware. It can be significantly improved, without sacrificing the simplicity and locality, by using an acceleration method in which the current gradient is used to modify the velocity of the point in weight space instead of its position
![]()
where t is incremented by 1 for each sweep through the whole set of input-output cases, and a is an exponential decay factor between O and 1 that determines the relative contribution of the current gradient and earlier gradients to the weight change.
最简单的梯度下降法的下降向量是是(8),尽管易于实现却收敛很慢。
故对(8)改进提出(9)。
其中, α \alpha α 是一个在( 0 , 1 ) (0,1)(0,1) 之间的指数衰减因子,它确定了当前梯度和先前梯度对权重更新的相对贡献。
实验验证
这部分真没看懂,请教大佬
9
To break symmetry we start with small random weights. Variants on the learning procedure have been discovered independently by David Parker (personal communication) and by Yann Le Cun3.
One simple task that cannot be done by just connecting the input units to the output units is the detection of symmetry. To detect whether the binary activity levels of a one-dimensional array of input units are symmetrical about the centre point, it is essential to use an intermediate layer because the activity in an individual input unit, considered alone, provides no evidence about the symmetry or non-symmetry of the whole input vector, so simply adding up the evidence from the individual input units is insufficient. (A more formal proof that intermediate units are required is given in ref. 2.) The learning procedure discovered an elegant solution using just two intermediate units, as shown in Fig. 1.
Another interesting task is to store the information in the two family trees (Fig. 2). Figure 3 shows the network we used, and Fig. 4 shows the ‘receptive fields’ of some of the hidden units after the network was trained on 100 of the 104 possible triples.
So far, we have only dealt with layered, feed-forward networks. The equivalence between layered networks and recurrent networks that are run iteratively is shown in Fig. 5.
读后收获
-
英语单词收获:perceptron 感知器, back-propagating 反向传播
-
我对隐层的概念以后还是要注意,文章中提出自行联结的隐层不是真正的隐层,以后我具体实现的时候再回来回答这个问题 ❓
-
激活函数原来早在这篇文章1986年之前就有了这个概念,还是很好奇是怎么提出激活函数的
-
对BP模型的结构更深刻了,顶层输出,底层输入,中间有无数层,层内不可联,层间单向。
-
这个概念对我也很重要:学习过程会决定什么情况下隐层单元被激活,才能让输出与输入符合。这也意味着学习过程将知道这些隐层单元表示的是什么特征