NNDL 实验三 线性回归

使用pytorch实现

2.2 线性回归

2.2.1 数据集构建

构造一个小的回归数据集：

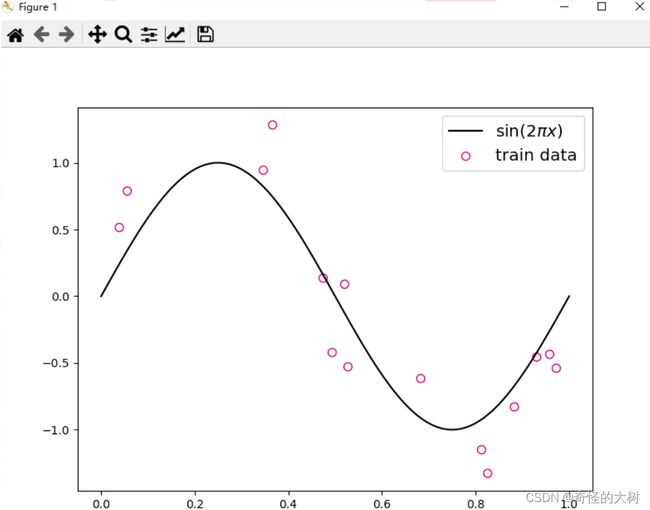
生成 150 个带噪音的样本，其中 100 个训练样本，50 个测试样本，并打印出训练数据的可视化分布。

import numpy as np
import torch
import pandas as pd
import matplotlib.pyplot as plt
def creat_data(w,b,num_examples):
    x = torch.normal(0,1,(num_examples,len(w)))
    '''
    标准正态分布，对应于np.random.normal(loc=0, scale=1, size=shape)
    参数loc(float)：正态分布的均值，对应着这个分布的中心。loc=0说明这一个以Y轴为对称轴的正态分布，
    参数scale(float)：正态分布的标准差，对应分布的宽度，scale越大，正态分布的曲线越矮胖，scale越小，曲线越高瘦。
    参数size(int 或者整数元组)：输出的值赋在shape里，默认为None
    '''
    y = np.matmul(x, w) + b
    # numpy.matmul 函数返回两个数组的矩阵乘积。当两个数组都是二维数组的时候，就是数学上的两个矩阵的乘积。
    return x,y.reshape(-1,1)
    # numpy.reshape(-1,1)，将原来的数据，改为1列（注意reshape的1），但是行数不确定，numpy库自己计算（注意reshape的-1）。
# 添加噪声
def get_noise(loc,scale,y):
    noise = torch.normal(loc,scale,y.shape)
    return y + noise

true_w = [1.2]
true_b = 0.5
features, labels = creat_data(true_w, true_b, 150)
# 增加噪声
labels = get_noise(0,0.1,labels)
train_features = features[0:100]
train_labels = labels[0:100]
test_features = features[100:150]
test_labels = labels[100:150]

# 图像展示
plt.figure(1)
plt.scatter(train_features,train_labels,c='r')
plt.show()

2.2.2 模型构建

import torch
from op import Op

torch.manual_seed(10) # 设置随机种子

# 线性算子
class Linear(Op):
    def __init__(self, input_size):
        """
        输入：
           - input_size:模型要处理的数据特征向量长度
        """

        self.input_size = input_size

        # 模型参数
        self.params = {}
        self.params['w'] = torch.randn(self.input_size, 1)
        self.params['b'] = torch.zeros(size=[1], dtype=torch.float32)

    def __call__(self, X):
        return self.forward(X)

    # 前向函数
    def forward(self, X):
        """
        输入：
           - X: tensor, shape=[N,D]
           注意这里的X矩阵是由N个x向量的转置拼接成的，与原教材行向量表示方式不一致
        输出：
           - y_pred： tensor, shape=[N]
        """

        N, D = X.shape

        if self.input_size == 0:
            return torch.full(shape=[N, 1], fill_value=self.params['b'])

        assert D == self.input_size  # 输入数据维度合法性验证

        # 使用paddle.matmul计算两个tensor的乘积
        y_pred = torch.matmul(X, self.params['w']) + self.params['b']

        return y_pred

input_size = 3
N = 2
X = torch.randn(N, input_size)  # 生成2个维度为3的数据
model = Linear(input_size)
y_pred = model(X)
print("y_pred:", y_pred)  # 输出结果的个数也是2个

y_pred: tensor([[1.8529],
        [0.6011]])

2.2.3 损失函数

回归任务中常用的评估指标是均方误差

均方误差（mean-square error, MSE）是反映估计量与被估计量之间差异程度的一种度量。
 

import torch

def mean_squared_error(y_true, y_pred):
    """
    输入：
       - y_true: tensor，样本真实标签
       - y_pred: tensor, 样本预测标签
    输出：
       - error: float，误差值
    """

    assert y_true.shape[0] == y_pred.shape[0]

    error = torch.mean(torch.square(y_true - y_pred))

    return error

# 构造一个简单的样例进行测试:[N,1], N=2
y_true = torch.tensor([[-0.2], [4.9]], dtype=torch.float32)
y_pred = torch.tensor([[1.3], [2.5]], dtype=torch.float32)

error = mean_squared_error(y_true=y_true, y_pred=y_pred).item()
print("error:", error)

error: 4.005000114440918

进程已结束，退出代码为 0

思考：没有除2是不影响的，代码中没有除以二，损失函数公式中含有平方，在之后对其进行求导，会多出一个二，所以公式中除以二以简化求导后的结果

2.2.4 模型优化

经验风险 （ Empirical Risk ），即在训练集上的平均损失。

def optimizer_lsm(model, X, y, reg_lambda=0):
    '''
      输入：
         - model: 模型
         - X: tensor, 特征数据，shape=[N,D]
         - y: tensor,标签数据，shape=[N]
         - reg_lambda: float, 正则化系数，默认为0
      输出：
         - model: 优化好的模型
      '''
    N, D = X.shape
    # 对输入特征数据所有特征向量求平均
    x_bar_tran = torch.mean(X,0).T
    # 求标签的均值,shape=[1]
    y_bar = torch.mean(y)
    # torch.subtract通过广播的方式实现矩阵减向量
    x_sub = torch.subtract(X, x_bar_tran)
    # 使用torch.all判断输入tensor是否全0
    if torch.all(x_sub == 0):
        model.params['b'] = y_bar
        model.params['w'] = torch.zeros([D])
        return model

    # torch.inverse求方阵的逆
    tmp = torch.inverse(torch.matmul(x_sub.T, x_sub) +
                         reg_lambda * torch.eye(D))
    w = torch.matmul(torch.matmul(tmp, x_sub.T), (y - y_bar))
    b = y_bar - torch.matmul(x_bar_tran, w)
    model.params['b'] = b
    model.params['w'] = torch.squeeze(w, -1)
    return model

思考：
1.省略1/N不影响，1为N维的全一向量。
2.最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用它可以求得的数据，使这些数据与实际数据之间误差的平方和最小

2.2.5 模型训练

在准备了数据、模型、损失函数和参数学习的实现之后，开始模型的训练。

在回归任务中，模型的评价指标和损失函数一致，都为均方误差。

通过上文实现的线性回归类来拟合训练数据，并输出模型在训练集上的损失。

input_size = 1
model = Linear(input_size)
model = optimizer_lsm(model,X_train.reshape([-1,1]),y_train.reshape([-1,1]))
print("w_pred:", model.params['w'].item(), "b_pred: ", model.params['b'].item())
y_train_pred = model(X_train.reshape([-1,1])).squeeze()
train_error = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()
print("train error: ", train_error)

w_pred: 1.2271720170974731 b_pred:  0.37986236810684204
train error:  3.632181406021118

model_large = Linear(input_size)
model_large = optimizer_lsm(model_large,X_train_large.reshape([-1,1]),y_train_large.reshape([-1,1]))
print("w_pred large:",model_large.params['w'].item(), "b_pred large: ", model_large.params['b'].item())
y_train_pred_large = model_large(X_train_large.reshape([-1,1])).squeeze()
train_error_large = mean_squared_error(y_true=y_train_large, y_pred=y_train_pred_large).item()
print("train error large: ",train_error_large)

w_pred large: 1.1993682384490967 b_pred large:  0.5421561002731323
train error large:  3.9921984672546387

2.2.6 模型评估

用训练好的模型预测一下测试集的标签，并计算在测试集上的损失。

y_test_pred = model(X_test.reshape([-1,1])).squeeze()
test_error = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()
print("test error: ",test_error)

test error:  4.306798458099365

y_test_pred_large = model_large(X_test.reshape([-1,1])).squeeze()
test_error_large = mean_squared_error(y_true=y_test, y_pred=y_test_pred_large).item()
print("test error large: ",test_error_large)

test error large:  4.420894622802734

---

2.3 多项式回归

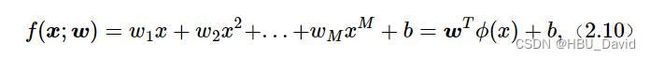
2.3.1 数据集构建

构建训练和测试数据，其中：

# sin函数: sin(2 * pi * x)
def sin(x):
    y = torch.sin(2 * math.pi * x)
    return y
# 生成数据
func = sin
interval = (0,1)
train_num = 15
test_num = 10
noise = 0.5 #0.1
X_train, y_train = create_toy_data(func=func, interval=interval, sample_num=train_num, noise = noise)
X_test, y_test = create_toy_data(func=func, interval=interval, sample_num=test_num, noise = noise)

X_underlying = torch.linspace(interval[0],interval[1],100)
y_underlying = sin(X_underlying)

# 绘制图像
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
#plt.scatter(X_test, y_test, facecolor="none", edgecolor="r", s=50, label="test data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.legend(fontsize='x-large')
plt.savefig('ml-vis2.pdf')
plt.show()

 

训练数样本 15 个，测试样本 10 个，高斯噪声标准差为 0.1，自变量范围为 (0,1)。

2.3.2 模型构建

# 多项式转换
def polynomial_basis_function(x, degree=2):
    """
    输入：
       - x: tensor, 输入的数据，shape=[N,1]
       - degree: int, 多项式的阶数
       example Input: [[2], [3], [4]], degree=2
       example Output: [[2^1, 2^2], [3^1, 3^2], [4^1, 4^2]]
       注意：本案例中,在degree>=1时不生成全为1的一列数据；degree为0时生成形状与输入相同，全1的Tensor
    输出：
       - x_result： tensor
    """
    if degree == 0:
        # x = torch.ones(x.shape)
        # x = x.to(torch.float32)
        # return x
        return torch.ones(x.shape)
    x_tmp = x
    x_result = x_tmp
    for i in range(2, degree + 1):
        x_tmp = torch.mul(x_tmp, x)  # 逐元素相乘
        x_result = torch.cat((x_result, x_tmp), dim=-1)
    return x_result

# 简单测试
data = [[2], [3], [4]]
X = torch.tensor(data=data)
X = X.to(torch.float32)
degree = 3
transformed_X = polynomial_basis_function(X, degree=degree)
print("转换前：", X)
print("阶数为", degree, "转换后：", transformed_X)

转换前： tensor([[2.],
        [3.],
        [4.]])
阶数为 3 转换后： tensor([[ 2.,  4.,  8.],
        [ 3.,  9., 27.],
        [ 4., 16., 64.]])

套用求解线性回归参数的方法来求解多项式回归参数

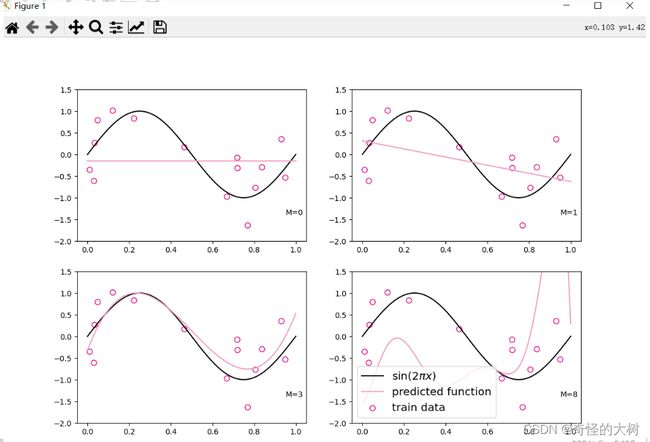
2.3.3 模型训练

plt.rcParams['figure.figsize'] = (12.0, 8.0)

for i, degree in enumerate([0, 1, 3, 8]):  # []中为多项式的阶数
    model = Linear(degree)
    X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), degree)
    X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), degree)
    model = optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))  # 拟合得到参数
    y_underlying_pred = model(X_underlying_transformed).squeeze()
    print(model.params)

    # 绘制图像
    plt.subplot(2, 2, i + 1)
    plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
    plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
    plt.plot(X_underlying, y_underlying_pred, c='#f19ec2', label="predicted function")
    plt.ylim(-2, 1.5)
    plt.annotate("M={}".format(degree), xy=(0.95, -1.4))

# plt.legend(bbox_to_anchor=(1.05, 0.64), loc=2, borderaxespad=0.)
plt.legend(loc='lower left', fontsize='x-large')
plt.savefig('ml-vis3.pdf')
plt.show()

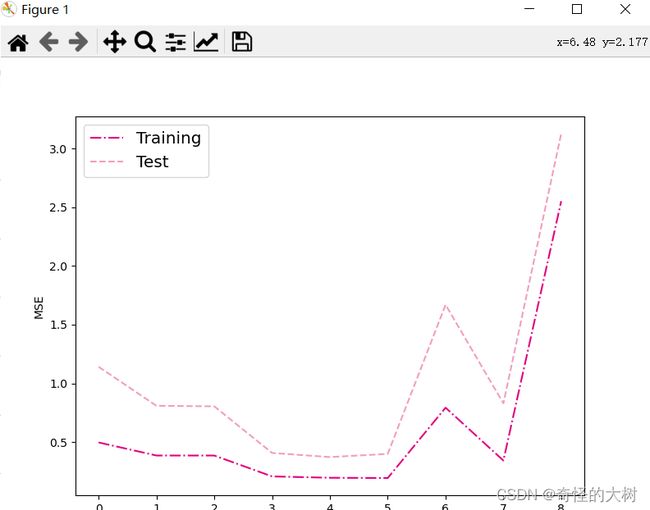
2.3.4 模型评估

# 训练误差和测试误差
training_errors = []
test_errors = []
distribution_errors = []

# 遍历多项式阶数
for i in range(9):
    model = Linear(i)

    X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), i)
    X_test_transformed = polynomial_basis_function(X_test.reshape([-1, 1]), i)
    X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), i)

    optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))

    y_train_pred = model(X_train_transformed).squeeze()
    y_test_pred = model(X_test_transformed).squeeze()
    y_underlying_pred = model(X_underlying_transformed).squeeze()

    train_mse = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()
    training_errors.append(train_mse)

    test_mse = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()
    test_errors.append(test_mse)

    # distribution_mse = mean_squared_error(y_true=y_underlying, y_pred=y_underlying_pred).item()
    # distribution_errors.append(distribution_mse)

print("train errors: \n", training_errors)
print("test errors: \n", test_errors)
# print ("distribution errors: \n", distribution_errors)

# 绘制图片
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.plot(training_errors, '-.', mfc="none", mec='#e4007f', ms=10, c='#e4007f', label="Training")
plt.plot(test_errors, '--', mfc="none", mec='#f19ec2', ms=10, c='#f19ec2', label="Test")
# plt.plot(distribution_errors, '-', mfc="none", mec="#3D3D3F", ms=10, c="#3D3D3F", label="Distribution")
plt.legend(fontsize='x-large')
plt.xlabel("degree")
plt.ylabel("MSE")
plt.savefig('ml-mse-error.pdf')
plt.show()

---

2.4 Runner类介绍

机器学习方法流程包括数据集构建、模型构建、损失函数定义、优化器、模型训练、模型评价、模型预测等环节。

为了更方便地将上述环节规范化，我们将机器学习模型的基本要素封装成一个Runner类。

除上述提到的要素外，再加上模型保存、模型加载等功能。

Runner类的成员函数定义如下：

__init__函数：实例化Runner类，需要传入模型、损失函数、优化器和评价指标等；
train函数：模型训练，指定模型训练需要的训练集和验证集；
evaluate函数：通过对训练好的模型进行评价，在验证集或测试集上查看模型训练效果；
predict函数：选取一条数据对训练好的模型进行预测；
save_model函数：模型在训练过程和训练结束后需要进行保存；
load_model函数：调用加载之前保存的模型。

# Runner类
class Runner(object):
    def __init__(self, model, optimizer, loss_fn, metric):
        self.model = model         # 模型
        self.optimizer = optimizer # 优化器
        self.loss_fn = loss_fn     # 损失函数
        self.metric = metric       # 评估指标
    # 模型训练
    def train(self, train_dataset, dev_dataset=None, **kwargs):
        pass
    # 模型评价
    def evaluate(self, data_set, **kwargs):
        pass
    # 模型预测
    def predict(self, x, **kwargs):
        pass
    # 模型保存
    def save_model(self, save_path):
        pass
    # 模型加载
    def load_model(self, model_path):
        pass

---

2.5 基于线性回归的波士顿房价预测

使用线性回归来对马萨诸塞州波士顿郊区的房屋进行预测。

实验流程主要包含如下5个步骤：

数据处理：包括数据清洗（缺失值和异常值处理）、数据集划分，以便数据可以被模型正常读取，并具有良好的泛化性;
模型构建：定义线性回归模型类；
训练配置：训练相关的一些配置，如：优化算法、评价指标等；
组装训练框架Runner：Runner用于管理模型训练和测试过程；
模型训练和测试：利用Runner进行模型训练和测试。
2.5.1 数据处理

    2.5.1.1数据集

data = pd.read_csv(r'C:\Users\86181\Desktop\boston_house_prices.csv')
print(data.head())

      CRIM    ZN  INDUS  CHAS    NOX  ...  RAD  TAX  PTRATIO  LSTAT  MEDV
0  0.00632  18.0   2.31     0  0.538  ...    1  296     15.3   4.98  24.0
1  0.02731   0.0   7.07     0  0.469  ...    2  242     17.8   9.14  21.6
2  0.02729   0.0   7.07     0  0.469  ...    2  242     17.8   4.03  34.7
3  0.03237   0.0   2.18     0  0.458  ...    3  222     18.7   2.94  33.4
4  0.06905   0.0   2.18     0  0.458  ...    3  222     18.7   5.33  36.2

[5 rows x 13 columns]

    2.5.1.2 数据清洗

# 查看各字段缺失值统计情况
print(data.isna().sum())

CRIM       0
ZN         0
INDUS      0
CHAS       0
NOX        0
RM         0
AGE        0
DIS        0
RAD        0
TAX        0
PTRATIO    0
LSTAT      0
MEDV       0
dtype: int64

 2.5.1.3 数据集划分
 将数据集划分为两份：训练集和测试集，不包括验证集。

torch.manual_seed(10)  # 随机种子

# 划分训练集和测试集
def train_test_split(X, y, train_percent=0.8):
    n = len(X)
    shuffled_indices = torch.randperm(n)  # 返回一个数值在0到n-1、随机排列的1-D Tensor
    train_set_size = int(n * train_percent)
    train_indices = shuffled_indices[:train_set_size]
    test_indices = shuffled_indices[train_set_size:]

    X = X.values
    y = y.values
    X_train = X[train_indices]
    y_train = y[train_indices]
    X_test = X[test_indices]
    y_test = y[test_indices]

    return X_train, X_test, y_train, y_test

X = data.drop(['MEDV'], axis=1)
y = data['MEDV']

X_train, X_test, y_train, y_test = train_test_split(X, y)  # X_train每一行是个样本，shape[N,D]

2.5.1.4 特征工程

为了消除纲量对数据特征之间影响，在模型训练前，需要对特征数据进行归一化处理，将数据缩放到[0, 1]区间内，使得不同特征之间具有可比性。

X_train = torch.tensor(X_train)
X_train = X_train.to(torch.float32)
X_test = torch.tensor(X_test)
X_train = X_train.to(torch.float32)
y_train = torch.tensor(y_train)
X_train = X_train.to(torch.float32)
y_test = torch.tensor(y_test)
X_train = X_train.to(torch.float32)
X_min = torch.min(X_train)
X_max = torch.max(X_train)
X_train = (X_train-X_min)/(X_max-X_min)
X_test = (X_test-X_min)/(X_max-X_min)
# 训练集构造
train_dataset = (X_train, y_train)
# 测试集构造
test_dataset = (X_test, y_test)

2.5.2 模型构建

构建一个12维的

# 模型实例化
input_size = 12
model=Linear(input_size)

2.5.3 完善Runner类

class Runner(object):
    def __init__(self, model, optimizer, loss_fn, metric):
        # 优化器和损失函数为None,不再关注
        # 模型
        self.model = model
        # 评估指标
        self.metric = metric
        # 优化器
        self.optimizer = optimizer

    def train(self, dataset, reg_lambda, model_dir):
        X, y = dataset
        self.optimizer(self.model, X, y, reg_lambda)

        # 保存模型
        self.save_model(model_dir)

    def evaluate(self, dataset, **kwargs):
        X, y = dataset

        y_pred = self.model(X)
        result = self.metric(y_pred, y)

        return result

    def predict(self, X, **kwargs):
        return self.model(X)

    def save_model(self, model_dir):
        if not os.path.exists(model_dir):
            os.makedirs(model_dir)

        params_saved_path = os.path.join(model_dir, 'params.pdtensor')
        torch.save(model.params, params_saved_path)

    def load_model(self, model_dir):
        params_saved_path = os.path.join(model_dir, 'params.pdtensor')
        self.model.params = torch.load(params_saved_path)

optimizer = optimizer_lsm
# 实例化Runner
runner = Runner(model, optimizer=optimizer, loss_fn=None, metric=mse_loss)

2.5.4 模型训练

在组装完成Runner之后，我们将开始进行模型训练、评估和测试。首先，我们先实例化Runner，然后开始进行装配训练环境，接下来就可以开始训练了，相关代码如下

# 模型保存到文件夹中
saved_dir = 'py开发'
# 启动训练
runner.train(train_dataset, reg_lambda=0, model_dir=saved_dir)

打印权重

columns_list = data.columns.to_list()
weights = runner.model.params['w'].tolist()
b = runner.model.params['b'].item()
for i in range(len(weights)):
    print(columns_list[i], "weight:", weights[i])

print("b:", b)

CRIM weight: -6.7268967628479
ZN weight: 1.28081214427948
INDUS weight: -0.4696650803089142
CHAS weight: 2.235346794128418
NOX weight: -7.0105814933776855
RM weight: 9.76220417022705
AGE weight: -0.8556219339370728
DIS weight: -9.265738487243652
RAD weight: 7.973038673400879
TAX weight: -4.365403175354004
PTRATIO weight: -7.105883598327637
LSTAT weight: -13.165120124816895
b: 32.12007522583008

从输出结果看，CRIM、PTRATIO等的权重为负数，表示该镇的人均犯罪率与房价负相关，学生与教师比例越大，房价越低。RAD和CHAS等为正，表示到径向公路的可达性指数越高，房价越高；临近Charles River房价高
2.5.5 模型测试

# 加载模型权重
runner.load_model(saved_dir)

mse = runner.evaluate(test_dataset)
print('MSE:', mse.item())

MSE: 12.345974922180176

2.5.6 模型预测

runner.load_model(saved_dir)
pred = runner.predict(X_test[:1])
print("真实房价：",y_test[:1].item())
print("预测的房价：",pred.item())

真实房价： 33.099998474121094
预测的房价： 33.04654312133789

从这个结果看来真实房价和预测房价无线接近，说明结果是正确的。

实验感想：通过这次实验对线性模型有了很深彻的感悟，以后相信遇见线性模型不会再困难。