Python机器学习日记6：线性模型（用于分类的线性模型）

一、用于分类的线性模型

线性模型也广泛应用于分类问题。

1. 二分类

二分类可以利用下面的公式进行预测：

ŷ = w[0] * x[0] + w[1] * x[1] + … + w[p] * x[p] + b > 0

这个公式看起来与线性回归的公式非常相似，但我们没有返回特征的加权求和，而是为预测设置了阈值（0）。如果函数值小于 0，我们就预测类别 -1；如果函数值大于 0，我们就预测类别 +1。对于所有用于分类的线性模型，这个预测规则都是通用的。同样，有很多种不同的方法来找出系数（w）和截距（b）。

对于用于回归的线性模型，输出 ŷ 是特征的线性函数，是直线、平面或超平面（对于更高维的数据集）。

对于用于分类的线性模型，决策边界是输入的线性函数。换句话说，（二元）线性分类器是利用直线、平面或超平面来分开两个类别的分类器。

学习线性模型有很多种算法。这些算法的区别在于以下两点：

1. 系数和截距的特定组合对训练数据拟合好坏的度量方法
2. 是否使用正则化，以及使用哪种正则化方法

不同的算法使用不同的方法来度量“对训练集拟合好坏”。由于数学上的技术原因，不可能调节 w 和 b 使得算法产生的误分类数量最少。对于我们的目的，
以及对于许多应用而言，上面第一点（称为损失函数）的选择并不重要。

最常见的两种线性分类算法是：

1. Logistic回归（logistic regression），在 linear_model.LogisticRegression中实现
2. 线性支持向量机（linear support vector machine，线性 SVM），在 svm.LinearSVC（SVC 代表支持向量分类器）中实现

注意：虽然 LogisticRegression的名字中含有回归（regression），但它是一种分类算法，并不是回归算法，不应与LinearRegression 混淆。

1.1 LogisticRegression 和 LinearSVC 模型应用到 forge 数据集

我们可以将 LogisticRegression 和 LinearSVC 模型应用到 forge 数据集上，并将线性模型找到的决策边界可视化:

from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC

X, y = mglearn.datasets.make_forge()

fig, axes = plt.subplots(1, 2, figsize=(10, 3))

for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
    clf = model.fit(X, y)
    mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5, ax=ax, alpha=.7)
    mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
    ax.set_title(clf.__class__.__name__)
    ax.set_xlabel("Feature 0")
    ax.set_ylabel("Feature 1")
axes[0].legend()

图中分别展示了 LinearSVC 和 LogisticRegression 得到的决策边界，都是直线，将顶部归为类别 1 的区域和底部归为类别 0 的区域分开了。（但都有2点误差）

换句话说，对于每个分类器而言，位于黑线上方的新数据点都会被划为类别 1，而在黑线下方的点都会被划为类别 0。

两个模型都默认使用L2 正则化（与Ridge回归一样）

mglearn.plots.plot_linear_svc_regularization()

对于 LogisticRegression 和 LinearSVC，决定正则化强度的权衡参数叫作 C。C 值越大，对应的正则化越弱。换句话说，如果参数 C 值较大，那么 LogisticRegression 和LinearSVC 将尽可能将训练集拟合到最好，而如果 C 值较小，那么模型更强调使系数向量（w）接近于 0。

较小的 C 值可以让算法尽量适应“大多数”数据点，而较大的 C 值更强调每个数据点都分类正确的重要性。下面是使用 LinearSVC 的图示:

1. 在左侧的图中，C 值很小，对应强正则化。大部分属于类别 0 的点都位于底部，大部分属于类别 1 的点都位于顶部。强正则化的模型会选择一条相对水平的线，有两个点分类错误。
2. 在中间的图中，C 值稍大，模型更关注两个分类错误的样本，使决策边界的斜率变大。
3. 在右侧的图中，C 值非常大，使得决策边界的斜率也很大，现在模型对类别 0 中所有点的分类都是正确的。类别 1 中仍有一个点分类错误，这是因为对这个数据集来说，不可能用一条直线将所有点都分类正确。右侧图中的模型尽量使所有点的分类都正确，但可能无法掌握类别的整体分布。换句话说，这个模型很可能过拟合。

与回归的情况类似，用于分类的线性模型在低维空间中看起来可能非常受限，决策边界只能是直线或平面。同样，在高维空间中，用于分类的线性模型变得非常强大，当考虑更多特征时，避免过拟合变得越来越重要。

1.2 乳腺癌数据集上详细分析 LogisticRegression

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=42)

C=1 的默认值给出了相当好的性能，在训练集和测试集上都达到 95% 的精度。但由于训练集和测试集的性能非常接近，所以模型很可能是欠拟合的。

>>> logreg = LogisticRegression().fit(X_train, y_train) # 默认C=1
>>> print("Training set score: {:.3f}".format(logreg.score(X_train, y_train)))
>>> print("Test set score: {:.3f}".format(logreg.score(X_test, y_test)))
Training set score: 0.941
Test set score: 0.965

我们尝试增大 C 来拟合一个更灵活的模型：

>>> logreg100 = LogisticRegression(C=100).fit(X_train, y_train)
>>> print("Training set score: {:.3f}".format(logreg100.score(X_train, y_train)))
>>> print("Test set score: {:.3f}".format(logreg100.score(X_test, y_test)))
Training set score: 0.951
Test set score: 0.958

使用 C=100 可以得到更高的训练集精度，也得到了稍高的测试集精度，这也证实了我们的直觉，即更复杂的模型应该性能更好。

我们还可以研究使用正则化更强的模型时会发生什么。设置 C=0.01：

>>> logreg001 = LogisticRegression(C=0.01).fit(X_train, y_train)
>>> print("Training set score: {:.3f}".format(logreg001.score(X_train, y_train)))
>>> print("Test set score: {:.3f}".format(logreg001.score(X_test, y_test)))
Training set score: 0.937
Test set score: 0.930

（数据有所不同）

正如我们所料，在图 2-1 中将已经欠拟合的模型继续向左移动，训练集和测试集的精度都比采用默认参数时更小。

最后，来看一下正则化参数 C 取三个不同的值时模型学到的系数：

在这里插入代码片

2. 多分类

许多线性分类模型只适用于二分类问题，不能轻易推广到多类别问题（除了 Logistic 回归）。将二分类算法推广到多分类算法的一种常见方法是“一对其余”（one-vs.-rest）方法。在“一对其余”方法中，对每个类别都学习一个二分类模型，将这个类别与所有其他类别尽量分开，这样就生成了与类别个数一样多的二分类模型。在测试点上运行所有二类分类器来进行预测。在对应类别上分数最高的分类器“胜出”，将这个类别标签返回作为预测结果。

每个类别都对应一个二类分类器，这样每个类别也都有一个系数（w）向量和一个截距（b）。下面给出的是分类置信方程，其结果中最大值对应的类别即为预测的类别标签：

w[0] * x[0] + w[1] * x[1] + … + w[p] * x[p] + b

多分类 Logistic 回归背后的数学与“一对其余”方法稍有不同，但它也是对每个类别都有一个系数向量和一个截距，也使用了相同的预测方法。

我们将“一对其余”方法应用在一个简单的三分类数据集上（blobs数据集
）：

from sklearn.datasets import make_blobs

X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(["Class 0", "Class 1", "Class 2"])

在这个数据集上训练一个 LinearSVC 分类器：

from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)

>>> print("Coefficient shape: ", linear_svm.coef_.shape)
>>> print("Intercept shape: ", linear_svm.intercept_.shape)
Coefficient shape:  (3, 2)
Intercept shape:  (3,)

我们看到，coef_ 的形状是 (3, 2)，说明 coef_ 每行包含三个类别之一的系数向量，每列包含某个特征（这个数据集有 2 个特征）对应的系数值。现在 intercept_ 是一维数组，保存每个类别的截距。

我们将这 3 个二类分类器给出的直线可视化:

import mglearn
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
                                  mglearn.cm3.colors):
    plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
            'Line class 2'], loc=(1.01, 0.3))

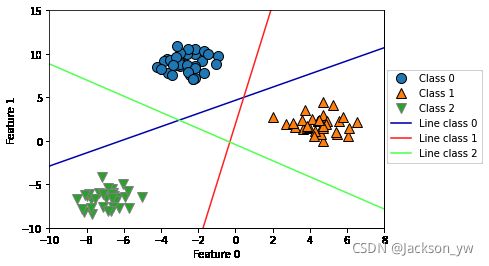
你可以看到，训练集中所有属于类别 0 的点都在与类别 0 对应的直线上方，这说明它们位于这个二类分类器属于“类别 0”的那一侧。属于类别 0 的点位于与类别 2 对应的直线上方，这说明它们被类别 2 的二类分类器划为“其余”。属于类别 0 的点位于与类别 1 对应的直线左侧，这说明类别 1 的二元分类器将它们划为“其余”。因此，这一区域的所有点都会被最终分类器划为类别 0（类别 0 的分类器的分类置信方程的结果大于 0，其他两个类别对应的结果都小于 0）。但图像中间的三角形区域属于哪一个类别呢，3 个二类分类器都将这一区域内的点划为“其余”。这里的点应该划归到哪一个类别呢？答案是分类方程结果最大的那个类别，即最接近的那条线对应的类别。

下面的例子给出了二维空间中所有区域的预测结果：

二、优缺点与参数

线性模型的主要参数是正则化参数，在回归模型中叫作 alpha，在LinearSVC 和 LogisticRegression 中叫作 C。

alpha 值较大或 C 值较小，说明模型比较简单。特别是对于回归模型而言，调节这些参数非常重要。通常在对数尺度上对 C 和 alpha 进行搜索。你还需要确定的是用 L1 正则化还是 L2 正则化。如果你假定只有几个特征是真正重要的，那么你应该用L1 正则化，否则应默认使用 L2 正则化。如果模型的可解释性很重要的话，使用 L1 也会有帮助。由于 L1 只用到几个特征，所以更容易解释哪些特征对模型是重要的，以及这些特征的作用。

线性模型的训练速度非常快，预测速度也很快。这种模型可以推广到非常大的数据集，对稀疏数据也很有效。如果你的数据包含数十万甚至上百万个样本，你可能需要研究如何使用 LogisticRegression 和 Ridge 模型的solver=‘sag’ 选项，在处理大型数据时，这一选项比默认值要更快。其他选项还有 SGDClassifier 类和 SGDRegressor 类，它们对本节介绍的线性模型实现了可扩展性更强的版本。

线性模型的另一个优点在于，利用我们之间见过的用于回归和分类的公式，理解如何进行预测是相对比较容易的。不幸的是，往往并不完全清楚系数为什么是这样的。如果你的数据集中包含高度相关的特征，这一问题尤为突出。在这种情况下，可能很难对系数做出解释。

如果特征数量大于样本数量，线性模型的表现通常都很好。它也常用于非常大的数据集，只是因为训练其他模型并不可行。但在更低维的空间中，其他模型的泛化性能可能更好。

以后会介绍几个线性模型不适用的例子。

To be continued…
欢迎继续浏览：Python机器学习日记——朴素贝叶斯分类器