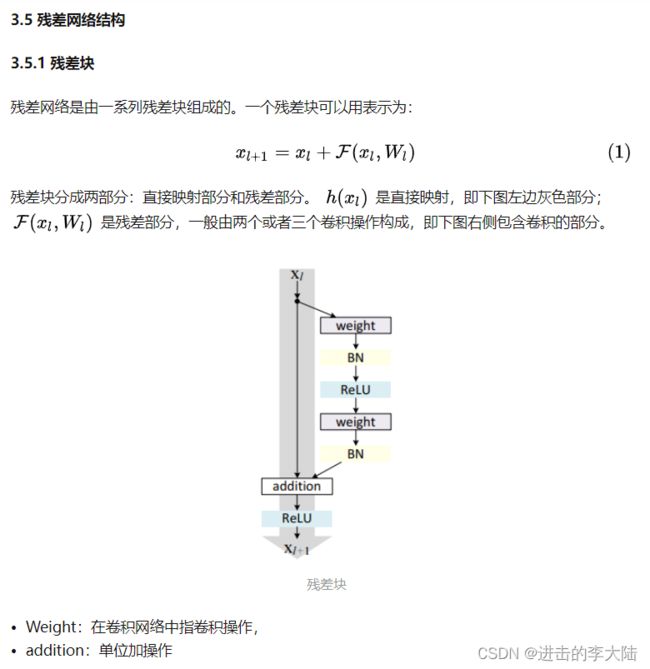
【BN、LN和梯度消失与梯度爆炸】
BN与LN
一、 为什么需要 Normalization
“独立同分布”,即independent and identically distributed,简称为 i.i.d. 独立同分布并非所有机器学习模型的必然要求(比如 Naive Bayes 模型就建立在特征彼此独立的基础之上,而Logistic Regression 和 神经网络 则在非独立的特征数据上依然可以训练出很好的模型),但独立同分布的数据可以简化常规机器学习模型的训练、提升机器学习模型的预测能力,已经是一个共识。
1) 什么是独立同分布
举一个通俗的例子:考虑掷硬币的游戏,
独立性指的是每次掷硬币的时候,前一次的结果不会影响后一次的结果。
同分布指的是每次掷硬币的时候,不管是第一次还是第1000000次,正面或反面的概率相同,也就是说概率分布是相同的。
因此,在把数据喂给机器学习模型之前,“白化(whitening)”是一个重要的数据预处理步骤。白化一般包含两个目的:(1)去除特征之间的相关性 —> 独立;(2)使得所有特征具有相同的均值和方差 —> 同分布。
2)深度神经网络模型的训练为什么会很困难?
其中一个重要的原因是,深度神经网络涉及到很多层的叠加,而每一层的参数更新会导致上层的输入数据分布发生变化,通过层层叠加,高层的输入分布变化会非常剧烈,这就使得高层需要不断去重新适应底层的参数更新。为了训好模型,我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。
二、BN算法
Batch normalization 可以被看做一个层面. 在一层层的添加神经网络的时候, 我们先有数据 X, 再添加全连接层, 全连接层的计算结果会经过 激励函数成为下一层的输入, 接着重复之前的操作. Batch Normalization (BN) 就被添加在每一个全连接和激励函数之间。
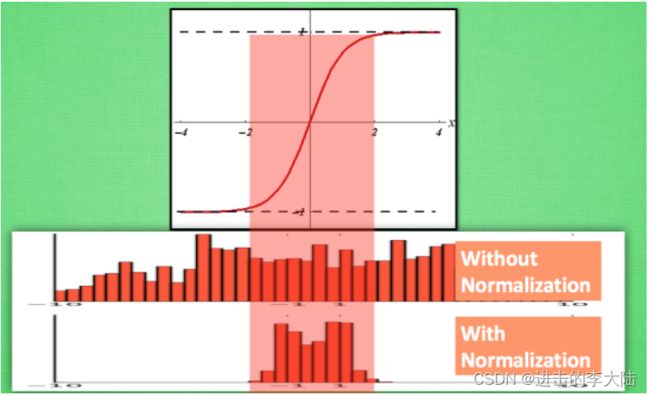
之前说过, 计算结果在进入激励函数前的值很重要, 如果我们不单单看一个值, 我们可以说, 计算结果值的分布对于激励函数很重要. 对于数据值大多分布在这个区间的数据, 才能进行更有效的传递. 对比这两个在激活之前的值的分布. 上者没有进行 normalization, 下者进行了normalization, 这样当然是下者能够更有效地利用 tanh 进行非线性化的过程。没有 normalize 的数据 使用 tanh 激活以后, 激活值大部分都分布到了饱和阶段, 也就是大部分的激活值不是-1, 就是1, 而 normalize 以后, 大部分的激活值在每个分布区间都还有存在. 再将这个激活后的分布传递到下一层神经网络进行后续计算, 每个区间都有分布的这一种对于神经网络就会更加有价值。
1)算法过程
沿着通道计算每个batch的均值u
沿着通道计算每个batch的方差σ^2
对x做归一化,x’=(x-u)/开根号(σ^2+ε)
加入缩放和平移变量γ和β ,归一化后的值,y=γx’+β
加入缩放平移变量的原因是:为了让神经网络自己去学着使用和修改这个扩展参数 gamma, 和 平移参数 β, 这样神经网络就能自己慢慢琢磨出前面的 normalization 操作到底有没有起到优化的作用, 如果没有起到作用, 我就使用 gamma 和 belt 来抵消一些。
2)BN操作举例解释
类比为一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 W 个字符。BN 求均值时,相当于把这些书按页码一一对应地加起来(例如第1本书第36页,第2本书第36页…),再除以每个页码下的字符总数:N×H×W,因此可以把 BN 看成求“平均书”的操作(注意这个“平均书”每页只有一个字),求标准差时也是同理。

3)BN的作用
1、加快网络的训练和收敛的速度
2、控制梯度爆炸防止梯度消失
3、防止过拟合
分析:
(1)加快收敛速度:在深度神经网络中中,如果每层的数据分布都不一样的话,将会导致网络非常难收敛和训练,而如果把每层的数据都在转换在均值为零,方差为1 的状态下,这样每层数据的分布都是一样的训练会比较容易收敛。通常来说,数据标准化预处理对于浅层模型就足够有效了。随着模型训练的进行,当每层中参数更新时,靠近输出层的输出较难出现剧烈变化。但对于深层神经网络来说,即使输入数据已做标准化,训练中模型参数的更新依然很容易造成靠近输出层输出的剧烈变化。这种计算数值的不稳定性通常令我们难以训练出有效的深度模型。
(2)控制梯度爆炸防止梯度消失
为了说明BN如何防止梯度消失,梯度爆炸,进而加快训练速度,举例如下:


(3)BN算法防止过拟合:在网络的训练中,BN的使用使得一个minibatch中所有样本都被关联在了一起,因此网络不会从某一个训练样本中生成确定的结果,即同样一个样本的输出不再仅仅取决于样本的本身,也取决于跟这个样本同属一个batch的其他样本,而每次网络都是随机取batch,这样就会使得整个网络不会朝这一个方向使劲学习。一定程度上避免了过拟合。
BN的缺陷:
1、高度依赖于mini-batch的大小,实际使用中会对mini-Batch大小进行约束,不适合类似在线学习(mini-batch为1)。
2、不适用于RNN网络中normalize操作:BN实际使用时需要计算并且保存某一层神经网络mini-batch的均值和方差等统计信息,对于对一个固定深度的前向神经网络(DNN,CNN)使用BN,很方便;但对于RNN来说,sequence的长度是不一致的,换句话说RNN的深度不是固定的,不同的time-step需要保存不同的statics特征,可能存在一个特殊sequence比其他的sequence长很多,这样training时,计算很麻烦。
三、LN算法
1)BN与LN的区别
LN中同层神经元输入拥有相同的均值和方差,不同的输入样本有不同的均值和方差;
BN中则针对不同神经元输入计算均值和方差,同一个batch中的输入拥有相同的均值和方差。
LN用于RNN效果比较明显,但是在CNN上,不如BN。
2)LN操作举例解释
把一个 batch 的 feature 类比为一摞书。LN 求均值时,相当于把每一本书的所有字加起来,再除以这本书的字符总数:C×H×W,即求整本书的“平均字”,求标准差时也是同理。
四、梯度消失与梯度爆炸
1)引起梯度爆炸和梯度消失的原因
2)解决方法
1.BN归一化
为了说明BN如何防止梯度消失,梯度爆炸,进而加快训练速度,举例如下:
2. 梯度剪切、正则
梯度剪切主要是针对梯度爆炸提出的,其思想是设置一个梯度剪切阈值,更新梯度时,如果梯度超过这个阈值,那么就将其强制限制在这个范围之内,防止梯度爆炸。另一种解决梯度爆炸的手段是权重正则化(weithts regularization),常见的是 l1 正则,和 l2正则。