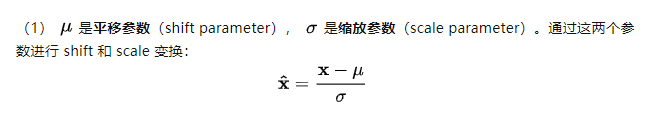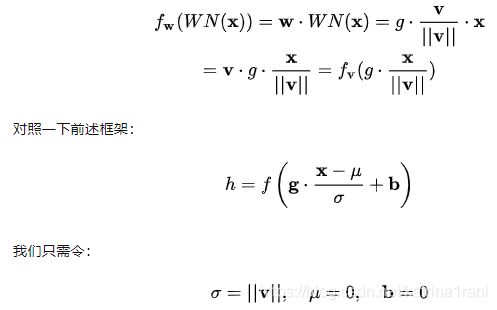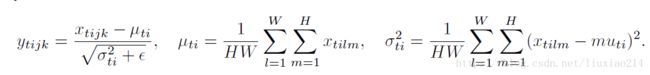深度解读BN、LN、WN、CN
一、 前言
最近有人问我 BN和LN的区别, 我开始有点懵,这两年名词儿太多,不知是啥, 一搜, Batch Normalization 和Layer Normalization, 突然就明白了一些,但是仔细一想,这两个有什么区别什么联系, 具体怎么用,我真的知道吗?虽然有的代码里也涉及到,但是从来没有细究过。
记得之前吴恩达的网易公开课也有介绍到, 例子大概是这样的,记不详细了,大概是说,样本点的分布如果是椭圆或者其它不规则形状,可能导致梯度下降的时候每个维度上的梯度下降速度不一样,且容易在较长的梯度上产生波动, Normalization可以在一定程度上缓解这个问题,使得梯度下降的方向更平缓,朝着整体梯度降低的方向学习,提高学习速度。
好了,进入正题, 以下内容参考自博客:详解深度学习中的Normalization,BN/LN/WN,并加入了我个人的理解。
二、 Normalization 原因
2.1 白化和独立同分布
机器学习界的炼丹师们最喜欢的数据有什么特点?窃以为,莫过于“独立同分布”了,即independent and identically distributed,简称为 i.i.d. 独立同分布并非所有机器学习模型的必然要求(比如 Naive Bayes 模型就建立在特征彼此独立的基础之上,而Logistic Regression 和 神经网络 则在非独立的特征数据上依然可以训练出很好的模型),但独立同分布的数据可以简化常规机器学习模型的训练、提升机器学习模型的预测能力,已经是一个共识。
因此,在把数据喂给机器学习模型之前,“白化(whitening)”是一个重要的数据预处理步骤。白化一般包含两个目的:
(1)去除特征之间的相关性 —> 独立;
(2)使得所有特征具有相同的均值和方差 —> 同分布。
白化最典型的方法就是PCA,可以参考阅读 PCAWhitening。
2.2 DL中的ICS
深度神经网络模型的训练为什么会很困难?其中一个重要的原因是,深度神经网络涉及到很多层的叠加,而每一层的参数更新会导致上层的输入数据分布发生变化,通过层层叠加,高层的输入分布变化会非常剧烈,这就使得高层需要不断去重新适应底层的参数更新。为了训好模型,我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。
Google 将这一现象总结为 Internal Covariate Shift,简称 ICS.
简而言之,每个神经元的输入数据不再是“独立同分布”。
其一,上层参数需要不断适应新的输入数据分布,降低学习速度。
其二,下层输入的变化可能趋向于变大或者变小,导致上层落入饱和区,使得学习过早停止。
其三,每层的更新都会影响到其它层,因此每层的参数更新策略需要尽可能的谨慎。
三、 Normalization 的通用框架与基本思想
深度学习中的输入:
![]()
然后通过 y = f(x) 运算后,输出一个标量值。
由于 ICS 问题的存在, x 的分布可能相差很大。要解决独立同分布的问题,“理论正确”的方法就是对每一层的数据都进行白化操作。然而标准的白化操作代价高昂,特别是我们还希望白化操作是可微的,保证白化操作可以通过反向传播来更新梯度。
可以拆成两步:
标准的公式, u是需要规范化数据的均值, ![]() 是方差。得到数据符合均值为0方差为1的标准分布。
是方差。得到数据符合均值为0方差为1的标准分布。
这里g和b是两个参数, 同深度学习中的其它参数一起训练哦~
这一步猛一看是在搞事情,仔细想下, 是为了保证模型的表达能力不因为规范化而下降。(貌似很有道理的样子,下面来解释下为什么有道理)
第一步的变换将输入数据限制到了一个全局统一的确定范围(均值为 0、方差为 1)。下层神经元可能很努力地在学习,但不论其如何变化,其输出的结果在交给上层神经元进行处理之前,将被粗暴地重新调整到这一固定范围。加入第二步不仅充分利用底层学习的能力,另一方面的重要意义在于保证获得非线性的表达能力。
再变换引入的两个新参数 g 和 b,可以表示旧参数作为输入的同一族函数,但是新参数有不同的学习动态。在旧参数中, x的均值取决于下层神经网络的复杂关联;但在新参数中,![]() 仅由b来确定,去除了与下层计算的密切耦合。新参数很容易通过梯度下降来学习,简化了神经网络的训练。
仅由b来确定,去除了与下层计算的密切耦合。新参数很容易通过梯度下降来学习,简化了神经网络的训练。
但是要说的一点是,这里只是映射到了一个确定的区间范围而已,并不是严格的独立同分布。
四、 主流Normalization方法梳理
4.1 Batch Normalization
Batch Normalization 于2015年由 Google 提出,开 Normalization 之先河。其规范化针对单个神经元进行,利用网络训练时一个 mini-batch 的数据来计算该神经元 xi 的均值和方差,因而称为 Batch Normalization。
简单直白点说,就是直接对输入的每个batch的样本进行规范化。 再具体一点, 每个batch有M个样本,每个样本特征有n个,也就是n维的输入向量,那规范化操作的其实是对向量操作,实质上是在对样本中n个维度分别去做规范化。得到的同样也是n维的规范化之后的向量。
BN理解为总想的规范化,是elment-wise的。
但是因为BN是在batch上进行的,这就要求 每一个 mini-batch 的统计量是整体统计量的近似估计,或者说每一个 mini-batch 彼此之间,以及和整体数据,都应该是近似同分布的。分布差距较小的 mini-batch 可以看做是为规范化操作和模型训练引入了噪声,可以增加模型的鲁棒性;但如果每个 mini-batch的原始分布差别很大,那么不同 mini-batch 的数据将会进行不一样的数据变换,这就增加了模型训练的难度。
BN适用场景:每个 mini-batch 比较大,数据分布比较接近。在进行训练之前,要做好充分的 shuffle.。
由于 BN 需要在运行过程中统计每个 mini-batch 的一阶统计量和二阶统计量,因此不适用于 动态的网络结构 和 RNN 网络。
说下统计量概念:
还有个地儿开始有疑问,动态网络结构,搜了下没搜到, 后来又看了看,貌似是说RNN网络做生成,需要预测下一个token的结果,输入的token维度是变化的,这样看来, BN就无法对输入batch下样本每个维度进行规范化,自然就不行了,原因看下这个吧:https://www.zhihu.com/question/308310065,其实没看太懂。。。![]()
另一点,BN不能和dropout同时使用, 因为它们对于测试集都做了特殊处理,dropout 测试的时候不需要隐藏神经元,但是需要将权重乘以 1-dropout值。(参见https://zhuanlan.zhihu.com/p/199521441), 简单来说,就是因为dropout导致实际训练中积累的均值和方差和实际测试中用到的均值和方差是存在差异的,即训练和测试的方差偏移。
4.2 Layer Normalization
简单说,接上面BN那块,就是把每个样本的x维度做规范化, 这样做的好处呢, 可以避免BN的batch太小的限制,还可以解决动态网络的限制,能适用于RNN结构,但是呢,它的问题在于,对于不同类型或者说不同区间范围的特征,不太适用。
下面来详细介绍:
与 BN 不同,LN 是一种横向的规范化,如图所示。它综合考虑一层所有维度的输入,计算该层的平均输入值和输入方差,然后用同一个规范化操作来转换各个维度的输入。
LN 针对单个训练样本进行,不依赖于其他数据,因此可以避免 BN 中受 mini-batch 数据分布影响的问题,可以用于 小mini-batch场景、动态网络场景和 RNN,特别是自然语言处理领域。此外,LN 不需要保存 mini-batch 的均值和方差,节省了额外的存储空间。
但是,BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间,而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别(比如颜色和大小),那么 LN 的处理可能会降低模型的表达能力。
4.3 Weight Normalization
前面说到f(x) = wx, 除了对x归一化之外,还可以对w进行归一化,这就是WN的由来。
但是看起来公式好像有点别扭,跟我们前面看到的规范化公式不太一样。如何对应到开始的规范化公式呢?
BN 和 LN 是用输入的特征数据的方差对输入数据进行 scale,而 WN 则是用 神经元的权重的欧氏范式对输入数据进行 scale。虽然在原始方法中分别进行的是特征数据规范化和参数的规范化,但本质上都实现了对数据的规范化,只是用于 scale 的参数来源不同。
这里的规范化只是对数据进行了 scale,而没有进行 shift,因为我们简单地令![]() =0. 但事实上,这里留下了与 BN 或者 LN 相结合的余地——那就是利用 BN 或者 LN 的方法来计算输入数据的均值
=0. 但事实上,这里留下了与 BN 或者 LN 相结合的余地——那就是利用 BN 或者 LN 的方法来计算输入数据的均值 ![]() 。
。
WN 的规范化不直接使用输入数据的统计量,因此避免了 BN 过于依赖 mini-batch 的不足,以及 LN 每层唯一转换器的限制,同时也可以用于动态网络结构。
4.4 Cosine Normalization
再看下 ![]() x和w都变换了,那我就从这个点这里来吧! 然后余弦规范化就简单粗暴的把点积变成了余弦,原理是说,点积无法限制范围,会导致数据分布的方差爆炸或消失,余弦就没有这个问题,成功将数据范围限制在了-1到1之间。但是它也有一个缺陷,那就是 点积的含义除了夹角余弦外还有向量长度信息,丢掉了部分信息可能会导致效果变差。
x和w都变换了,那我就从这个点这里来吧! 然后余弦规范化就简单粗暴的把点积变成了余弦,原理是说,点积无法限制范围,会导致数据分布的方差爆炸或消失,余弦就没有这个问题,成功将数据范围限制在了-1到1之间。但是它也有一个缺陷,那就是 点积的含义除了夹角余弦外还有向量长度信息,丢掉了部分信息可能会导致效果变差。
下面详细介绍:
我们要对数据进行规范化的原因,是数据经过神经网络的计算之后可能会变得很大,导致数据分布的方差爆炸,而这一问题的根源就是我们的计算方式——点积,权重向量w和特征数据向量x的点积。向量点积是无界(unbounded)的啊!于是 余弦规范化就出现了!
4.5 Group Normalization
Group Normalization(GN)是针对Batch Normalization(BN)在batch size较小时错误率较高而提出的改进算法,因为BN层的计算结果依赖当前batch的数据,当batch size较小时(比如2、4这样),该batch数据的均值和方差的代表性较差,因此对最后的结果影响也较大。随着batch size越来越小,BN层所计算的统计信息的可靠性越来越差,这样就容易导致最后错误率的上升;而在batch size较大时则没有明显的差别。虽然在分类算法中一般的GPU显存都能cover住较大的batch设置,但是在目标检测、分割以及视频相关的算法中,由于输入图像较大、维度多样以及算法本身原因等,batch size一般都设置比较小,所以GN对于这种类型算法的改进应该比较明显。
因此Group Normalization(GN)的思想并不复杂,简单讲就是要使归一化操作的计算不依赖batch size的大小,原文的这段话概括得非常好:GN divides the channels into groups and computes within each group the mean and variance for normalization. GN’s computation is independent of batch sizes, and its accuracy is stable in a wide range of batch sizes.
4.6 Instance Norm
BN注重对每个batch进行归一化,保证数据分布一致,因为判别模型中结果取决于数据整体分布。
但是图像风格化中,生成结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,因而对HW做归一化。可以加速模型收敛,并且保持每个图像实例之间的独立。
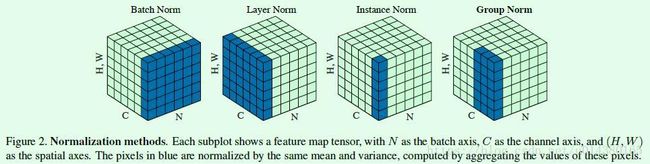
4.7 对比BN LN IN GN
Figure2是几种归一化方式的对比(Bartch Norm、Layer Norm、Instance Norm和Group Norm),可以一并回顾下BN算法。Figure2中的立方体是三维,其中两维C和N分别表示channel和batch size,第三维表示H,W,可以理解为该维度大小是H*W,也就是拉长成一维,这样总体就可以用三维图形来表示。可以看出BN的计算和batch size相关(蓝色区域为计算均值和方差的单元),而LN、BN和GN的计算和batch size无关。同时LN和IN都可以看作是GN的特殊情况(LN是group=1时候的GN,IN是group=C时候的GN)。
NLP语言解释下: N是batchsize大小, H.W 是 样本的token长度(可以理解为特征维度/神经元个数), C是通道(到NLP上,是向量维度,每个token对应的表示向量维度); 其实Batch Norm是对向量每个维度分别进行的Norm计算,理解上这么理解,但是实际上是向量操作,各个特征维度处理是同时进行的。(每个维度下一个方差均值,相当于每个batch的所有token的每一个向量维度对应一个均值方差。)BN中则针对不同神经元输入计算均值和方差,同一个batch中的输入拥有相同的均值和方差。预测的时候才用训练数据的均值方差进行。
Layer Norm:是对一层神经元进行的Norm,即对一个样本对应的所有token的向量进行Norm,(一个样本在当前层,计算得到一个均值和方差),对每一个样本的所有维度进行Norm,对应到序列模型上,也就是对一个样本的文本输入的向量所有维度进行Norm,然后需要对每一个样本都进行Norm。(LN是针对深度网络的某一层的所有神经元的输入进行normalize操作。)LN中同层神经元输入拥有相同的均值和方差,不同的输入样本有不同的均值和方差。
Instance Norm:对一个样本进行Norm,但是只对一个样本对应的token的一个向量维度进行Norm。
Group Norm:如图,计算一个样本某几个向量维度上进行Norm。
五、 Normalization有效原因
以下面这个简化的神经网络为例来分析
5.1 权重伸缩不变性
![]()
5.2 数据伸缩不变性
六、 参考文献
主要参考自上面的博客详解深度学习中的Normalization,BN/LN/WN,并参考如下链接,加入了个人思考。
RNN为什么不适合做BN?
深度学习中 Batch Normalization为什么效果好?
通俗易懂理解Batch Normalization和Layer Normalization归一化原理
BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm、SwitchableNorm总结
Group Normalization算法笔记
如有侵权,非常抱歉,请尽快联系我!