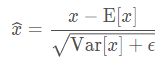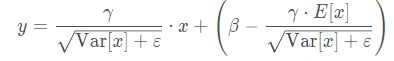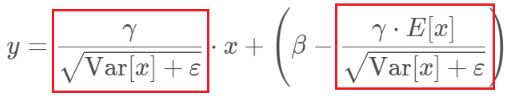Batch Normalization详解以及BN和LN的区别
前言
最近要找工作,也是复习一下面经。之前经常看过的BN也是面试中的重中之重,记得当时面试华为诺亚方舟实验室的时候,面试官就问到了我BN和LN的区别,当时也仅仅是将这两者的区别说出来了,但是并没有进行扩展,现在想想也是有点后悔的(其实当时自己也不知道该扩展啥)。在今天也就做一下总结,来概括一下这两者的区别以及BN的动机原理。
1、动机
在机器学习领域有个非常重要的假设样本之间的独立同分布,也就是训练数据和测试数据假设是满足相同分布,这样我们通过训练数据训练模型才能够在测试数据上获得较好的效果(这个独立同分布是一个前提)。 然而,往往很多时候,真实情况并不是我们希望看到的那样,也就是训练数据和测试数据往往分布会不一致,这时候往往会大大降低神经网络(其他模型也一样)的泛化能力,所以在神经网络的训练中,为了让训练数据和测试数据尽量一致,我们会对所有输入数据进行归一化处理。
那么这个和BN有啥关系呢? BN是用来解决"Internal Covariate Shift"问题的。 首先,先解释下"Covariate shift"现象, 这个指的就是训练集的数据分布和测试集的数据分布不一致。 而"internal"表示的是神经网络隐层中的数据分布不一致问题。
也就是在神经网络的训练过程中, 每个隐藏的参数都在不停的变化,从而使得后一层的输入发生变化,从而每一批训练数据的分布也会随之改变,导致了网络在每次迭代中都需要拟合不同的数据分布,这样增大了训练的复杂度以及过拟合的风险。
所以BatchNorm的基本思想就提出来了: 能不能让每个隐层节点的激活输入分布变得稳定一点呢? 作者在图像白化操作中得到了启发(所谓白化,就是对输入数据分布变换到0均值,单位方差的正态分布, 那么神经网络会较快收敛), 从而进行推论,图像是深度神经网络的输入层,做白化能加快收敛,那么其实对于深度网络来说,其中某个隐层的神经元是下一层的输入,意思是其实深度神经网络的每一个隐层都是输入层,不过是相对下一层来说而已,那么能不能对每个隐层都做白化呢?所以BN可以理解为对深层神经网络每个隐层神经元的激活值做简化版本的白化操作, 再白话一点,BN就是针对每一批数据在网络的每一层输入之前增加归一化处理(均值0,标准差为1), 这样就将所有的批数据强制在统一的分布下。
2、BN的算法流程
首先先看一下大佬翻滚的小强总结的图:
最后这句称为affine transform(仿射变换), 可以增强模型的容纳能力,使得模型自己更加灵活,让模型自己去判断是否需要去改变数据的一个分布(这里的 γ 和 β 是可学习参数, 类似于神经网络的权值w 和b ), 如果模型发现改变分布不是太好,那么让![]() 这样我们的
这样我们的![]() 依然是等于
依然是等于![]() 没有改变分布。这就是affine transform的功能,提供了一个可逆的操作, 到底需不需要改变数据分布,把这个权利交给模型自己学习。
没有改变分布。这就是affine transform的功能,提供了一个可逆的操作, 到底需不需要改变数据分布,把这个权利交给模型自己学习。
训练阶段主要是两个步骤
对于每个神经元,如果Batch为m 个样本,首先计算在当前神经元出的均值μ 和方差σ 。再对数据进行规范化,使得输入每个特征的分布均值为0,方差为1
步骤1让每一层的网络输入数据分布变得稳定,但是却导致数据表达能力的缺失,因为通过变换操作改变了原有数据的信息表达。因此,引入了参数γ (scale)和参数β (offset),再对规范化的数据进行线性变换,恢复数据本身的表达能力。如果没有这一步, 原始网络学习的特征分布会遭到破坏,还有可能失去非线性,在后面会再来分析下这个步骤的作用。
测试阶段,当一个模型训练往之后,所有参数都确定,包括均值和方差,γ 和β , 在测试的时候依然是使用公式:
由于测试的时候,是一个样本一个样本进行测试的,所以没办法求均值和方差,那么这时候可以用训练数据的。因为每次做 Mini-Batch 训练时,都会有那个 Mini-Batch 里 m 个训练实例获得的均值和方差,现在要全局统计量,只要把每个Mini-Batch的均值和方差统计量记住,然后 均值采用训练集所有 batch 均值的期望,方差采用训练集所有 batch 的方差的无偏估计即可得出全局统计量,即:
在测试时,所使用的均值和方差是整个训练集的均值和方差。整个训练集的均值和方差的值通常是在训练的同时用 移动平均法 (类似于优化器中一阶动量和二阶动量)来计算的。
所以测试的时候,总的公式如下:
这个是和训练的时候形式上一样,但是做了这种化简 可以减少计算量。因为对于每个隐层节点:
上式红框中两项都是固定值,这样两个值可以实现算好存起来,在预测的时候直接用就行了,这样比原始的公式每一步骤都现算少了除法的运算过程,当隐层节点个数多的话就有效果了。
那么之前说的, BN不是为了解决训练非常深模型的困难吗? 这东西能解决吗?这里还真的有点无心插柳柳成荫的意思, 看上面论文题目,也知道,这个算法的提出是想解决Internal Covariate Shift,来缓解过拟合的,但是由于每一层进行归一化数据分布了之后, 还捎带着缓解了梯度容易消失的问题。
3、正则化角度的BN
为什么深度神经网络随着网络深度加深,训练起来越困难,收敛越来越慢?这个在DL领域是非常好的一个问题,DL里面的很多优化方式也是针对这个问题的,各个大佬都从不同的阶段对这个问题进行了研究,比如激活函数(ReLU),优化算法,初始化策略,网络架构(跳远)等, 而BN本质上也是从某个不同的角度可以解决这个问题。
那么上面这个问题为啥会出现呢? 从BN的角度看,神经网络在做非线性变换前的激活输入值x在随着网络深度加深或者训练过程中,其分布逐渐发生偏移或者变动,所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近,所以这导致反向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。比如如果用sigmoid激活的话,我们知道,在两端的时候梯度会区域饱和(非常小)
而BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,其实就是把越来越偏的分布强制拉回比较标准的分布,这样使得激活输入值落在非线性函数对输入比较敏感的区域(梯度更大), 避免了梯度消失问题产生,当然梯度变大也意味着能加快收敛。
但是这里又会发现一个问题: 如果通过BN,把每一层的输入值都拉到了中间梯度较大的线性区域内,那么不就跟把非线性函数替换成线性函数效果相同了?我们知道,如果是多层的线性函数变换其实这个深层是没有意义的,因为多层线性网络跟一层线性网络是等价的。这意味着网络的表达能力下降了,这也意味着深度的意义就没有了。所以BN为了保证非线性的获得,对变换后的满足均值为0方差为1的x又进行了scale加上shift操作,每个神经元增加了两个参数,这两个参数是通过训练学习到的,意思是通过γ 和β 把这个值从标准正态分布左移或者右移一点并长胖一点或者变瘦一点,每个实例挪动的程度不一样,这样等价于非线性函数的值从正中心周围的线性区往非线性区动了动。核心思想应该是想找到一个线性和非线性的较好平衡点,既能享受非线性的较强表达能力的好处,又避免太靠非线性区两头使得网络收敛速度太慢。这是从线性与非线性平衡的角度又看了下上面提到的第二个步骤affine transform。
这基本上就是BN的相关知识了,下面就是BN的作用总结和缺陷,以及在卷积网络中的使用注意事项。
4、BN的用处以及和LN的对比
BN的优点:
1、改善流经网络的梯度
2、可以用更大的学习率,大幅提高训练速度:
你可以选择比较大的初始学习率,让你的训练速度飙涨。以前还需要慢慢调整学习率,甚至在网络训练到一半的时候,还需要想着学习率进一步调小的比例选择多少比较合适,现在我们可以采用初始很大的学习率,然后学习率的衰减速度也很大,因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率,也比以前的收敛速度快,因为它具有快速训练收敛的特性;
3、减少对初始化的强烈依赖, 可以不用精心设计权值初始化
4、改善正则化策略:作为正则化的一种形式,轻微减少了对dropout的需求,甚至不用dropout和L2正则。你再也不用去理会过拟合中dropout、L2正则项参数的选择问题,采用BN算法后,你可以移除这两项了参数,或者可以选择更小的L2正则约束参数了,因为BN具有提高网络泛化能力的特性;
5、再也不需要使用使用局部响应归一化层了(局部响应归一化是Alexnet网络用到的方法,搞视觉的估计比较熟悉),因为BN本身就是一个归一化网络层;
6、可以把训练数据彻底打乱(防止每批训练的时候,某一个样本都经常被挑选到,文献说这个可以提高1%的精度)。
BN的局限:
1、当batch size较小时(比如2、4这样),该batch数据的均值和方差的代表性较差,因此对最后的结果影响也较大。随着batch size越来越小,BN层所计算的统计信息的可靠性越来越差,这样就容易导致最后错误率的上升;而在batch size较大时则没有明显的差别。虽然在分类算法中一般的GPU显存都能cover住较大的batch设置,但是在目标检测、分割以及视频相关的算法中,由于输入图像较大、维度多样以及算法本身原因等,batch size一般都设置比较小,所以Group Normalization(GN)对于这种类型算法的改进应该比较明显。BN不适用当训练资源有限而无法应用较大的batch的场景。
2、由于BN训练的时候是基于一个 mini-batch 来计算均值和方差的,这相当于在梯度计算时引入噪声,如果 batchsize 很小的话, BN 就有很多不足。不适用于在线学习(batchsize = 1)
3、无法在RNN等网络中使用,因为BN不适合变长序列, 所以后来就有了Layer Normalization(LN)
4、BN在图像生成中不适用,因为图像生成里面每个样本的风格不一样,不能像BN那样多样本里面计算均值和方差,这时候需要逐个Instance(channel)计算均值方差,所以出现了Instance Normalization(IN)。
先看一张图:
![]()
相信大家看完这张图就能明白这四个归一化的区别了,也是很显而易见的。
![]()
总结
一张图做总结:
参考:重温Batch Normalization