二级倒立摆的建模、线性化S函数的PID控制以及非线性化S函数的PID控制

1 二级倒立摆的非线性建模

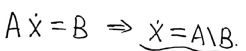
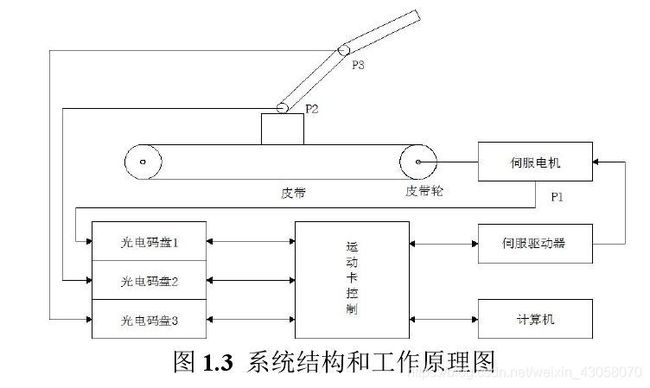首先对于下面这种二级倒立摆，对其进行建模：进行以下参数假设：可以通过参考论文，使用牛顿运动定律和拉格朗日方程，结合θ1和θ2无外力作用，列出方程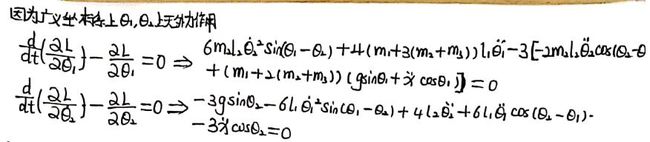：即可得到如下的对于二级倒立摆模型的非线性方程建模：

2 线性化模型、使用极点配置的PD控制

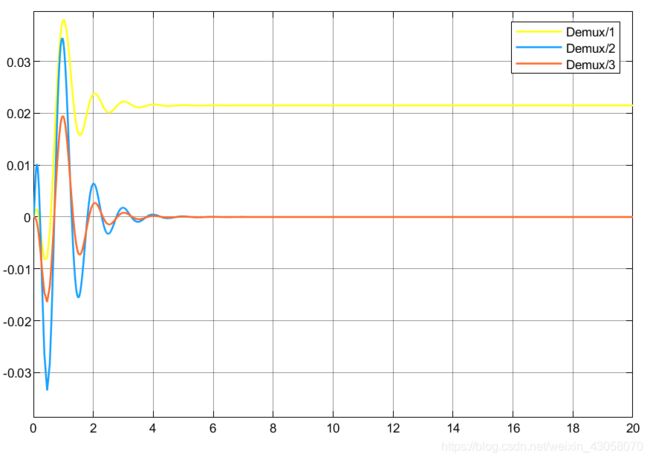
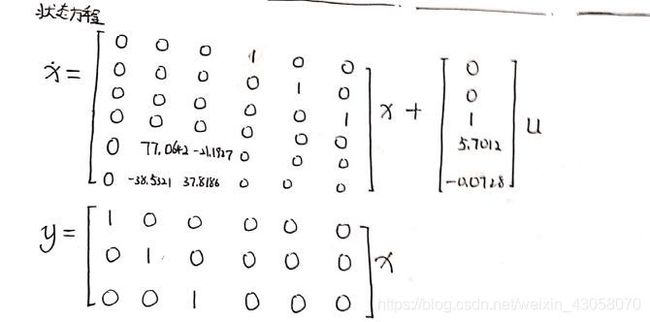通过在平衡位置进行线性化可以得到如下的状态方程：把状态方程写进S-Function函数：Inverted_Pendulum_model_linear，是一个单输入三输出，6个连续状变量态的状态方程组，即可以根据这些信息和状态方程写出S函数。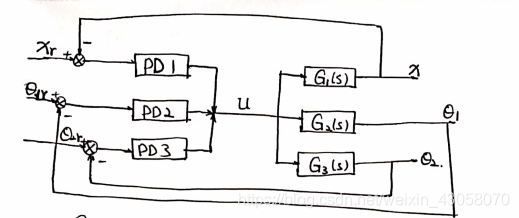
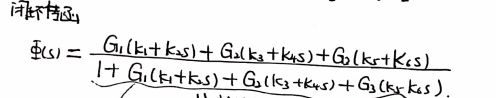
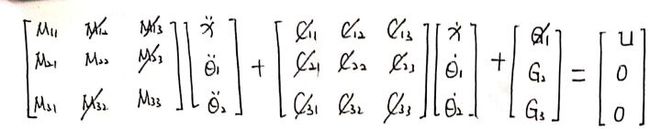分析状态方程，可以得知：二级倒立摆的线性化模型是能控，能观，但是不稳定的系统，若采用PID调节器可以使用PD，尽量避免使用I，会导致更不稳定。
若使用PD调节器，需要进行参数配置，其系统闭环控制图如下：
可以写出传递函数：

下面进行极点配置，若期望的极点是：
则令闭环传递函数的分母与其相等，解出相应的PD调节器的参数，搭建闭环系统simulink模型，进行仿真，可以得到如下的结果：

3 非线性方程建模、仿真

下面进行非线性化的建模以及仿真，非线性化是根据二级倒立摆模型的非线性方程进行变形，得到如下的形式：将非线性化方程分解得到如上的参数设计，其满足：

即可使用S-Function来得到一个单输入，三输出的非线性模型——得到Inverted_Pendulum_model_nonlinear，从而完成非线性方程S函数的建模，根据上述的线性建模匹配得到的PD调节器，进行仿真，可以得到其结果有扰动和无扰动如下：

二级倒立摆的建模、线性化S函数的PID控制以及非线性化S函数的PID控制，
(1) 根据牛顿运动定律或者拉格朗日方程，建立直线型二级倒立摆的非线性运动模型，给出系统运动的状态方程。
(2) 对非线性运动模型进行线性化，针对线性化模型采用极点配置或者PID控制的方法，设计直线型二级倒立摆的控制方案，给出控制律设计方法；
(3) 分别针对有扰动和无扰动两种情况下，采用Matlab软件进行仿真，编写倒立摆非线性运动模型的S函数，结合设计的控制方案，给出Matlab仿真的框图，并给出仿真结果。
其资源地址：https://download.csdn.net/download/weixin_43058070/11249976