心电信号去噪python

心电信号去噪python
我妥协了实话实说，比起教程，这篇算是一个笔记吧，在我做心电的过程中，观察了一下心电相关的去噪方法，国内主要集中在应用中值滤波和小波变换，国外一般直接用一巴特沃斯了事。目前我只会应用，本来我是想理论都吃透了再写的，奈何类似小波之类的基本原理学起来实在一言难尽，说白了还是能力不够 ，等我再学一遍数字信号处理归来之日就是将理论补足之时。

---

1.巴特沃斯滤波器

1.1 巴特沃斯高通滤波

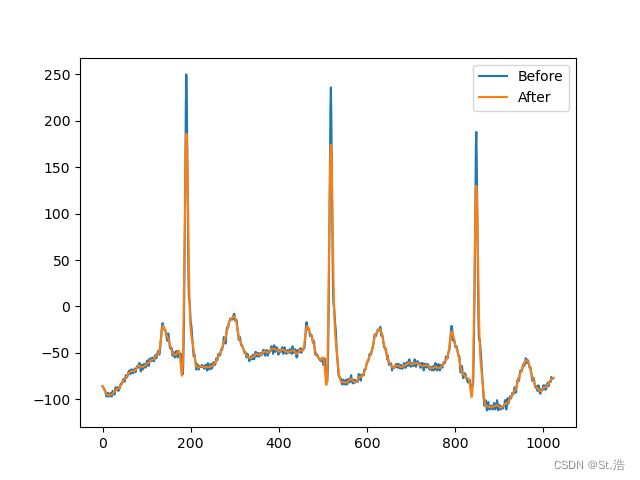
巴特沃斯滤波器是心电信号滤波最好用的滤波器，一个低频的高通滤波器可以去除基线漂移
比起我之前写了一整篇中值滤波，虽然巴特沃斯手搓不出来但是确实好用多了

import matplotlib.pyplot as plt
import pywt
from scipy import signal

#Frequence 为信号的采样频率
#lowpass 高通滤波器可以通过的最低频率

def high_fliter(data, frequency=256, lowpass=1):
	#3是滤波器阶数 
	#lowpass / frequency * 2 计算机截至频率
	#[b, a]为设计好的滤波器的系统函数的系数
    [b, a] = signal.butter(3, lowpass / frequency * 2, 'highpass')
	# 将设计好的系数和待滤波的信号扔进filtfilt中返回值为滤波之后的结果
    Signal_pro = signal.filtfilt(b, a, data)
    return Signal_pro

ecg = pywt.data.ecg() # 生成心电信号
fliter_ecg = high_fliter(ecg)#滤波

#画图
plt.plot(ecg)
plt.plot(fliter_ecg)
plt.legend(['Before','After'])
plt.show()

1.2巴特沃斯低通滤波

巴特沃斯的低通滤波还可以用于去除工频干扰，也就是去除信号的高频部分，让信号变得平滑

import matplotlib.pyplot as plt
import pywt
from scipy import signal

#Frequence 为信号的采样频率
#highpass 低通滤波器可以通过的最高频率

def loss_fliter(data, frequency=256, highpass=20):
    [b, a] = signal.butter(3, highpass / frequency * 2, 'lowpass')
    Signal_pro = signal.filtfilt(b, a, data)
    return Signal_pro

ecg = pywt.data.ecg() # 生成心电信号
fliter_ecg = loss_fliter(ecg)#滤波

#画图
plt.plot(ecg)
plt.plot(fliter_ecg)
plt.legend(['Before','After'])
plt.show()

1.3巴特沃斯带通滤波

好了大朋友们（幼儿园式提问）
怎么把工频干扰（高频噪声）和基线漂移（低频噪声）同时滤掉呢？
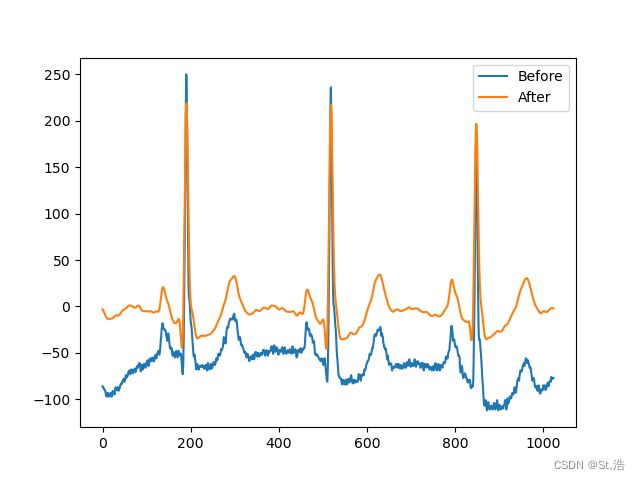
dada~ 那就是带通滤波了！
就是这吗简单我们得到了又简单又板正的心电信号

import matplotlib.pyplot as plt
import pywt
from scipy import signal

#Frequence 为信号的采样频率
#highpass 低通滤波器可以通过的最高频率
#lowpass  高通滤波器可以通过的最低频率

def singnal_fliter(data, frequency=256, highpass=20, lowpass=1):
    [b, a] = signal.butter(3, [lowpass / frequency * 2, highpass / frequency * 2], 'bandpass')
    Signal_pro = signal.filtfilt(b, a, data)
    return Signal_pro

ecg = pywt.data.ecg() # 生成心电信号
fliter_ecg = singnal_fliter(ecg)#滤波

#画图
plt.plot(ecg)
plt.plot(fliter_ecg)
plt.legend(['Before','After'])
plt.show()

2.小波分解

ok whatever 上面的巴特沃斯基本上就能解决问题，用小波其实也没什么大的必要，可能大多数人只是看论文的时候发现，好像大家都在用，是不是就得用，其实不是，你会发现，所有的论文里都没有滤波方法选用小波和选用其他方法的对比。根据我自己的实验也没什么提升，全是趋炎附势的用。如果为了毕设凑内容以后也不从事科研，用就用了，要是做科研的话这一部分应该自己辩证性的思考一下，接下来进入正题。

小波分解，抛去复杂的理论，最终呈现的效果就是一个信号的多种频率进行分析，得到不同的频率分量，就是原信号中不同频率的信号

import matplotlib.pyplot as plt
import pywt
import numpy as np
ecg = pywt.data.ecg() # 生成心电信号

w = pywt.Wavelet('db8') # 选用Daubechies8小波

#获取小波分解的最大层级
maxlev = pywt.dwt_max_level(len(ecg), w.dec_len)
coeffs = pywt.wavedec(ecg,'db8', level=maxlev) # 将信号进行小波分解
datarec = pywt.waverec(coeffs, 'db8') # 将信号进行小波重构

datarec1 = pywt.waverec(np.multiply(coeffs,[1, 0, 0, 0, 0, 0, 0]).tolist(), 'db8') # 将信号进行小波重构
datarec2 = pywt.waverec(np.multiply(coeffs,[0, 1, 0, 0, 0, 0, 0]).tolist(), 'db8') # 将信号进行小波重构
datarec3 = pywt.waverec(np.multiply(coeffs,[0, 0, 1, 0, 0, 0, 0]).tolist(), 'db8') # 将信号进行小波重构
datarec4 = pywt.waverec(np.multiply(coeffs,[0, 0, 0, 1, 0, 0, 0]).tolist(), 'db8') # 将信号进行小波重构
datarec5 = pywt.waverec(np.multiply(coeffs,[0, 0, 0, 0, 1, 0, 0]).tolist(), 'db8') # 将信号进行小波重构
datarec6 = pywt.waverec(np.multiply(coeffs,[0, 0, 0, 0, 0, 1, 0]).tolist(), 'db8') # 将信号进行小波重构
datarec7 = pywt.waverec(np.multiply(coeffs,[0, 0, 0, 0, 0, 0, 1]).tolist(), 'db8') # 将信号进行小波重构

plt.subplot(8, 1, 1)
plt.plot(datarec1)
plt.subplot(8, 1, 2)
plt.plot(datarec2)
plt.subplot(8, 1, 3)
plt.plot(datarec3)
plt.subplot(8, 1, 4)
plt.plot(datarec4)
plt.subplot(8, 1, 5)
plt.plot(datarec5)
plt.subplot(8, 1, 6)
plt.plot(datarec6)
plt.subplot(8, 1, 7)
plt.plot(datarec7)
plt.subplot(8, 1, 8)
plt.plot(datarec)

plt.show()

小波波分解重构的过程
1.选择小波
2.分解得到小波层系数coeffs
3.用小波和coeffs重构回去
已知小波类型和被分解信号的长度之后，信号最大的分解层数就是确定的
从上面分解的结果图就能看出除了最后一个信号也就是原信号外
对应了7个分量的信号
肉眼可见加上毕生所学也能看出来频率从低到高的

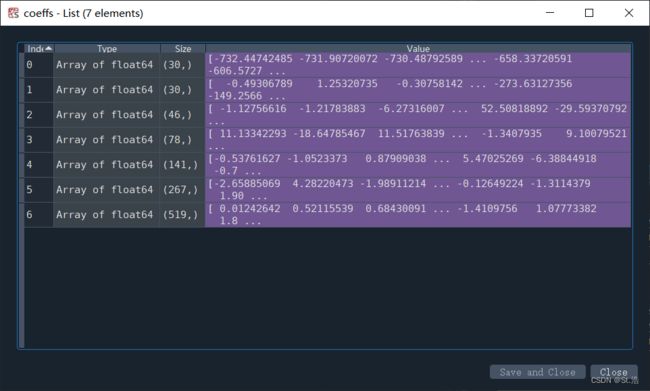
小波的分解也好滤波也好就是改变重构用到的coeffs对应分量的系数，对这些暗地里动一动手脚，重构回去之后信号发现自己哪里好像变了，这时候这个信号就不知不觉被我们绿了，哦不，滤了。
小波分解通过将其他层的参数都变成0再进行重构得到对应层的小波分量信号。

如果想的到指定的对应分量信号的组合

import pywt
import numpy as np
import matplotlib.pyplot as plt

ecg = pywt.data.ecg() # 生成心电信号
w = pywt.Wavelet('db8') # 选用Daubechies8小波
maxlev = pywt.dwt_max_level(len(ecg), w.dec_len)
coeffs = pywt.wavedec(ecg,'db8', level=maxlev) # 将信号进行小波分解

#乘积因子全置1 重构的datarec与原信号相同
datarec = pywt.waverec(np.multiply(coeffs,[1, 1, 1, 1, 1, 1, 1]).tolist(), 'db8') # 将信号进行小波重构

#将最高频和最低频的分量的乘积因子置0再重构得到去除最高频分量和最低频分量的信号
datarec1 = pywt.waverec(np.multiply(coeffs,[0, 1, 1, 1, 1, 1, 0]).tolist(), 'db8') # 将信号进行小波重构

plt.subplot(311)
plt.plot(ecg)
plt.subplot(312)
plt.plot(datarec)
plt.subplot(313)
plt.plot(ecg)
plt.plot(datarec1)
plt.legend(['before','After'])
plt.show()

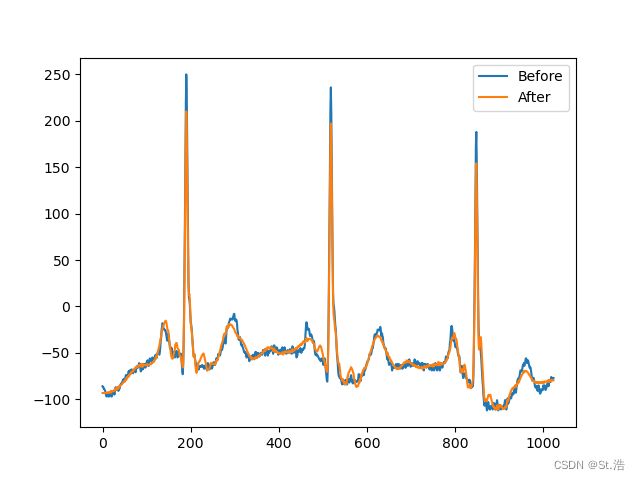
3.小波滤波

不像小波分解那样大改参数，每一层的系数都稍微改一点然后再重构回去就能得到下面的效果

import pywt
import matplotlib.pyplot as plt

ecg = pywt.data.ecg() # 生成心电信号
w = pywt.Wavelet('db8') # 选用Daubechies8小波

maxlev = pywt.dwt_max_level(len(ecg), w.dec_len)
threshold = 0.1 # Threshold for filtering

coeffs = pywt.wavedec(ecg,'db8', level=maxlev) # 将信号进行小波分解

#这里就是对每一层的coffe进行更改
for i in range(1, len(coeffs)):
    coeffs[i] = pywt.threshold(coeffs[i], threshold*max(coeffs[i])) 


datarec = pywt.waverec(coeffs, 'db8') # 将信号进行小波重构

plt.plot(ecg)
plt.plot(datarec)
plt.legend(['Before','After'])
plt.show()

第二种在skimage.restoration库中还有denoise_wavelet函数可以直接滤波
这个代码来自于B站的一位叫周大宝永远不秃的up主搬运的国外的一位老师的小波变换的应用视频中的一个例子。

import numpy as np
import pywt
from skimage.restoration import denoise_wavelet
import matplotlib.pyplot as plt

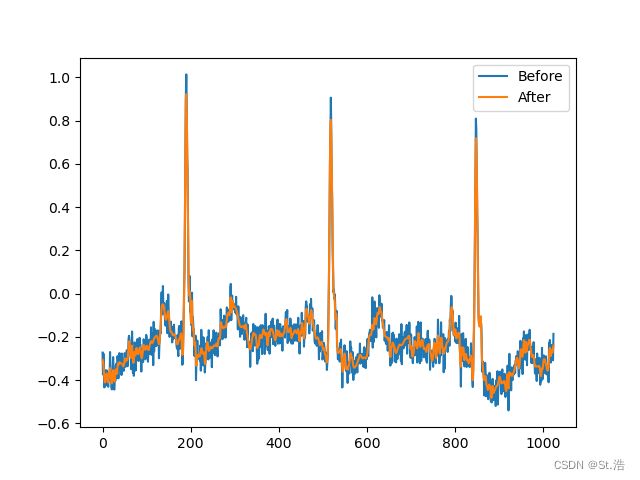
ecg = pywt.data.ecg().astype(float) / 256

w = pywt.Wavelet('db8') # 选用Daubechies8小波

sigma = 0.05
#给信号加上高斯噪声
ecg_noisy = ecg + sigma * np.random.randn(ecg.size)
maxlev = pywt.dwt_max_level(len(ecg), w.dec_len)

ecg_denoise = denoise_wavelet(ecg_noisy, method='BayesShrink', mode='soft', wavelet_levels=maxlev, wavelet='db8')

plt.plot(ecg_noisy)
plt.plot(ecg_denoise)
plt.legend(['Before','After'])
plt.show()

3.中值滤波

额，嘿嘿因为之前写过了就直接挂了链接，想了解中值波的请过目下面的愚作
链接: 超入门级-基于中值滤波处理ECG信号的基线漂移-Python-MIT-BIH数据集

总结

没办法不能像之前一样从原理非常详细的分析，因为还没有对内容比较通透理解，只能从一个工科生的角度从自己所了解的应用入手，所以这个可能比较偏笔记性质，有一些函数需要自己去稍微查一查，接下来除非我有朝一日自己重学数字信号处理归来，不然应该就不会写心电信号处理部分的内容了，应该是一维信号的深度学习模型了，再见。