MATLAB 轮式机器人轨迹跟踪仿真
两轮式移动机器人参考点位于机器人驱动轴中心模型分析:
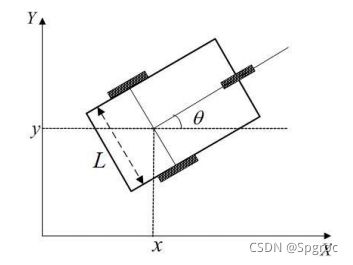
控制目标是使机器人在二维平面中运动到指定位置,但由于轮式机器人不能进行平移运动,故其状态变量不能只取(x,y),应考虑车头朝向问题,所以小车的状态变量用向量表示为:
q = [ x , y , θ ] T q=[x, y, \theta]^{T} q=[x,y,θ]T
(x,y)为机器人当前位置,theta为机器人的车头方向,机器人只能沿着垂直与驱动轴的方向移动,故移动机器人的运动约束为:
x ˙ sin θ − y ˙ cos θ = 0 \dot{x} \sin \theta-\dot{y} \cos \theta=0 x˙sinθ−y˙cosθ=0
将机器人驱动轴方向的运动力抵消掉
在这个约束条件下,移动机器人的运动学模型可以用
x ˙ = v cos θ y ˙ = v sin θ θ ˙ = ω \dot{x}=v \cos \theta \quad \dot{y}=v \sin \theta \quad \dot{\theta}=\omega x˙=vcosθy˙=vsinθθ˙=ω
其中,v和omega分别表示移动机器人的线性速度和角速度
假设参考轨迹是可行的,并由以下虚拟机器人生成
x ˙ d = v d cos θ d y ˙ d = v d sin θ d θ ˙ d = ω d \dot{x}_{d}=v_{d} \cos \theta_{d} \quad \dot{y}_{d}=v_{d} \sin \theta_{d} \quad \dot{\theta}_{d}=\omega_{d} x˙d=vdcosθdy˙d=vdsinθdθ˙d=ωd
q d = [ x d , y d , θ d ] T q_{d}=\left[x_{d}, y_{d}, \theta_{d}\right]^{T} qd=[xd,yd,θd]T
那么我们的控制目标是为移动机器人设计一个连续反馈控制律(v,ω),同时解决稳定和跟踪问题,控制目标为:
lim t → ∞ ( q ( t ) − q d ( t ) ) = 0 \lim _{t \rightarrow \infty}\left(q(t)-q_{d}(t)\right)=0 t→∞lim(q(t)−qd(t))=0
参考文献:
Simultaneous Stabilization and Tracking of Nonholonomic Mobile Robots: A Lyapunov-Based Approach
两轮式移动机器人参考点位于机器人驱动轴中心前偏离L模型分析:

机器人的状态变量用向量表示为:
x = [ x , y , θ ] T x=[x, y, \theta]^{T} x=[x,y,θ]T
图中对于xp点有
x p = [ x , y ] ⊤ \mathbf{x}_{p}=\left[\begin{array}{ll} x, y \end{array}\right]^{\top} xp=[x,y]⊤
对于偏移点S(x)有
s ( x ) = x p + l [ cos ( θ ) sin ( θ ) ] s(\mathbf{x})=\mathbf{x}_{p}+l\left[\begin{array}{c} \cos (\theta) \\ \sin (\theta) \end{array}\right] s(x)=xp+l[cos(θ)sin(θ)]
这样S(x)点的运动将没有约束条件,机器人的运动学模型为:
x ˙ = [ cos ( θ ) 0 sin ( θ ) 0 0 1 ] [ v ω ] \dot{\mathbf{x}}=\left[\begin{array}{cc} \cos (\theta) & 0 \\ \sin (\theta) & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} v \\ \omega \end{array}\right] x˙=⎣⎡cos(θ)sin(θ)0001⎦⎤[vω]
s(x)的导数为:
s ˙ ( x ) = x ˙ p + l θ ˙ [ − sin ( θ ) cos ( θ ) ] \dot{s}(\mathbf{x})=\dot{\mathbf{x}}_{p}+l\dot{\theta}\left[\begin{array}{c} -\sin (\theta) \\ \cos (\theta) \end{array}\right] s˙(x)=x˙p+lθ˙[−sin(θ)cos(θ)]
得到:
s ˙ ( x ) = R l ( θ ) [ v ω ] \dot{s}(\mathbf{x})=R_{l}(\theta)\left[\begin{array}{l} v \\ \omega \end{array}\right] s˙(x)=Rl(θ)[vω]
其中
R l ( θ ) = [ cos ( θ ) − l sin ( θ ) sin ( θ ) l cos ( θ ) ] R_{l}(\theta)=\left[\begin{array}{cc} \cos (\theta) & -l\sin (\theta) \\ \sin (\theta) & l \cos (\theta) \end{array}\right] Rl(θ)=[cos(θ)sin(θ)−lsin(θ)lcos(θ)]
R l − 1 ( θ ) = [ cos ( θ ) sin ( θ ) − 1 l sin ( θ ) 1 l cos ( θ ) ] R_{l}^{-1}(\theta)=\left[\begin{array}{cc} \cos (\theta) & \sin (\theta) \\ -\frac{1}{l} \sin (\theta) & \frac{1}{l} \cos (\theta) \end{array}\right] Rl−1(θ)=[cos(θ)−l1sin(θ)sin(θ)l1cos(θ)]
最终有:
[ v ω ] = R l − 1 ( θ ) s ˙ ( x ) \left[\begin{array}{c} v \\ \omega \end{array}\right]=R_{l}^{-1}(\theta) \dot{s}(\mathbf{x}) [vω]=Rl−1(θ)s˙(x)
这样就可以根据 s ˙ ( x ) \dot{s}(\mathbf{x}) s˙(x)求出机器人的线速度与角速度,进而对机器人进行控制
参考文献:
The Robotarium: Globally Impactful Opportunities, Challenges, and Lessons Learned in Remote-Access, Distributed Control of Multirobot Systems
MATLAB仿真
根据上述关系,我们最终要输出的为机器人的线速度与角速度,进而控制机器人跟踪期望轨迹,假定期望位置为
x r , y r {x}_{r} ,{y}_{r} xr,yr
在x,y, θ \theta θ方向上的误差分别为:
e x = x r − x , e y = y r − y , e θ = θ r − θ {e}_{x}={x}_{r}-x,{e}_{y}={y}_{r} -{y},{e}_{\theta}={\theta}_{r} -{\theta} ex=xr−x,ey=yr−y,eθ=θr−θ
定义位姿跟踪误差:
q e = [ x e y e θ e ] = [ cos θ sin θ 0 − sin θ cos θ 0 0 0 1 ] [ x r − x y r − y θ r − θ ] q_{e}=\left[\begin{array}{c} x_{e} \\ y_{e} \\ \theta_{e} \end{array}\right]=\left[\begin{array}{ccc} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x_{r}-x \\ y_{r}-y \\ \theta_{r}-\theta \end{array}\right] qe=⎣⎡xeyeθe⎦⎤=⎣⎡cosθ−sinθ0sinθcosθ0001⎦⎤⎣⎡xr−xyr−yθr−θ⎦⎤
求导得到:
x ˙ e = − θ ˙ sin θ ( x r − x ) + cos θ ( x ˙ r − x ˙ ) + θ ˙ cos θ ( y r − y ) + sin θ ( y ˙ r − y ˙ ) = θ ˙ [ − sin θ ( x r − x ) + cos θ ( y r − y ) ] − v + ν r ( cos θ r cos θ + sin θ r sin θ ) = ω y e − v + v r cos θ e \begin{aligned} \dot{x}_{e} &=-\dot{\theta} \sin \theta\left(x_{r}-x\right)+\cos \theta\left(\dot{x}_{r}-\dot{x}\right)+\dot{\theta} \cos \theta\left(y_{r}-y\right)+\sin \theta\left(\dot{y}_{r}-\dot{y}\right) \\ &=\dot{\theta}\left[-\sin \theta\left(x_{r}-x\right)+\cos \theta\left(y_{r}-y\right)\right]-v+\nu_{r}\left(\cos \theta_{r} \cos \theta+\sin \theta_{r} \sin \theta\right) \\ &=\omega y_{e}-v+v_{r} \cos \theta_{e} \end{aligned} x˙e=−θ˙sinθ(xr−x)+cosθ(x˙r−x˙)+θ˙cosθ(yr−y)+sinθ(y˙r−y˙)=θ˙[−sinθ(xr−x)+cosθ(yr−y)]−v+νr(cosθrcosθ+sinθrsinθ)=ωye−v+vrcosθe
y ˙ e = − θ ˙ cos θ ( x r − x ) − sin θ ( x ˙ r − x ˙ ) − θ ˙ sin θ ( y r − y ) + cos θ ( y ˙ r − y ˙ ) = − θ ˙ [ cos θ ( x r − x ) + sin θ ( y r − y ) ] + ν r ( − cos θ r sin θ + sin θ r cos θ ) = − ω x e + v r sin θ e \begin{aligned} \dot{y}_{e} &=-\dot{\theta} \cos \theta\left(x_{r}-x\right)-\sin \theta\left(\dot{x}_{r}-\dot{x}\right)-\dot{\theta} \sin \theta\left(y_{r}-y\right)+\cos \theta\left(\dot{y}_{r}-\dot{y}\right) \\ &=-\dot{\theta}\left[\cos \theta\left(x_{r}-x\right)+\sin \theta\left(y_{r}-y\right)\right]+\nu_{r}\left(-\cos \theta_{r} \sin \theta+\sin \theta_{r} \cos \theta\right) \\ &=-\omega x_{e}+v_{r} \sin \theta_{e} \end{aligned} y˙e=−θ˙cosθ(xr−x)−sinθ(x˙r−x˙)−θ˙sinθ(yr−y)+cosθ(y˙r−y˙)=−θ˙[cosθ(xr−x)+sinθ(yr−y)]+νr(−cosθrsinθ+sinθrcosθ)=−ωxe+vrsinθe
整理位姿误差微分方程为:
[ x ˙ e y ˙ e θ ˙ e ] = [ ω y e − v + v r cos θ e − ω x e + v r sin θ e ω r − ω ] \left[\begin{array}{c} \dot{x}_{e} \\ \dot{y}_{e} \\ \dot{\theta}_{e} \end{array}\right]=\left[\begin{array}{c} \omega y_{e}-v+v_{r} \cos \theta_{e} \\ -\omega x_{e}+v_{r} \sin \theta_{e} \\ \omega_{r}-\omega \end{array}\right] ⎣⎡x˙ey˙eθ˙e⎦⎤=⎣⎡ωye−v+vrcosθe−ωxe+vrsinθeωr−ω⎦⎤
根据上述得到的运动学方程,自主导航车轨迹跟踪的问题转化为设计输入控制量 q = ( v w ) T q=\left(\begin{array}{ll}v & w\end{array}\right)^{T} q=(vw)T使闭环系统位姿误差 p e {p}_{e} pe凡能够全局一致有界,并且当 t → ∞ t \rightarrow \infty t→∞,系统在任意的初始跟踪误差下有 lim t → ∞ [ ∣ x e ( t ) ∣ + ∣ y e ( t ) ∣ + ∣ θ e ( t ) ∣ ] = 0 \lim _{t \rightarrow \infty}\left[\left|x_{e}(t)\right|+\left|y_{e}(t)\right|+\left|\theta_{e}(t)\right|\right]=0 limt→∞[∣xe(t)∣+∣ye(t)∣+∣θe(t)∣]=0。
根据自主导航车的位姿误差微分方程,可以选取函数如下:
V = k 1 2 ( x e 2 + y e 2 ) + 2 ( sin θ e 2 ) 2 ≥ 0 \mathrm{V}=\frac{k_{1}}{2}\left(x_{e}^{2}+y_{e}^{2}\right)+2\left(\sin \frac{\theta_{e}}{2}\right)^{2} \geq 0 V=2k1(xe2+ye2)+2(sin2θe)2≥0
将其微分得:
V ˙ = k 1 ( x e x ˙ e + y e y ˙ e ) + 2 sin θ e 2 cos θ e e θ ˙ e = k 1 [ x e ( v r cos θ e − v + y e ω ) + y e ( v r sin θ e − x e ω ) ] + ( ω r − ω ) sin θ e = k 1 [ x e v r cos θ e − v x e ] + k 1 y c v r sin θ e + ( ω r − ω ) sin θ e \begin{aligned} \dot{\mathrm{V}} &=k_{1}\left(x_{e} \dot{x}_{e}+y_{e} \dot{y}_{e}\right)+2 \sin \frac{\theta_{e}}{2} \cos \frac{\theta_{e}}{e} \dot{\theta}_{e} \\ &=k_{1}\left[x_{e}\left(v_{r} \cos \theta_{e}-v+y_{e} \omega\right)+y_{e}\left(v_{r} \sin \theta_{e}-x_{e} \omega\right)\right]+\left(\omega_{r}-\omega\right) \sin \theta_{e} \\ &=k_{1}\left[x_{e} v_{r} \cos \theta_{e}-v x_{e}\right]+k_{1} y_{c} v_{r} \sin \theta_{e}+\left(\omega_{r}-\omega\right) \sin \theta_{e} \end{aligned} V˙=k1(xex˙e+yey˙e)+2sin2θecoseθeθ˙e=k1[xe(vrcosθe−v+yeω)+ye(vrsinθe−xeω)]+(ωr−ω)sinθe=k1[xevrcosθe−vxe]+k1ycvrsinθe+(ωr−ω)sinθe
由此可得控制律为:
q = [ v w ] = [ v r cos θ e + k 2 x e w r + k 1 v r y e + k 3 sin θ e ] q=\left[\begin{array}{c} v \\ w \end{array}\right]=\left[\begin{array}{c} v_{r} \cos \theta_{e}+k_{2} x_{e} \\ w_{r}+k_{1} v_{r} y_{e}+k_{3} \sin \theta_{e} \end{array}\right] q=[vw]=[vrcosθe+k2xewr+k1vrye+k3sinθe]
其中,控制参数 k 2 , k 3 > 0 k_{2}, k_{3}>0 k2,k3>0。
(上述控制律的实验效果并不好,可能是参数数值选取的不恰当,可自行尝试,下面进行单纯比例控制实验)
单纯比例控制:
我们的目标是跟踪误差为0,即 e x , e y {e}_{x},{e}_{y} ex,ey为0
我们设
e ˙ x = − K e x , e ˙ y = − K e y \dot{e}_{x}=-K{e}_{x},\dot{e}_{y}=-K{e}_{y} e˙x=−Kex,e˙y=−Key
这个系统的平衡点就为(0,0),相当对进行了比例控制,而针对有偏移参考点,可将模型看成一阶积分器,这样可将输入描述为:
x ˙ = u x , y ˙ = u y \dot{x}={u}_{x}, \dot{y}={u}_{y} x˙=ux,y˙=uy
下面进行编程实现:
1,求出期望位置与当前位置的偏差
2,将偏差输入到控制器,根据变换关系 [ v ω ] = R l − 1 ( θ ) s ˙ ( x ) \left[\begin{array}{c}v \\\omega\end{array}\right]=R_{l}^{-1}(\theta) \dot{s}(\mathbf{x}) [vω]=Rl−1(θ)s˙(x)求出线速度与角速度
3,跟据 x = x + δ x , y = y + δ y , θ = θ + δ θ , {x}={x}+\delta x,{y}={y}+\delta y,{\theta}={\theta}+\delta \theta, x=x+δx,y=y+δy,θ=θ+δθ,求出下一时刻的位置及车头朝向
4,进行循环求解跟踪
跟踪效果如下:

附代码:
clear all;clc;
%% define constant
l=0.2;
R=1;
K=0.1;
delta_T=0.5;
%% define initialization
Pos=[0,12,3/2*pi]; %X,Y,Theta
T=linspace(0,2*pi,200);
desire_Pos=[16*power(sin(T),3);13*cos(T)-5*cos(2*T)-2*cos(3*T)-cos(4*T)];
%% Graphics
f3=figure;
xlabel('x (m)')
ylabel('y (m)')
grid on
%% robot dimensions
A.R_w = 1/2; % robot width/2
A.R_l= 2/2; % robot length/2
A.a1 = [-A.R_l -A.R_w]';
A.b1 = [A.R_l -A.R_w/2]';
A.b2 = [A.R_l A.R_w/2]';
A.c = [-A.R_l A.R_w]';
A.P = [A.a1 A.b1 A.b2 A.c];
A.Rot = [ cos(Pos(3)) -sin(Pos(3)); sin(Pos(3)) cos(Pos(3))]*A.P; %rotated car
A.Prot_trasl = A.Rot + [ ones(1,4)*Pos(1); ones(1,4)*Pos(2)]; % add offset of car's center
A.P_robot=patch(A.P(1,:),A.P(2,:),'b');
A.P_robot.XData=A.Prot_trasl(1,:)';
A.P_robot.YData=A.Prot_trasl(2,:)';
%% define controller
%% draw picture
h= animatedline('color','r','LineStyle','--');
h_car= animatedline('color','b');
h_car_model = animatedline('Marker','o','MaximumNumPoints',1); %只显示1个新的点
axis([-20 20 -20 15])
for k = 1:length(T)
addpoints(h_car,Pos(1),Pos(2));
addpoints(h_car_model,Pos(1),Pos(2));
e_x=Pos(1)-desire_Pos(1,k);
e_y=Pos(2)-desire_Pos(2,k);
u_x=-K*e_x;
u_y=-K*e_y;
A_mat=[cos(Pos(3)) -l*sin(Pos(3));sin(Pos(3)) l*cos(Pos(3))];
P=[cos(Pos(3)) 0;sin(Pos(3)) 0;0 1];
U_mat=[u_x,u_y]';
v_w_mat=A_mat\U_mat;
Pos(1)=Pos(1)+v_w_mat(1)*cos(Pos(3))-v_w_mat(2)*l*sin(Pos(3));
Pos(2)=Pos(2)+v_w_mat(1)*sin(Pos(3))+v_w_mat(2)*l*cos(Pos(3));
Pos(3)=Pos(3)+v_w_mat(2)*delta_T;
addpoints(h,desire_Pos(1,k),desire_Pos(2,k));
A.Rot = [cos(Pos(3)) -sin(Pos(3)); sin(Pos(3)) cos(Pos(3))]*A.P; %rotated car
A.Prot_trasl = A.Rot + [ones(1,4)*Pos(1); ones(1,4)*Pos(2)]; % add offset of car's center
A.P_robot.XData=A.Prot_trasl(1,:)';
A.P_robot.YData=A.Prot_trasl(2,:)';
frame=getframe(gcf);
im = frame2im(frame);
[imind,cm] = rgb2ind(im,256);
if k==1
imwrite(imind,cm,'experiment.gif','gif', 'LoopCount',inf,'DelayTime',0.000001);
end
if rem(k,2)==0
imwrite(imind,cm,'experiment.gif','gif','WriteMode','append','DelayTime',0.000001);
end
drawnow
end