论文阅读笔记《Robust Feature Matching for Remote Sensing Image Registration via Locally Linear Transformin》
核心思想
该文提出一种基于局部线性变换(Locally Linear Transforming,LLT)约束的特征匹配方法用于遥感图像的对齐。首先根据特征点之间的相似性,构建一个假定的匹配点集,然后从中将误匹配点筛除出去,得到最终的匹配结果。筛除误匹配点的过程,该文将其定义为一个带有隐变量的贝叶斯模型最大似然估计问题,并引入了局部线性变换约束(LLT),采用EM算法对其求解。作者研究了三种常见的变换形式:刚性变换(rigid transform)、仿射变换(affine transform)和非刚性变换(non-rigid transform),分别给出了在三种变换条件下的计算方法。
实现过程
问题定义
首先,给出问题的定义和描述。给定一个包含 N N N对匹配点的候选匹配点集 S = { ( x n , y n ) } n = 1 N S=\{(x_n,y_n)\}_{n=1}^N S={(xn,yn)}n=1N, x n , y n x_n,y_n xn,yn分别表示两幅图像中的匹配特征点的二位坐标向量。假设正确匹配点的噪声满足各向同性的高斯分布,均值为0,方差为 σ 2 I \sigma^2I σ2I, I I I表示单位矩阵,误匹配点满足均匀分布。为每个匹配对引入一个隐变量 z n ∈ { 0 , 1 } z_n\in\{0,1\} zn∈{0,1}, z n = 1 z_n=1 zn=1表示匹配对 ( x n , y n ) (x_n,y_n) (xn,yn)是正确匹配点,反之 z n = 0 z_n=0 zn=0表示匹配对 ( x n , y n ) (x_n,y_n) (xn,yn)是错误匹配点。则在给定模型参数 θ \theta θ和点 x n x_n xn的条件下,采样得到 y n y_n yn的概率,即 y n y_n yn的条件概率模型为:
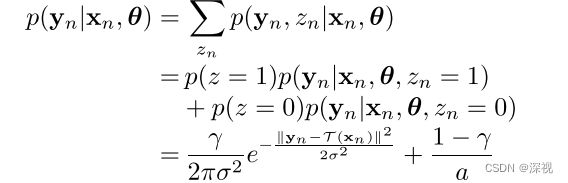
其中 θ = { T , σ 2 , γ } \theta=\{\mathcal{T}, \sigma^2, \gamma\} θ={T,σ2,γ}表示模型的参数, T \mathcal{T} T表示匹配点之间的几何变换关系,对于正确匹配点 y n = T ( x n ) y_n=\mathcal{T}(x_n) yn=T(xn); σ 2 \sigma^2 σ2表示高斯分布的方差; γ \gamma γ表示 z n = 1 z_n=1 zn=1的概率,即 p ( z n = 1 ) = γ p(z_n=1)=\gamma p(zn=1)=γ, p ( z n = 0 ) = 1 − γ p(z_n=0)=1-\gamma p(zn=0)=1−γ。 1 / a 1/a 1/a表示误匹配点的均匀分布, a a a表示第二幅图像(目标图像)的面积。对于点集的坐标向量 X = ( x 1 , . . . , x N ) T , Y = ( y 1 , . . . , y N ) T \mathbf{X}=(x_1, ...,x_N)^T,\mathbf{Y}=(y_1, ...,y_N)^T X=(x1,...,xN)T,Y=(y1,...,yN)T,假设其满足独立同分布条件,可以得到概率函数 p ( Y ∣ X , θ ) = ∏ n = 1 N p ( y n ∣ x n , θ ) p(\mathbf{Y}|\mathbf{X},\theta)=\prod_{n=1}^Np(y_n|x_n,\theta) p(Y∣X,θ)=n=1∏Np(yn∣xn,θ)则我们的求解目标则是寻找让概率函数取得最大值的模型参数 θ \theta θ,即最大似然估计 θ ∗ = arg max θ p ( Y ∣ X , θ ) \theta^*=\argmax_{\theta}p(\mathbf{Y}|\mathbf{X},\theta) θ∗=θargmaxp(Y∣X,θ),这等价于最小化负对数似然函数
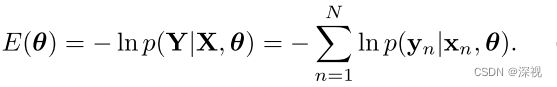
为求解上述问题,该文采用了EM算法进行求解,关于EM算法的介绍可参见这篇博客《EM算法推导小记》。构建完整数据对数似然函数 Q ( θ , θ o l d ) = ∑ n = 1 N ∑ z n p ( z n ∣ x n , y n , θ o l d ) ln p ( y n , z n ∣ x n , θ ) = ∑ n = 1 N p ( z n = 1 ∣ x n , y n , θ o l d ) ln p ( y n , z n = 1 ∣ x n , θ ) + p ( z n = 0 ∣ x n , y n , θ o l d ) ln p ( y n , z n = 0 ∣ x n , θ ) \mathcal{Q}(\theta,\theta^{old})=\sum_{n=1}^N\sum_{z_n}p(z_n|x_n,y_n,\theta^{old})\ln p(y_n,z_n|x_n,\theta)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\ \\=\sum_{n=1}^Np(z_n=1|x_n,y_n,\theta^{old})\ln p(y_n,z_n=1|x_n,\theta)+p(z_n=0|x_n,y_n,\theta^{old})\ln p(y_n,z_n=0|x_n,\theta) Q(θ,θold)=n=1∑Nzn∑p(zn∣xn,yn,θold)lnp(yn,zn∣xn,θ) =n=1∑Np(zn=1∣xn,yn,θold)lnp(yn,zn=1∣xn,θ)+p(zn=0∣xn,yn,θold)lnp(yn,zn=0∣xn,θ)上式经过展开化简,并省略去与 θ \theta θ无关的项之后可得
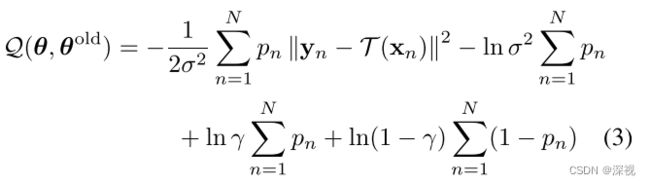
其中 p n = p ( z n = 1 ∣ x n , y n , θ o l d ) p_n=p(z_n=1|x_n,y_n,\theta^{old}) pn=p(zn=1∣xn,yn,θold)表示 z z z的后验概率,表示 ( x n , y n ) (x_n,y_n) (xn,yn)是一对匹配点的概率。EM算法的E步骤,就是在已知参数 θ o l d \theta^{old} θold的条件下,计算对数似然函数 Q ( θ , θ o l d ) \mathcal{Q}(\theta,\theta^{old}) Q(θ,θold),核心在于计算后验概率 p n p_n pn。根据贝叶斯定理,后验概率 p n p_n pn的计算过程如下 p n = p ( z n = 1 ∣ x n , y n , θ o l d ) = p ( z n = 1 ) p ( y n ∣ x n , θ o l d , z n = 1 ) p ( z n = 1 ) p ( y n ∣ x n , θ o l d , z n = 1 ) + p ( z n = 0 ) p ( y n ∣ x n , θ o l d , z n = 0 ) p_n=p(z_n=1|x_n,y_n,\theta^{old})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\ \\ =\frac{p(z_n=1)p(y_n|x_n,\theta^{old},z_n=1)}{p(z_n=1)p(y_n|x_n,\theta^{old},z_n=1)+p(z_n=0)p(y_n|x_n,\theta^{old},z_n=0)} pn=p(zn=1∣xn,yn,θold) =p(zn=1)p(yn∣xn,θold,zn=1)+p(zn=0)p(yn∣xn,θold,zn=0)p(zn=1)p(yn∣xn,θold,zn=1)计算结果经过化简约分可得
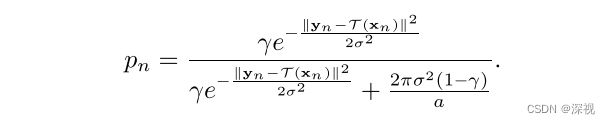
EM算法的M步骤,则是寻找新的参数 θ n e w \theta^{new} θnew使得似然函数最大化,即 θ n e w = arg max θ Q ( θ , θ o l d ) \theta^{new}=\argmax_{\theta}\mathcal{Q}(\theta,\theta^{old}) θnew=θargmaxQ(θ,θold)。令 Q ( θ , θ o l d ) \mathcal{Q}(\theta,\theta^{old}) Q(θ,θold)函数分别对 σ 2 \sigma^2 σ2和 γ \gamma γ求导,并使其导数为0,可得
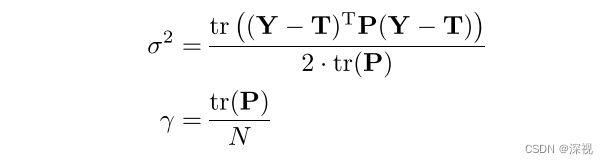
其中 T = ( T ( x 1 ) , . . . , T ( x N ) ) T \mathbf{T}=(\mathcal{T}(x_1),...,\mathcal{T}(x_N))^T T=(T(x1),...,T(xN))T,当EM算法收敛之后,我们可以求得最佳的后验概率 p n p_n pn,并根据设定的阈值 τ \tau τ,来判断 ( x n , y n ) (x_n,y_n) (xn,yn)是否属于匹配点。匹配点集 I \mathcal{I} I的定义如下
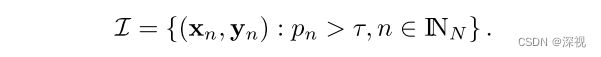
局部线性变换约束
明确了问题的定义和求解目标之后,我们就要引入本文设计的局部线性变换约束条件LLT了。该条件是基于这样的一个假设,就是匹配点附近的局部结构在经过变换 T \mathcal{T} T后仍保持不变。这是一个非常常见的假设条件,那么如何描述匹配点附近的局部结构呢?作者首先为点集 X \mathbf{X} X中的每个特征点都找到其对应的 K K K个最近邻,构建一个 N × N N\times N N×N的权重矩阵 W W W,其中的元素 W i j W_{ij} Wij描述了点集中其他的点 x j x_j xj和 x i x_i xi之间的关系,如果 W i j = 0 W_{ij}=0 Wij=0,表示 x j x_j xj不是 x i x_i xi邻域内的点。然后通过最小化重构误差的方式来计算 W W W,最小化目标函数为
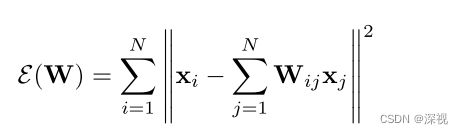
约束条件为 ∀ i , ∑ j = 1 N W i j = 1 \forall i,\sum_{j=1}^NW_{ij}=1 ∀i,∑j=1NWij=1,通过最小二乘法可以很容易得到最优的权重矩阵 W W W。那么根据上述的假设条件,我们希望变换后的点,其重构误差仍然很小,即得到一个变换损失项 ∑ i = 1 N p i ∥ T ( x i ) − ∑ i = 1 N W i j T ( x j ) ∥ 2 \sum_{i=1}^Np_i\|\mathcal{T}(x_i)-\sum_{i=1}^NW_{ij}\mathcal{T}(x_j)\|^2 ∑i=1Npi∥T(xi)−∑i=1NWijT(xj)∥2,将其与我们上文提到的似然函数 Q ( θ , θ o l d ) \mathcal{Q}(\theta,\theta^{old}) Q(θ,θold)结合起来,可得新的目标函数为
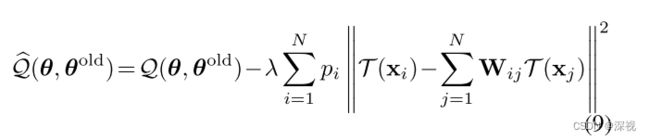
λ > 0 \lambda>0 λ>0是一个平衡参数,为了估计参数 T \mathcal{T} T,我们将上式展开,并忽略掉无关量,可得新的最小化目标函数
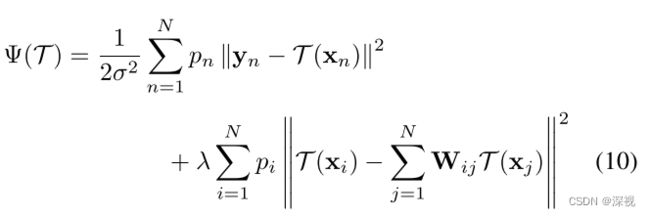
其由一个经验误差项和变换损失项构成。接下来就是根据不同的变换形式 T \mathcal{T} T来求解了,该文研究了三种变换形式分别是刚性变换、仿射变化和非刚性变换。
1. 刚性变换
对于刚性变换, T ( x n ) = s R x n + t \mathcal{T}(x_n)=sRx_n+t T(xn)=sRxn+t, R R R表示 2 × 2 2\times 2 2×2的旋转矩阵,且为正交矩阵; t t t表示 2 × 1 2\times 1 2×1的平移矩阵; s s s表示放缩系数。则优化目标函数可以写为
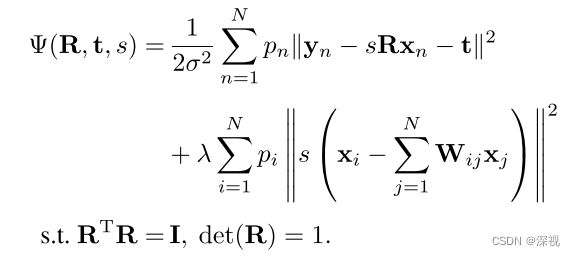
求解的推导过程,我们不再详述,感兴趣可参看原文。下面直接给出结果

其中

将 t t t带回原目标函数中,并忽略与 R , s R,s R,s无关的项可得

其中
![]()
![]()
只考虑与 R R R有关的项可得
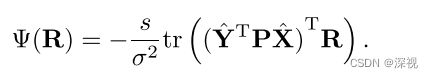
最优的 R = U D V T R=UDV^T R=UDVT,其中 U U U和 V V V可由 U S V T = s v d ( Y ^ T P X ^ ) USV^T=svd(\hat{\mathbf{Y}}^T\mathbf{P}\hat{\mathbf{X}}) USVT=svd(Y^TPX^)计算得到,而 D = d i a g ( 1 , d e t ( U V T ) ) D=diag(1,det(UV^T)) D=diag(1,det(UVT))。最后 s s s为
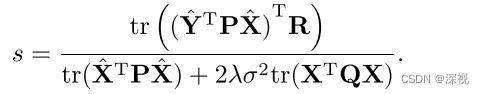
2. 仿射变换
对于仿射变换, T ( x n ) = A x n + t \mathcal{T}(x_n)=Ax_n+t T(xn)=Axn+t, A A A表示 2 × 2 2\times 2 2×2的仿射矩阵; t t t表示 2 × 1 2\times 1 2×1的平移矩阵,则目标函数为

最优的 t t t和 A A A分别为

3. 非刚性变换
对于非刚性变换,作者采用在初始坐标 x x x上加一个与坐标相关的偏移函数 f ( x ) f(x) f(x)来描述变换 T ( x ) = x + f ( x ) \mathcal{T}(x)=x+f(x) T(x)=x+f(x),函数 f ( x ) f(x) f(x)属于一个特定的函数空间 H \mathcal{H} H,即为一个再生核希尔伯特空间(RKHS)。作者使用对角化高斯核函数 Γ ( x i , x j ) = κ ( x i , x j ) ⋅ I = e − β ∥ x i − x j ∥ 2 ⋅ I \Gamma(x_i,x_j)=\kappa(x_i,x_j)\cdot I=e^{-\beta\|x_i-x_j\|^2}\cdot I Γ(xi,xj)=κ(xi,xj)⋅I=e−β∥xi−xj∥2⋅I来定义空间 H \mathcal{H} H。则最优的非刚性变换 T \mathcal{T} T可得
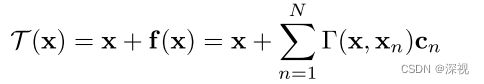
c n c_n cn表示系数,其由一个线性系统确定
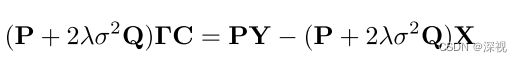
其中 C = ( c 1 , . . . , c N ) T C=(c_1,...,c_N)^T C=(c1,...,cN)T。作者还给出了一种稀疏得快速近似求解方法,这里就不赘述了。
创新点
- 将特征点匹配问题定义为一个最大化似然估计问题,并通过EM算法进行求解
- 引入了局部线性变换约束
- 针对刚性变换、仿射变换和非刚性变换给出了求解方法
算法评价
抛开外在的求解形式,本文还是采用一个局部的线性变换约束来筛选出匹配的点,对于变换损失项过大的点会分配一个更低的匹配概率。将概率与匹配问题结合起来,通过最大化似然估计的方式来寻找匹配点的方式还是一种比较新颖的思路。
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。