Matlab实现常见的插值算法

本文介绍如何使用 Matlab 实现常见的插值算法：分段三次埃尔米特插值和三次样条插值。

分段三次埃尔米特插值

(1) pchip（x, y, new_x）函数表示分段三次埃尔米特插值，x表示已有的数据 点，y表示数据点代表的纵坐标值，new_x表示从哪些点进行插值

(2) plot函数用法 plot(x1,y1,x2,y2)

线方式： - 实线 :点线 -. 虚点线 - - 波折线

点方式： . 圆点 +加号 * 星号 x x形 o 小圆

颜色： y黄； r红； g绿； b蓝； w白； k黑； m紫； c青

x = -pi:pi; y = sin(x); 
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
figure(1); 
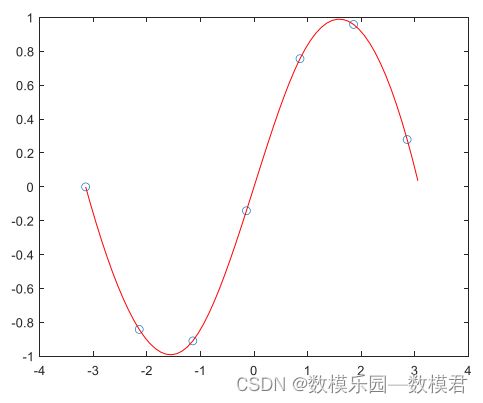
plot(x, y, 'o', new_x, p, 'r-')

三次样条插值

spline(x,y,new_x); 表示三次样条插值

x = -pi:pi; 
y = sin(x); 
new_x = -pi:0.1:pi;
p2 = spline(x,y,new_x); %三次样条插值
figure(2);
plot(x,y,'o',new_x,p2,'b-')

扩展：n 维数据的插值

interp1(x, y, xi, ‘method’)函数

x = -pi:pi; y = sin(x); 
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
figure(3);
plot(x, y, 'o', new_x, p, 'r-')

 

总结

(1) 观察以上生成的插值图像，可以看出三次样条插值更加平滑

(2) interp1 函数可以通过改变 method 参数实现多种插值方法