对抗样本(二)L-BFGS
文章目录
- 一、论文相关信息
-
- 1.论文题目
- 2.论文时间
- 3.论文文献
- 二、论文背景及简介
- 三、论文内容总结
- 四、论文所使用的符号及数据等信息
- 五、论文主要内容
-
- 1、第一个特征 神经元的语义信息
- 2、第二个特征 神经网络的盲点
- 五、实验结果
- 六、模型的不稳定性分析
- 七、总结
一、论文相关信息
1.论文题目
Intriguing properties of neural networks
2.论文时间
2014年
3.论文文献
https://arxiv.org/abs/1312.6199
二、论文背景及简介
深度学习因为其表达能力强而获得了成功,但也造成了其会学习到一些无法解释的结果,具有一些反常理的属性。一、单个高阶单位和随机线性组合的高阶单位之间没有区别,这表明,在神经网络的高层中,包含语义信息的是空间,而不是单个单元。二、深度神经网络学习的输入输出映射在很大程度上是不连续的,这造成了我们可以通过应用某种难以察觉的扰动使网络误分类图像,这种扰动是通过最大化网络的预测误差而发现的。
三、论文内容总结
- 提出了两个神经网络的有趣的特征—神经元的语义信息与神经网络的盲点
- 通过控制输入来最大化激活神经元,来获取神经元的语义信息
- 神经网络在添加较小扰动时,会使其分类错误
- 我们可以通过最大化分类错误率来获得扰动,其公式如下:
m i n c ∣ r ∣ + l o s s f ( x + r , l ) s . t . x + r ∈ [ 0 , 1 ] m min \ \ c|r|+loss_f(x+r,l) \\ s.t. \ \ x+r \in [0,1]^m min c∣r∣+lossf(x+r,l)s.t. x+r∈[0,1]m
- 可以通过L-BFGS来找到近似解
- 对抗样本是一种普遍现象,并不是由于模型的过拟合与特定的数据集的引起的,其具有泛化能力
- 对抗样本引入到训练过程中是可以提高模型的泛化能力
- 作者认为,扰动会在神经网络正向传播的过程中,不断地累加,直到最后变得很大,大到能够使其越过了分类边界。
- 作者认为,对抗样本时因为网络的离散性,才会出现的(后面的论文中与该观点持相反意见,其认为是网络的过度的线性才导致的对抗样本的出现)
附:如需继续学习对抗样本其他内容,请查阅对抗样本学习目录
四、论文所使用的符号及数据等信息
符号
x \ x x代表术语的图片, ϕ ( x ) \ \phi(x) ϕ(x)代表某一层的激活值。
数据集及模型
在MINST数据集下
一个简单的全连接层,使用Softmax分类器,把这个网络称为FC
在自动编码器上训练的分类器,把这个网络成为AE
在ImageNet数据集下
使用了AlexNet
在10MYoutube数据集下
无监督训练网络,称为QuocNet
参数
在MINST数据集实验中,使用了权重衰减,参数为 λ \ \lambda λ。在一些实验中,将MINST数据集分离为 P 1 和 P 2 \ P_1和P_2 P1和P2。
五、论文主要内容
该论文实际是描述了神经网络的两个特征
1、第一个特征 神经元的语义信息
论文中所提到的神经网络的第一个特征是神经网络中各个单元的语义信息。
在之前的工作中,通过控制输入图像来最大化激活给定的单元,来分析每个单元的语义信息。而这些工作也显示出,最后一层layer是分类的基础,对语义信息是最有帮助的。他们,对激活单元 ϕ ( x ) \ \phi(x) ϕ(x)的随机投影,发现这样并没有表现出语义信息。这也就表明,神经网络并不是通过坐标系来构建语义信息。一般来说,是整个激活空间包含了语义信息的主体,而并非单个的单元。 在空间旋转后,向量表示仍然是稳定的,也就是说是整个向量包含着语义信息,而并非向量中的某个单元。
在下文中,作者通过实验,进行了说明。
以神经网络的某一层i为例,我们通过改变输入来找到能够最大化激活该层的输入图像 x ′ \ x' x′,我们已知第i层的隐向量为 e i \ e_i ei。可以将 x ′ \ x' x′进行如下表示:
x ′ = a r g m a x x ∈ L ( ϕ ( x ) , e i ) x' = arg max_{x\in L}(\phi(x),e_i) x′=argmaxx∈L(ϕ(x),ei)
在这里 L \ L L表示验证集。
之后,将 e i \ e_i ei换成了随机的向量 v \ v v,而实验结果表明,找到的图像 x ′ \ x' x′都是差不多的,也就是说,随机的向量并不包含语义信息,这就说明,神经网络并购不是通过坐标系来分开变量因素的。
这些实验仅仅表明了,在一个特定的输入分布的子集中,神经单元的生成不变性的能力,但这并没有解释域内的其他部分。在第二个特征中将会对这部分进行讲解,即神经网络的盲点。
2、第二个特征 神经网络的盲点
第二个特征就是本文要讲解的对抗样本的内容,即神经网络对输入样本的小扰动的稳定性
这些扰动是通过最大化分类错误率来生成的,这个小扰动可以让神经网络误分类该图像,而且扰动具有可迁移性。
这些结果表明,由反向传播训练出来的网络具有一些非直观的特征和内在的盲点,这些结构也是跟数据分布相关的。
论文表示,输出层有可能会将一些不重要的概率分配给输入空间的一些区域,而这些区域是训练样本没有覆盖的地方。而这些区域,在不同的视角看,可能能表示相同的物体,但在像素空间中距离很远(即我们肉眼可分辨的不同物体),却在输出域中共享着相同的标签和结构。
需要注意,通过简单的随机取得的扰动是没有用的,他仍然会被正确分类,得到的图像与原来的图像仍然是高度相关的。对抗样本是精心设计出来的。所以,通过增加小的扰动来扩充数据集是没有太大效率的。
那该如何找到对抗样本呢?作者给出了如下的box-constrained优化问题
x 为 输 入 样 本 , l 为 攻 击 的 目 标 标 签 , f 代 表 神 经 网 络 , r 为 扰 动 , m 代 表 输 入 样 本 的 维 度 m i n ∣ ∣ r ∣ ∣ 2 s . t . f ( x + r ) = l x + r ∈ [ 0 , 1 ] m x为输入样本,l为攻击的目标标签,f代表神经网络,r为扰动,m代表输入样本的维度 \\ min \ \ ||r||_2 \\ s.t. \ \ f(x+r)=l \\ x+r \in [0,1]^m x为输入样本,l为攻击的目标标签,f代表神经网络,r为扰动,m代表输入样本的维度min ∣∣r∣∣2s.t. f(x+r)=lx+r∈[0,1]m
一般来说,可以满足这个条件的r不是唯一的,我们用 D ( x , l ) \ D(x,l) D(x,l)来表示一个最小的r。但是,要想要找到这样的扰动D,是十分困难的,作者使用了box-constrained的L-BFGS来近似它。作者通过执行线搜索来找到下列问题的最小r满足 f ( x + r ) = l \ f(x+r)=l f(x+r)=l的最小 c > 0 \ c>0 c>0,从而找到 D ( x , l ) \ D(x,l) D(x,l)的近似值。
m i n c ∣ r ∣ + l o s s f ( x + r , l ) s . t . x + r ∈ [ 0 , 1 ] m min \ \ c|r|+loss_f(x+r,l) \\ s.t. \ \ x+r \in [0,1]^m min c∣r∣+lossf(x+r,l)s.t. x+r∈[0,1]m
如果目标函数是凸的,那么我们可以找到r的精确解,但是一般来说神经网络一般都是非凸的,所以我们只能找到近似解。
对抗样本是一种普遍现象,并不是由于模型的过拟合与特定的数据集的引起的。同时,作者认为,将对抗样本引入到训练过程中是可以提高模型的泛化能力。
五、实验结果
实验结果如下
行表示对抗样本,列代表模型,数字表示对抗成功率(模型分类的错误率)
2、不同的训练集,不同模型间的对抗样本

行表示对抗样本(由训练集1训练得到),列代表模型(由训练集2训练得到)
第二个模块是作者对对抗样本做出的优化,将标准差提升到0.1,使用 x + 0.1 ⋅ x ′ − x ∣ ∣ x ′ − x ∣ ∣ 2 \ x+0.1·\frac{x'-x}{||x'-x||_2} x+0.1⋅∣∣x′−x∣∣2x′−x作为对抗样本,而不用x’
六、模型的不稳定性分析
作者表示,对抗样本之所以会让模型分类错误,是因为误差具有累加性,对抗样本在输入图片上有一个小误差,在网络的每一层都会使误差变大,到了网络了最后一层,于是便让网络分类错误。本节就是对该问题进行分析。
用 ϕ ( x ) \ \phi(x) ϕ(x) 表示K层网络的输出,用 ϕ i ( x ; W i ) \ \phi_i(x;W_i) ϕi(x;Wi) 表示第i层的输出,则:
ϕ ( x ) = ϕ K ( ϕ K − 1 ( . . . ϕ 1 ( x ; W 1 ) ; . . . W k − 1 ) ; W k ) \phi(x) = \phi_K(\phi_{K-1}(...\phi_1(x;W_1);...W_{k-1});W_k) ϕ(x)=ϕK(ϕK−1(...ϕ1(x;W1);...Wk−1);Wk)
模型 ϕ ( x ) \ \phi(x) ϕ(x) 的不稳定性可以用Lipschitz上界来描述,即存在常数 L k \ L_k Lk ,使得:
∀ x , r , ∣ ∣ ϕ k ( x , W k ) − ϕ k ( x + r , W k ) ∣ ∣ ≤ L k ∣ ∣ r ∣ ∣ 累 积 可 得 ∣ ∣ ϕ ( x ) − ϕ ( x + r ) ∣ ∣ ≤ L ∣ ∣ r ∣ ∣ , L = ∏ k = 1 K L k \forall x,r\ \ ,||\phi_k(x,W_k) - \phi_k(x+r,W_k)||\le L_k||r|| \\ 累积可得 ||\phi(x) - \phi(x+r)||\le L||r|| \ \ ,L=\prod_{k=1}^{K}L_k ∀x,r ,∣∣ϕk(x,Wk)−ϕk(x+r,Wk)∣∣≤Lk∣∣r∣∣累积可得∣∣ϕ(x)−ϕ(x+r)∣∣≤L∣∣r∣∣ ,L=k=1∏KLk
relu层、池化层、全连接层、池化层都是收缩的(即满足上式)。因此,作者做出了实验,得到结果如下
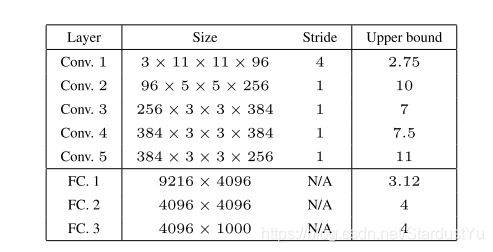
从结果可以看出,网络是不稳定的,在第一层卷积层就出现了不稳定的情况。但是,作者证明,大的上界并不会自动转换成对抗样本,但是小的上界可以防止对抗样本的产生。
这也说明,对参数的简单的正则化就可以提升模型的泛化能力。
七、总结
该篇文章主要讲述了神经网络的两个反常的特性,分别是由于神经元的语义和圣经网络的离散型导致。对抗样本的存在说明了网络的泛化能力不高。
