如何解决过拟合/欠拟合

前言

机器学习的基本问题是利用模型对数据进行拟合，学习的目的并非是对有限训练集进行正确预测，而是对未曾在训练集合出现的样本能够正确预测。

模型对训练集数据的误差称为经验误差，对测试集数据的误差称为泛化误差。

模型对训练集以外样本的预测能力就称为模型的泛化能力，追求这种泛化能力始终是机器学习的目标

过拟合(overfitting)和欠拟合(underfitting)是导致模型泛化能力不高的两种常见原因，都是模型学习能力与数据复杂度之间失配的结果。

“欠拟合”常常在模型学习能力较弱，而数据复杂度较高的情况出现，此时模型由于学习能力不足，无法学习到数据集中的“一般规律”，因而导致泛化能力弱。、

与之相反，“过拟合”常常在模型学习能力过强的情况中出现，此时的模型学习能力太强，以至于将训练集单个样本自身的特点都能捕捉到，并将其认为是“一般规律”，同样这种情况也会导致模型泛化能力下降。

过拟合与欠拟合的区别在于，欠拟合在训练集和测试集上的性能都较差，而过拟合往往能较好地学习训练集数据的性质，而在测试集上的性能较差。

在神经网络训练的过程中，欠拟合主要表现为输出结果的高偏差，而过拟合主要表现为输出结果的高方差。

过拟合

过拟合是指学习时选择的模型所包含的参数过多，以至于出现这一模型对已知数据预测得很好，对未知数据预测的很差的现象。

过拟合出现原因

• 建模样本选取有误，如样本数量太少，选样方法错误，样本标签错误等，导致选取的样本数据不足以代表预定的分类规则
• 样本噪音干扰过大，使得机器将部分噪音认为是特征从而扰乱了预设的分类规则
• 假设的模型无法合理存在，或者说是假设成立的条件实际并不成立
• 参数太多，模型复杂度过高
• 对于决策树模型，如果我们对于其生长没有合理的限制，其自由生长有可能使节点只包含单纯的事件数据(event)或非事件数据(no event)，使其虽然可以完美匹配（拟合）训练数据，但是无法适应其他数据集
• 对于神经网络模型：
  对样本数据可能存在分类决策面不唯一，随着学习的进行,，BP算法使权值可能收敛过于复杂的决策面；
  b)权值学习迭代次数足够多(Overtraining)，拟合了训练数据中的噪声和训练样例中没有代表性的特征

解决方法

1. 正则化方法

正则化方法是指在进行目标函数或代价函数优化时，在目标函数或代价函数后面加上一个正则项，一般有L1正则与L2正则等。

• L1正则：
  

L1正则即在原有的损失函数的基础上添加参数向量的L1范数，正则项的系数用于平衡原有损失函数和正则项之间的关系。

• L2正则
  

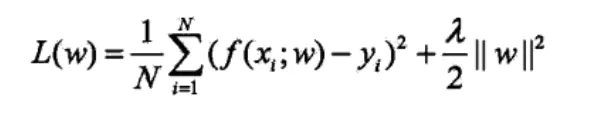
L2正则即在原有的损失函数的基础上添加参数向量的L2范数。

在损失函数中添加正则项符合奥斯卡姆剃刀原理：在所有可能选择的模型中，能够很好解释已知数据并且十分简单的模型才是最好的模型。

2. 交叉验证

如果给定的样本数据充足，进行模型选择的一种简单方法是随机地将数据集切分为三部分，分别为训练集，验证集和测试集。

训练集用来训练模型，验证集用于模型的选择，测试集用于方法的评估。

在学习到不同复杂度的模型中，选择对验证集有最小预测误差的模型。

交叉验证有以下几种方法：

1、简单交叉验证
随机地将已给数据分为两部分，一部分作为训练集，一部分作为测试集，然后用训练集在各种条件下训练模型，从而得到不同的模型，在测试集上评价各个模型的测试误差，选出测试误差最小的模型。

2、S折交叉验证
首先随机地将已给数据切分为S个互不相交的大小相同的子集，然后利用S-1个子集的数据训练模型，利用余下的子集测试模型，将这一过程对可能的S种选择重复进行，最后选出S次评测中平均测试误差最小的模型。

3、留一交叉验证
S折交叉验证的一种特殊情况，即S=N（N为训练集样本的数量）

3. Early stopping

对模型进行训练的过程即是对模型的参数进行学习更新的过程，这个参数学习的过程往往会用到一些迭代方法，如梯度下降（Gradient descent）学习算法。

Early stopping便是一种迭代次数（epochs）截断的方法来防止过拟合，即在模型对训练数据集迭代收敛之前停止迭代来防止过拟合。

具体做法是，在每一词迭代结束时（一个迭代集为对所有的训练数据的一轮遍历）计算验证集的accuracy，当accuracy不再提高时，就停止训练。

在训练的过程中，记录到目前为止最好的validation accuracy，当连续10次迭代（或者更多次）没达到最佳accuracy时，则可以认为accuracy不再提高了。此时便可以停止迭代了。这种策略也称为“No-improvement-in-n”，n即迭代的次数，可以根据实际情况取，如10、20、30……

4. 数据集扩充

在数据挖掘领域流行着这样的一句话，“有时候往往拥有更多的数据胜过一个好的模型”。

训练数据与将来的数据是独立同分布的
  
一般有以下方法：

• 从数据源采集更多数据
• 复制原有数据并加上随机噪声
• 重采样
• 根据当前数据集估计数据分布参数，使用该分布产生更多数据等

5. Dropout

Dropout方法是通过修改ANN中隐藏层的神经元个数来防止ANN的过拟合。

欠拟合

“欠拟合”常常在模型学习能力较弱，而数据复杂度较高的情况出现，此时模型由于学习能力不足，无法学习到数据集中的“一般规律”，因而导致泛化能力弱。

欠拟合出现原因

• 模型复杂度过低
• 特征量过少

常见解决方法

• 增加新特征，可以考虑加入进特征组合、高次特征，来增大假设空间
• 添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强
• 减少正则化参数，正则化的目的是用来防止过拟合的，但是模型出现了欠拟合，则需要减少正则化参数
• 使用非线性模型，比如核SVM 、决策树、深度学习等模型
• 调整模型的容量(capacity)，通俗地，模型的容量是指其拟合各种函数的能力
• 容量低的模型可能很难拟合训练集；使用集成学习方法，如Bagging ,将多个弱学习器Bagging

参考文章

过拟合
欠拟合和过拟合出现原因及解决方案