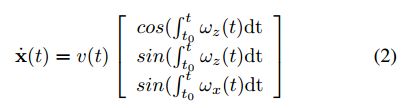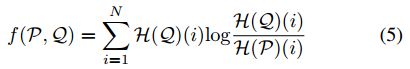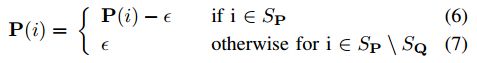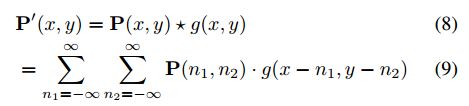【论文翻译】Road vehicle localization with 2D push-broom LIDAR and 3D priors 论文学习笔记

采用二维推扫激光雷达和三维先验地图进行道路车辆的定位

本文是2012.5年发表的EI会议（ICRA）

作者：

Ian Baldwin
Department of Engineering Science
Oxford University
Oxford, UK
Email: [email protected]

Paul Newman
Department of Engineering Science
Oxford University
Oxford, UK
Email: [email protected]
 

目录

摘要

1、引言 introduction

2、相关工作 related work

3、概述 overview

4、定位 LOCALIZATION

5、校准问题 CALIBRATION ISSUES

6、结果

7、讨论

8、结论

9、致谢

---

摘要

本文中，我们介绍论证了一种方法：通过单个的推扫式2D激光雷达，借助于先验3D感知来精确地定位道路车辆。相比于传统的扫描匹配，我们的雷达是朝向下方的，从而引起持续的“地面撞击”。我们的方法借此产生了一个小的3D感知带，其可以和先验3D感知相匹配。这个3D感知带的产生是根据对车辆速度的实时估计。理论上，这些估计信息可以从车辆的速度里程计获得，但实际上，这些来自于里程计的数据是有偏差的，我们因此还提供了从3D感知数据修正该偏差的方法。我们证实了，我们设计的的低成本的系统胜于高标准的积分式DGPS/IMU系统——在以测试场中超过26km的行驶路径为测试条件时。

1、引言 introduction

本文是关于：使用激光雷达，来实现对道路车辆的精确定位。我们的关注点是：低成本的先验3D环境拓展更新，用的是单个2D推扫式（push-broom）激光雷达——一个安装好的2D激光雷达，车辆载着它推扫过周围的环境，以此来产生数据。

我们的研究动机（motivation）是因为目睹了很多低成本的车辆使用和共享昂贵的单次生成地图。为了达到这个目的我们的定位计划没有使用3D激光雷达、微分式GPS和积分式惯性导航系统。和这些系统相比，我们将展示我们的系统将如何胜过一个商用级的IMU系统——在26km的驾驶距离下。

一个直接的问题是为什么要使用3D地图？简单的2D扫描匹配还不够吗？我们的经验使我们得到否定的结论。横摇和纵摆、来自各种地面凸起的撞击和刮擦使得系统变得脆弱。事实上，正是为了试图在传统的扫描匹配技术中适应地面撞击，才有了我们本文中的工作。我们有意地将我们的激光雷达朝向下方，来找出可能会发生的地面撞击。通过积分估计车辆的动作，我们可以用雷达的数据形成一个3D感知带。稠密的最新数据，也即新形成的3D感知带，可被连续的融入3D点云总地图，通过匹配将3D感知带作为补丁打上去。现在的关键问题，就转为了如何估计车辆的运动。

三轴MEMS的陀螺仪是当今广泛适用的，能提供一个廉价的方式来估计角度值。然而，速度剖面相对较难得到。根据法律规定，道路车辆的测速仪都具有指示速度的功能，我们可以立即从测速仪上得到指示速度。然而，由于一些显而易见的原因，这些设备往往高估了速度，因此在本文中，我们也承认，我们有可能必须在线校准速度反馈。我们通过激光扫描扇面检测道路标记的通过情况，并通过(动态规划)推导出检测到的反射率信号与预先测量预测的信号之间的偏差，从而恢复车辆速度。

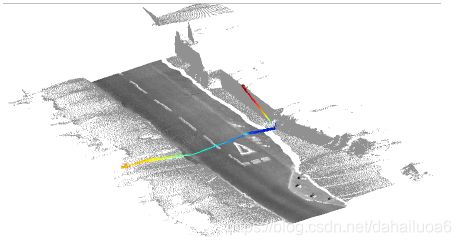
有人可能会说，DGPS和IMU系统最终将变得价格低廉，因此有更广泛的应用。虽然事实的确如此，但人们仍然需要担心这些系统的运行范围——特别是在没有良好的DGPS接收的地区。作为说明，请参考图1。这张图显示的是我们在Begbroke测试场地周围收集了本文使用的26公里数据:

图1:环绕牛津Begbroke站点的环路，对比GPS接收良好的区域(右图)与较差的区域(底部部分，浓密的树叶之间)，较差地区会产生较大的惯性导航系统估计误差。左下角显示的是全局原点。本文所使用的26公里数据都是围绕着这个地点收集的。

图1所示为一个高品质OxTS 惯性导航系统系统穿过科学园时的轨迹。请注意，在没有被树叶和建筑物遮挡的路段(主要是东北和西部路段)，性能良好，估计的车辆路径符合道路形状。然而，在南部地区，一小片树林阻碍了DGPS的校正，导致惯性导航系统估计的路径与道路严重偏离——这种问题在我们自行设计的系统中是没有出现的。

2、相关工作 related work

基于激光、采用先验地图的道路车辆室外定位最近被几位学者进行了研究。

○在[1]中，作者通过驱动三维激光传感器(Velodyne)以及GPS、IMU和里程计数据离线生成精确的地图。此地图中的定位通过粒子滤波器来执行。虽然这项工作在思路上与我们的方法最为相似，但我们不需要昂贵的、驱动传感器或离线缓和期来生成地图。此外，激光数据的性质要求我们采用完全不同的目标函数。在[2]中，研究者继续扩展了这项工作，开发了一个长期的概率性框架（probabilistic framework），再次使用了Velodyne。

○Kummerle等人[3]开发了一个自主系统，该系统利用Velodyne获得的多层次地表地图，以2.5D的结构表示环境。

○最近，[4]在一个SLAM框架中使用了Velodyne。

○在[5]的作者利用一个2D的道路网络地图和激光，结合一个支持DGPS的接收器来估计姿态。

同样，我们寻求消除对昂贵的、高校准强度的设备(如Velodyne)或持久GPS信号的需求，以便进行长期导航。

○在[6]中，作者利用一个鲁棒的ICP[7]算法进行局部扫描匹配，并结合直方图特征表示来匹配局部子映射。

○在[8]中，同样的作者利用旋转扫描激光来生成三维点云图。（In [8], the same authors utilize a rotating, scanning laser in order to generate 3D point-clouds maps.）

在我们这项工作中，我们采取了一种故意降低激光来观察地面打击的方法，因此避免了使用ICP方法，因为考虑到光束的扫描模式，ICP方法会产生多个局部极小值。

○机载激光条带成像(ALSM)[9]是地球成像领域的一个相关概念，它利用类似的条带生成技术来生成一致的环境模型——然而，该系统不用于定位，而是使用惯性导航系统数据进行地图融合。

○Visual Teach and Repeat[10]是一个类似的基于视觉的系统，其中使用一个立体摄像机构建一个由以前访问过的子映射(Teach阶段)组成的流形映射，然后在随后的定位遍历中使用该子映射(Repeat)。

我们的方法的不同之处在于，除了减轻对特征识别的需要之外，我们还利用了主动传感技术来降低对光照/光照变化的敏感度。VT&R（Visual Teach and Repeat）也表现出相对较小的“收敛盆地”，这一点与我们的方法不同。

3、概述 overview

我们将把通过工作空间的点云采集作为一种“经历（experience）”，包括激光扫描、姿态、速度(角度和线性)和加速度。我们采用这个术语是为了强调我们的道路定位任务不需要全局正确的度量地图。我们只是希望根据先前经验定义的轨迹和点云来定位我们自己——在这种情况下，先前经验来自于事先在城市道路上的行驶。当然，这并不排除针对度量完美的轨迹进行本地化的情况——已经通过带有回环检测等的全局优化进行了调整——我们只是不需要这种程度的准备。我们假设我们可以进行车辆运动估计并生成一个三维点云，我们将其称为P。

在第四节中（Section IV），我们将详细描述如何使用二维激光数据流来推断车辆的运动。在此之前，它为我们提供了可以通过仔细的校准和定时而提前获得的详细信息。图2说明了如何连续地下降视图来生成工作区的详细本地视图。还要注意高度反光的道路标记，这些标记在激光照射下清晰可见。该图还强调了一个明显的观点，即一个单一的2D扫描将不足以定位车辆-有一个明显的前后方向的模糊，尽管路边有明显的起伏。我们将需要建立一个激光感知带，捕捉足够的细节，以锚定自己在“感知经历（survey experience）”中的位置。

图2：下降的2D激光器(在激光下)在经过Begbroke的一段路程并产生一条感知带(运动方向是从左上角到右下角)时的单次扫描的透视图。高光扫描(根据高度着色)清楚地显示了这个方向如何捕捉道路和车辆周围边缘的起伏。感知带已使用2D扫描收集的反射率数据着色。正如所料，高反射(通过设计)的道路标志可以清楚地看到。这个信号将在后面的第五节中使用，以推导车速表读数中的车辆速度和该速度值和真实值之间的偏差。

4、定位 LOCALIZATION

图3显示了3D点云地图P的俯视图，地图P在“经历（experience）”中得以构建，覆盖了Begbroke。右边显示的是一个范例感知带Q，它通过计算车辆的位姿而生成，借助于一个“回顾窗”[t(k),t(k-N)]，此处N是窗口的长度，以秒为单位。跟踪的问题在于，给定了点云P，和在运行器件获取到的感知带Q，需要建立一个最优化的转换关系T，使得两者以最优的方式融合在一起。但是如果我们不知道车辆的动作，我们如何生成感知带Q呢？

图3:3D点云P的俯视图，覆盖在Begbroke站点上。点按高度着色，蓝色(深色调)最低，红色(浅色调)最高。显示在右边是一个范例感知带Q。注意不同的彩色地图,强调：我们的任务是确定最优的Q和P之间的对应。请注意，为了便于说明，这些图像之间的比例是不同的，并且必须用颜色来查看。

1）感知带的生成：为了在运行时，生成感知带Q，我们需要重建“回顾窗”期间的车辆动作。我们定义一个时间t的激光扫描如下：

s(t)={r1,……,r541,i1,……,i541}

其中，rn意味着激光光束n在扫描s(t)中的激光测距值（单位：m），in意味着光束的强度，S={s(1),……,s(n)}是指若干个这样的扫描扇面。此外我们开可以通过陀螺仪感知到车辆绕着3各坐标轴的旋转速度（roll pitch yaw）。考虑到车辆的转动速度和前进速度，我们能够积分状态方程：

为了得出SE2位姿x(t)（包括笛卡尔坐标系下的位置和姿态），我们可以从x(t)求出激光雷达点S(t)，从而产生感知带Q。从原则上来看，该任务很简单，但在实践中，细节占主导地位，特别是要确保陀螺仪和激光之间的时间同步非常精确——这是我们在论文第5部分讨论的内容。此外，注意我们对车辆速度v有所依赖——这也是本文的一个重点。先把这些问题放在一边，使Q与P最佳对齐的变换取决于当前的位姿x(t)。我们现在必须定义“最佳”。

2）点云的融合：一旦我们在“回顾窗”期间构造了感知带Q，那么现在就有必要去解决它和点云P的融合问题。我们寻找转换T^来实现P和Q的最佳融合——通过使得目标函数f取最小值：

正如我们所看到的，在调查（survey）中引用的感知带是角旋转速率剖面、速度剖面、激光扫描和我们寻求的SE2转换的函数。它的生成可以被分解为：

式4给出了感知带点云Q的计算过程，并应用变换T将其投影到全局框架中。P和Q都是空间中点的分布。Kullback-Leibler散度（divergence）为比较这两种分布提供了一种自然的方法，并构成目标函数 f 的基础。我们定义运算子H(.)来代表直方图函数，并将此操作应用于我们的调查和假设的感知带(是一个关于T的函数)，K-L散度（divergence）是：

其中N是分布的基数，i是迭代器 over bins（用于“数据箱”）。注意，如果我们只需要平移和旋转，那么我们可以简单地将点投射到全局XY平面中以生成直方图。

用点云的投影概率分布来表示点云是捕获环境结构的一种自然方法。棱柱状结构，如墙，由于经常被观察到，用更高的密度来表示。地面上的点自然密度较低，但仍能提供有关道路形状和结构的信息。使用这种方法，KL散度（divergence）是表示这些分布之间距离的一种自然方法，前提是它们被良好地定义——这是我们现在必须考虑的一个细节。

为了防止无限发散（divergence），我们对概率分布应用“绝对折扣”（absolute discounting）。对于计数得到的任意两个概率分布P和Q，将非零的“数据箱”（non-zero bins）集合分别定义为SP和SQ，我们将光滑概率分布P定义为:

“绝对折扣”（absolute discounting）降低了分布P在所有非零箱（方程(6)）的概率质量（probability mass），这个质量被重新分配到质量低于Q，而不是P的容器/数据箱中（这是一个“集合差”，用公式7中的运算符\表示）。这是必要的——为了使散度测量被正确地定义。最后一步，根据我们对这个目标函数的优化经验，我们在优化过程中对P和Q都应用了离散高斯卷积：

对Q而言也是类似的。上式中，g (x, y) = N(0,σ)。这种操作大大有助于提高代价函数的平滑性(在本文第六节中讨论)。

算法1详细描述了优化过程。该算法以“经历（experience）”过程中采集到的点云数据、候选感知带和所需要的转换关系Tguess (一个SE2姿势)的初始估计，以上这些量作为输入。

直方图粒度c被初始化为一个默认值，优化的停止条件被设置为无穷大。第7行使用直方图操作生成输入点云数据的离散概率密度函数(probability density function缩写pdf)，数据箱的数量由第二个参数决定。第11行定义优化过程中使用的代价函数（cost function）。该函数将两个概率分布作为输入，并返回它们之间的KL散度（KL-divergence）。

算法1：代价函数优化

在每次迭代中(第17行)，粒度都增加一个数量cdelta，以提供“退火效果”（annealing effect）。停止测量，δ，是前一个SE2估计值与当前估计值之间的差值，一旦该度量值达到预定义值，优化就停止。两个位姿之间的差异由[11]中的度量规则来测量，其中SE2位姿的方向用复数表示：

其中a和b是角的复分量。欧几里得度量现在对于比较SE2中的两个姿势是有效的。

3）位姿预测：在下一个离散区间，我们会观测到更多的转速和线速度数据，需要算法1的位姿种子来启动搜索过程。为了得到这个估计，我们应用速度，通过系统状态方程，之后将x(tk - 1)使用作为一个姿态猜测。

5、校准问题 CALIBRATION ISSUES

A. Timing 时间对齐

至关重要的是在陀螺仪、激光传感器和速度计上的时钟感知到的时间之间进行计时校准。这些时钟之间的不一致将导致点云显示“模糊”。考虑到感知带Q的信息内容，这种模糊会使目标函数变平，使得优化更加困难。

我们使用了TICSync[12]定时算法，它学习时钟之间的概率映射，并能够恢复偏差。图4显示的是经过ticsync校正的数据(左侧)，以及计时误差为正态分布50ms的相同数据(右侧)。在右图中可见到激光空间的重影随着时间误差的增加而增加。

图4：Begbroke场地周围道路标志的俯视图。与具有正常分布的50ms错误的类似点云相比，使用ticsync校正时间生成的点云如图左侧所示。修正后的点云不再有鬼影（鬼影在右侧的图像中可见）。

B.速度计偏差：离线校准

到目前为止，我们假设方程(4)右边的所有项都是已知的，特别是v(t)是可从车上的车速计中得到的。一般来说，车速计通常被事先配置为高估车速，因此我们需要补偿一个恒定的偏置项来抵消误差。因此，我们将讨论一个校准过程，在此过程中，我们试图从观测到的速度数据中恢复出来这个偏置因子。我们立即得到我们已经开发的代价函数，并使它成为一个未知速度偏差的函数。在此过程中，我们将通过缩放在测试阶段观察到的速度、并产生与之对应的缩放后的候选感知带点云Q来估计这个因子。之后，我们的校准任务就是找到转换关系T^和偏差量τ^，以使得Q最好地融入到参考点云P：

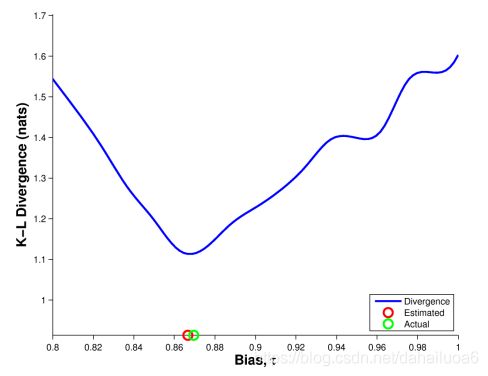
图5展现了该过程的结果：

图5：速度计偏差校准结果的说明。我们运用不同修正因素,τ,给观察到的速度——因此感知带的大小——在训练期间,和记录发现每个因素的最好位姿匹配的最低成本（and record the minimum cost of the best pose match found for each factor）。我们使用所有偏置值的最佳估计值来校正速度计的偏置。

我们故意用已知的偏置破坏地面真值速度，并使用上述方法估计校正因子。对于本文给出的结果，真实偏差设置为1.15，因此补偿这个过高估计所需的值为∼.87。在我们的分析中，我们使用了0.865的估计修正系数，并表明尽管产生了速度误差，我们仍然可以成功地跟踪超过26公里的数据。注意，这种校准技术只在匀速行驶时才有效，这在一定程度上是规定死的。

C.速度计偏差:在线校准

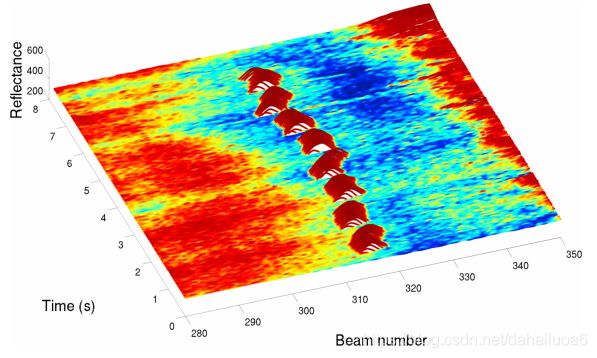
除了刚才描述的方法，还有另一种方法——从长远来看，这种方法可能会帮助我们完全摆脱对速度反馈的要求，并就眼前来看免除以恒定速度驾驶的需要。此外，它提供了一个机会，在整个车辆的寿命期内不断地改善偏差校准。这个想法是，我们可以通过环境线索推断出车辆的速度，从而形成我们的偏见估计。我们在这里很幸运，因为道路充满了专为高度可见而设计的特色。如图6所示——每束激光反射率的强度图——道路标记是激光中高度可见的特征。考虑到这些特征的重复性，以及它们往往出现在波束空间的相似区域(扫描中的角位置)，我们可以很容易地跟踪信号。

图6:沿Begbroke直线段，光束子集中的每束激光反射率随时间的变化。这张照片清楚地显示了道路中间的中间分隔栏。(浅色(蓝色)反射较弱，红色(深色)反射较强)。

图7(上)显示了图6中所示的(归一化后的)强度值的一维表示。该信号在感知带Q的生成过程中观测到。图7(下)为“经历”中点云P里，Begbroke道路中心线上的分隔栏，沿着样条模型，的归一化强度。融合这两个信号的翘曲函数就是车辆的速度。

为了提取这种翘曲函数，我们使用动态时间翘曲[13]，这是语音分析中比较音频信号的一种著名技术。给定两个信号，x∈(x1，…， xN)和y∈(y1，…，yN)，信号D(x,y)之间的失真是基于元素d（xi，yi）之间的局部距离的总和，以得到最佳匹配，使得失真最小化。这就成了一个最小化问题：

这可以用动态编程方法来解决。KΦ代表了扭曲的路径。在估计了失真后，我们可以对信号进行对齐，确定车道标记上的计时对应关系，从而推断速度。图8显示了对图6所示数据应用此过程的结果。

图8：使用所述翘曲方法，在图6所示的道路直线段上的估计速度和真实速度。地面速度真值以蓝色（实线）显示在上半图像中，估计速度以红色（虚线）显示。即使使用这些相对粗糙的标记，估计速度也会跟踪真实速度。下半图说明了在这一条带上速度估计的误差。

遗憾的是，由于目前激光的适度衰减，用这种方法来推断高曲率区域周围的速度是不可行的——跟踪会变得麻烦。目前的工作是通过进一步降低激光来解决这个问题，保持到目前为止描述的所有特性，加上允许连续的速度更新，从而消除对速度计数据的依赖。然而，就目前的情况来看，我们仅用一束推扫激光就能定量地展示出良好的定位效果。下一节将介绍这些结果。

6、结果

A.轨迹分析

为了评估定位程序的性能，我们需要一些方法来比较生成的轨迹与INS系统（惯性导航系统）的轨迹（其本身可能存在很大的误差，如图1所示）。我们将其定义为位移函数，对于姿势x（t），其定义为：

式中，Xe是测量回路中轨迹的最近姿态，如[11]中的公制测量。除了定位误差外，这种位移还将捕获从轨迹到轨迹的真实偏差。如果我们和测量车走的路线完全相同，我们希望这个位移为零。因为我们从来没有两次穿过同一条路线，所以我们期望——在一个行为良好的系统中——位移是有界的。

图9：根据Begbroke现场的经验数据测量的定位过程（红色虚线）和INS（蓝色实线）的相对偏差。在GPS信号质量差的地区，惯导系统INS显示出高的偏差。

图9描述了INS的位移（/偏差）函数和同一回路的定位程序——根据参考轨迹测量。从图中我们可以看到，INS和定位程序的位移都是有界的——但是，与INS相比，我们的方法在轨迹上的平均位移（/偏差）要低很多。INS出现较大偏差的区域（尤其是北部和南部区域）是这些区域GPS信号不足的结果。但是，我们的定位程序的位移（/偏差）在这些场所相对稳定。为了验证我们的技术，我们测试了算法在26公里的轨道数据上的性能，历时三个月。这些数据集在一天中的不同时间采集，从早上9点到晚上7点不等。

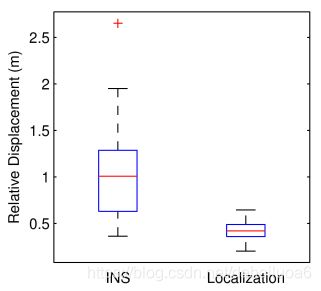
图10:从“经历”地图中得到的平均位移（/偏差）对比，一方是INS惯导系统，一方是前述我们的定位程序，超过26公里的轨迹数据、跨时三个月。箱行图显示中位数、第25和第75百分比，离群值（outliers）被单独绘制为点。从图中可以看出，我们的方法的这个位移的标准偏差要低得多。

图10显示了在此数据上收集的每个轨迹的平均位移（/偏差）的比较。所描绘的是所有所考虑的轨迹的平均位移的中位数、25%和75%。我们的方法不仅中值位移明显较低，而且消除了异常值（离群点outliers），使位移的方差大大减小。这是令人信服的证据，证明使用我们的方法进行定位在长期内比依赖于INS的估计更具可重复性。

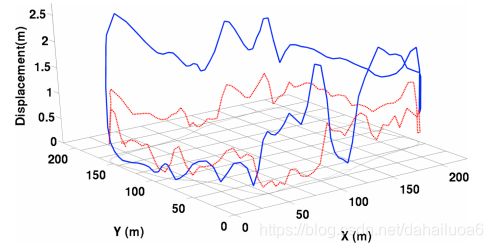
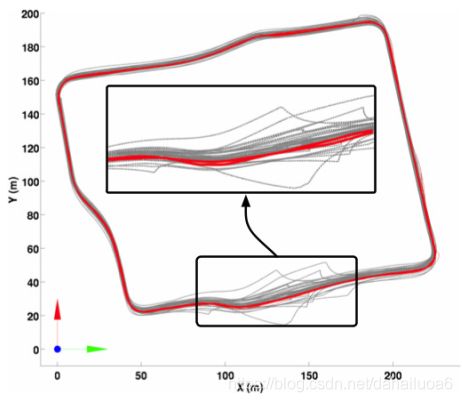
图11：原始轨迹（灰色，虚线）与校正轨迹（红色，实线）的比较。从图像中可以看出，INS数据在接收不良的区域中发生了实质性的漂移，使用所述方法可以避免这种情况（本图必须以彩色查看）。

图11对比了INS系统的轨迹（以灰色显示）和从定位程序获得的轨迹。通过观察惯性导航系统的轨迹，我们可以看到一个明显的随时间的漂移。正如预期的那样，定位程序对应的轨迹在所有数据集中更为一致，并且不会显示从INS轨迹中清晰可见的严重误差。

B.代价函数的简并性/退化（degeneracy）

KL散度（KL-divergence）通常产生具有平滑梯度的代价函数，如图12所示。然而，它也显示了混叠的效果——“走廊”问题，即图中的山谷沿着车辆的前进轨迹。

 

图12：使用感知带Q和经验地图P之间的KL散度（KL-divergence）的示例代价曲面。可看到沿车辆前进轨迹的“走廊”问题（箭头所示）。

在目前的工作中，我们正在研究如何检测（通过感知带的外观）这种简并性/退化，但在这里使用的26公里数据中，它不会导致定位失败-该问题并不重要。

7、讨论

我们再次强调了该系统在试验场地的GPS退化的南段的性能。尽管GPS集成的INS系统是目前最先进的室外导航系统，但这些系统在GPS不可用的区域无法做到长时间运行而不会发生漂移，如图11所示。使用本文中所推荐的框架模式——先验感知地图和感知带相匹配的方式（Use of a prior survey and swathe-matching using the proposed framework），无论GPS衰减如何，都可以实现稳健的长期导航。

由于试验场地是封闭的，因此在数据收集过程中，交通量相对较少。然而，停车场（位于西部和东南部）车辆数量的变化呈现出不断变化的情况，但已被恰当地处理。

虽然当前的实现方案不是实时运行的，但是生成一个实时运行的方案是毫无障碍的——滑动窗口属性需要一个初始化周期，但是算法是恒定时间的（o（1））。算法的整体复杂度由先验地图中的点的查询决定，即（作为地图大小n和所请求的点k的函数）o（√n+k）。

8、结论

总之，我们提出了一个推扫式激光定位系统，利用先验的三维测量用于道路车辆。我们在为期3个月的26公里实际数据上演示和评估了它的性能。我们相信这里的工作可以扩展到减少对角运动和线性运动率的测量的依赖。不管怎样，这个系统指导了你，离开了Velodyne品牌的产品，你还能做些什么。（怎样在不使用Velodyne产品的前提下满足激光扫描功能需求。）

9、致谢

这项工作由海军再搜索局（ONR）拨款N00140810337和EPSRC拨款EP/I005021/资助。