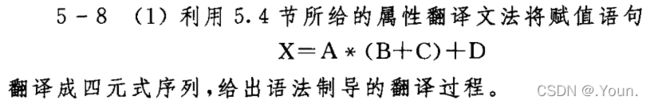编译原理笔记及例题
注：PC端观看效果最佳
注：编译原理—混子速成期末保过_哔哩哔哩_bilibili错误视频笔记（墙裂推荐）
目录
第一章 绪论
第二章 前后文无关文法和语言
第三章 词法分析及词法分析程序
第四章 语法分析及语法分析程序
第五章 语法制导的翻译及中间代码生成
第一章 绪论
1、编译系统由哪些部分组成
词法分析程序、语法分析程序、语义分析程序、中间代码生成、代码优化程序、
目标代码生成、信息表管理程序、错误检查和处理程序
第二章 前后文无关文法和语言
1、符号串
并集：A∪B = {x | x∈A or x∈B} - 注意是1个字母
乘积：AB = {xy | x∈A and y∈B} - 注意是2个字母
幂次：
= {ε}，
= 
（n>0）
正闭包：
= 
+ 
+ … + +…
自反传递闭包：A* = + + + … + +…
2、文法
文法G[S]：理解为产生式规则的集合，表示为G[S] = (
，
，P，S)
：非终结符集 ：终结符集 P：产生式集 S：开始符号
语言L(G)：由文法推导出的所有句子的集合
句型：推导过程中，由终结符和非终结符组成的字符串
句子：推导过程中，由终结符组成的字符串
3、推导和归约
自顶向下（非终结符 → 终结符）
最左推导：符号串中的最左非终结符 → 非终结符/终结符
最右推导(规范推导)：符号串中的最右非终结符 → 非终结符/终结符
自底向上（非终结符 ← 终结符）
最右归约：符号串中的最右字符 → 非终结符
最左归约(规范归约)：符号串中的最左字符 → 非终结符
4、语法树
语法树：句型推导过程对应的树形图
子树：任一结点及其全部后继（多次推导）
直接子树：子树根只有直接后继（树高为1/一次推导）
一颗语法树 = 一个最左推导/最右推导 = 多个一般推导
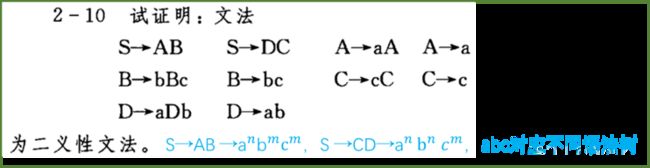
5、文法的二义性
二义性文法：L(G)文法的某个句子对应不止一个最左/最右推导/语法树
无二义性文法：L(G)文法的每一个句子都仅有一颗语法树
6、短语与句柄
短语：每颗子树的叶子（多次推导）
直接短语：每颗直接子树的叶子（一次推导）
句柄：某句型的最左直接短语（句型最左侧非终结符的直接短语）
素短语：至少包含一个终结符且不包含更小素短语的短语（短语中终结符只有一个）
《编译原理》求短语，直接短语，句柄，素短语，最左素短语 - 例题解析_肖朋伟的博客-CSDN博客_句柄和最左素短语https://blog.csdn.net/qq_40147863/article/details/93236597
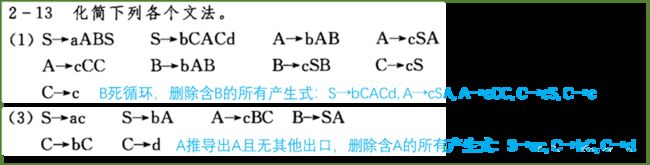
7、文法的化简
删除无用符号的产生式，删除ε-产生式(A→ε)，删除单产生式(A→B)
方法：从S开始，判断非终结符是否构成死循环（递归且不能推导到终结符串）
删除包含该非终结符的所有产生死
第三章 词法分析及词法分析程序
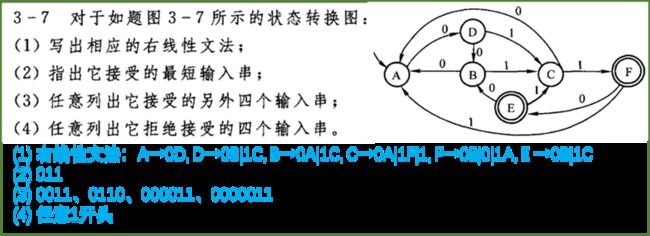
1、右线性文法、状态转换图（文法→DFA）
右线性文法：仅有形如A→αB及A→α的产生式
状态转换图（右线性文法，无ε产生式）：
A→aB：
A→a：
解题：文法 → 语法树 → 句子形式 → 状态转换图 → 读出右线性文法
3型文法 = 正规文法 → 右线性文法/左线性文法
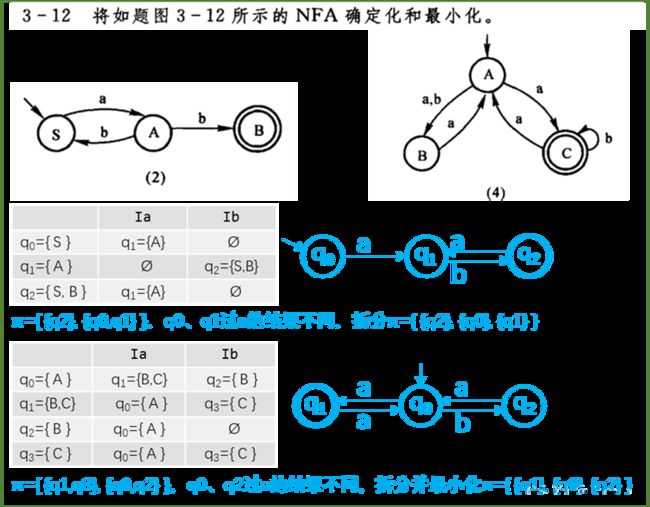
2、确定化和最小化
确定有限自动机（NFA）：初态有一个，输入有唯一确定的转移状态
不确定有限自动机（DFA）：初态有多个，对于同一输入有多个转移状态
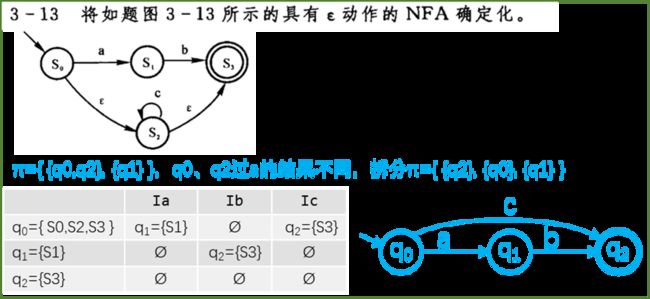
确定化（NFA → DFA）：
①确定新初态 q0 = ε-closure(S)
从初态S出发，经任意条ε线所能到达的状态组成新初态
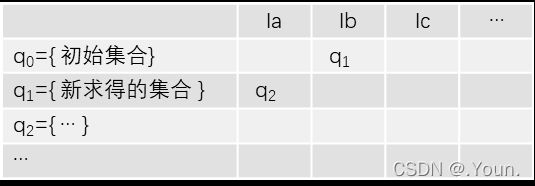
②造表
/ 
/ 
：从q出发，经一条a/b/c实线和任意条ε线所到达的状态集
③得到DFA 新终态为包含原终态的所有状态集
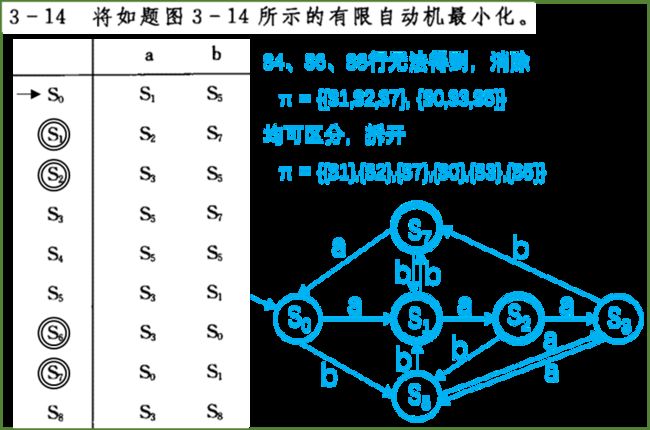
最小化（DFA）：
①初始化 π={ {终态集}，{其它集合} }
②对每个集合进行划分，直到集合中状态无法区分
集合中所有状态经同种实线到达相同的集合
③每个集合仅保留一个状态
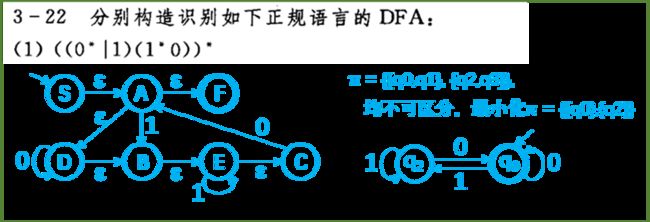
3、正规式与有限自动机（单词→DFA）
正规式：将文法的终结符号用 *、· 、| 连接组成的表达式，表示单词集
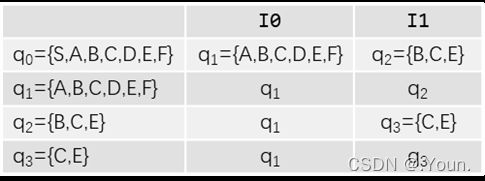
由正规式构造有限自动机（分裂法）：
①正规语言→NFA：
②确定化和最小化
第四章 语法分析及语法分析程序
0、概述
自顶向下的语法分析
LL(1)分析、递归下降分析、预测分析
自底向上的语法分析
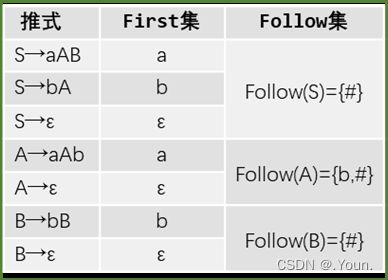
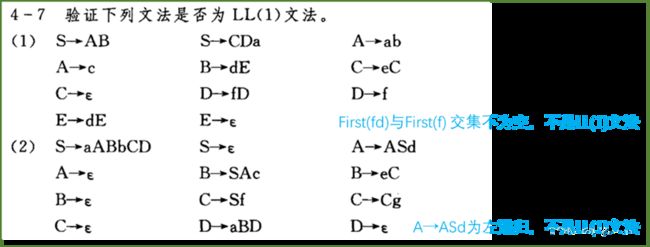
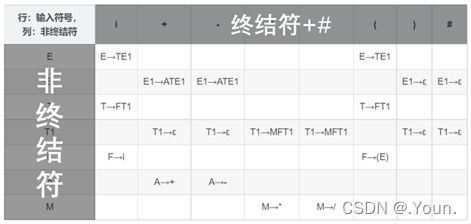
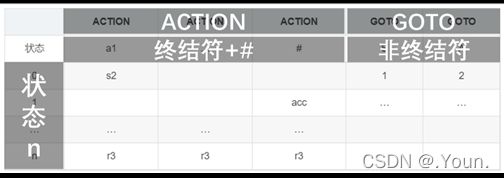
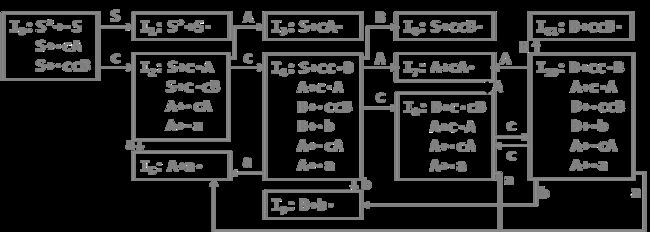
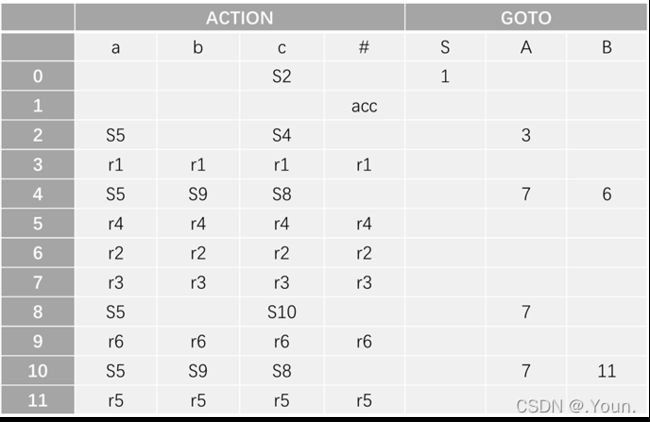
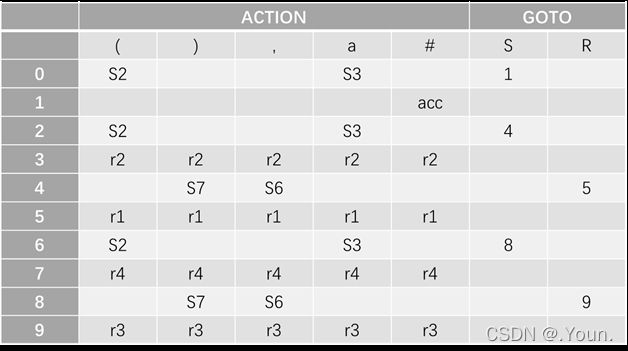
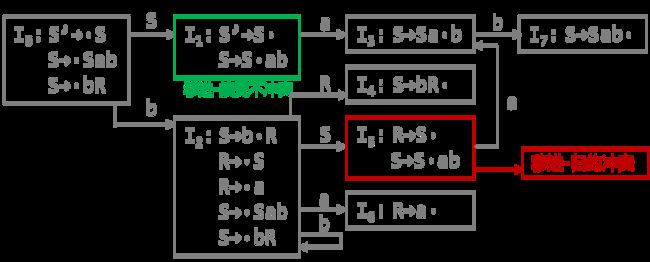
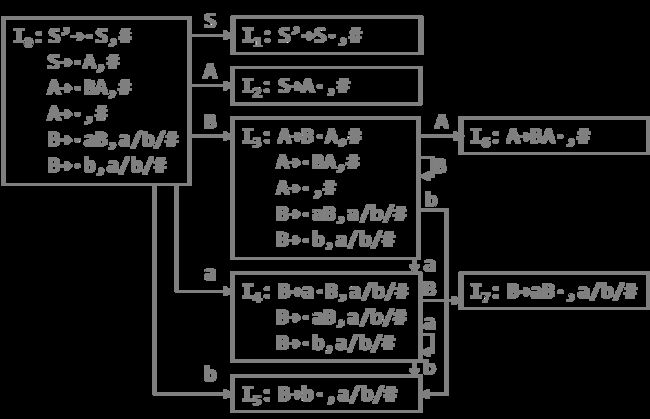
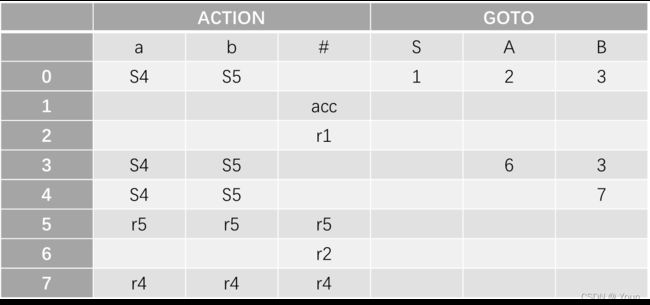
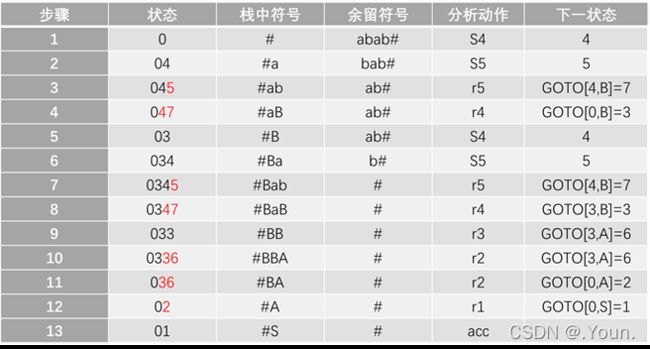
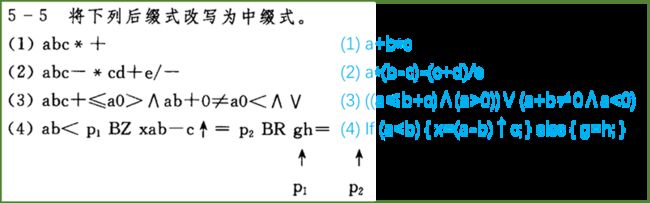
简单优先、算符优先、优先函数、LR分析 LR(0) 1、消除左递归性 将A→Aα|β 改写为 A→βA’，A’→αA’|ε （推导结果相同） 2、First(X)集 由X能推导出的句型中，以终结符开头的该终结符所组成的集合 ①X是终结符，First(X) = {X} 终结符本身 ②X是非终结符，若X→a…，则a∈First(X)；若X→ε，则 ε∈First(X) ③X→Y1Y2…Yk 非终结符能推出ε，加上它的Follow集 Y1是非终结符，First(Y1)-{ε} ∈ First(X) Y1,…Yi为非终结符且能推出ε，则First(Y1)…First(Yi+1)中一切非ε∈First(X) Y1、Y2、…Yk都能推导出ε，则ε∈First(X) 3、Follow(A)集 由开始符号推导出的句型中，位于非终结符A后的终结符组成的集合 ①开始符S，#∈Follow(S) 开始符号为 # ②B→αAβ，First(β)-{ε}∈Follow(A) A后字符的First集 ③B→αAβ且ε∈First(β)，则Follow(B)∈Follow(A) A为最右字符，加上B的Follow集 4、判断LL(1)文法（基于产生式） ①文法不含左递归 ②对G中每个产生式A→B1|B2|…Bm,其各项候选式均满足：（两两不相交） First(Bi) ∩ First(Bj) = Ø 若有候选式Bi为ε，则First(Bj) ∩ Follow(A)=Ø ( Follow(A)∈First(Bi) ) 5、LL(1)分析表 对于A→Bi： ①若First(Bi)=a，则M[A, a]处填入此产生式 （First集） ②若First(Bi)=ε，则求Follow(A)=b，M[A, b]处填入此产生式 （First集） ③其余空着error 6、LL(1)分析过程 - 最右推导 #S入栈，读取待匹配字符，用对应产生式右侧替换栈顶（入栈后读取时逆序） 当栈顶元素与待匹配字符相同时，弹出，进行下一个字符的匹配 匹配结果要么为error（失败），要么为#（成功） 7、LR(0)项目 产生式右部某位置上标有 · 的产生式，表示当前分析位置 移进项目（A→α·xβ）x为终结符 待约项目（A→α·Xβ）X为非终结符 归约项目（A→α· ） 非开始符号A 接受项目（S→α· ）开始符号S 8、项目集闭包 等价项目的集和，每个项目集闭包对应自动机的一个状态 方法：求基本项目集I，对I中待约项目A→α·Bβ，加入B的所有初始项目B→·γ 9、判断LR(0)文法（基于项目集闭包） 无冲突项目（移进-归约、归约-归约冲突） 10、LR(0)分析表 ACTION： S1：表示当前状态集为移进项目，经终结符a变为状态集1 r1：表示当前状态集为归约项目，对应产生式序号1（ACTION内此行都填r1） acc：表示当前状态集为接受项目，在#处填acc GOTO：n：表示当前状态集经过此非终结符到达的状态集n 11、LR(0)分析法 - 最左归约 将符号串逐个移进栈，当形成可规约子串时，替换为非终结符， 循环直到字符串全部接收且栈中为开始符号S (1) 拓广文法： 增加S’→S产生式，保证开始符号只在左式出现一次 ⓪S’→S，①S→cA，②S→ccB，③A→cA，④A→a，⑤B→ccB，⑥B→b (2) 识别全部活前缀的DFA： (3) 项目集规范族：{I0, I1, I2, I3, I4, I5, I6, I7, I8, I9, I10, I11} (4) LR(0)分析表 (1) 拓广文法： ⓪S’→S ①S→(SR ②S→a ③R→,SR ④R→) (2) 识别全部活前缀的DFA：… DFA中无冲突，是LR(0)文法，也是SLR(1),LR(1),LALR(1) (3) 项目集规范族：{I0, I1, I2, I3, I4, I5, I6, I7, I8, I9 } (4) LR(0)分析表： 12、判断SLR(1)文法 ①DFA中存在冲突项目（移进-归约、归约-归约冲突） ②每个冲突项目集In={A1→α·a1β, A2→α·a2β…, B1→α·, B2→α·,…} (两两不相交) 当{a1、a2…}、FOLLOW(B1)、FOLLOW(B2)…两两不相交时为SLR(1)文法 13、SLR(1)分析表 对于每个归约项目A→α·,求FOLLOW(A)得到的符号处填r n(非整行,n为产生式序号) 其余同LR(0)分析表一样 (1) 拓广文法： ⓪S’→S ①S→Sab ②S→bR ③R→S ④R→a (2) 识别全部活前缀的DFA： (3) I5移进-归约冲突，而{a}、FOLLOW{R}={a,#}相交，不是SLR(1)文法 (1) 拓广文法： ⓪S’→S ①S→aSb ②S→bSa ③S→ab (2) 识别全部活前缀的DFA：… (3) I5移进-归约冲突,而{a,b}、FOLLOW{S}={a,b,#}相交，不是SLR(1)文法 14、判断LR(1)文法 构造带向前搜索符的DFA 无归约-归约冲突 (具有不同向前搜索符的同一产生式不冲突) 15、LR(1)文法DFA In中，每一个项目都形如 A→α·β,a 对于A→α·Bβ,a的等价项目B→·γ,b： b=First(βa)：当β=ε时，b=a；当β≠ε时，b=First(β) 16、LR(1)分析表 每个状态In中，若存在归约项目，其r n根据向前搜索符填写 (在归约项目的所有向前搜索符的对应位置填写r n) (项目的·移动时向前搜索符不变，但新增的等价项目要重新计算向前搜索符) (1) 拓广文法： ⓪S’→S ①S→A ②A→BA ③A→ε ④B→aB ⑤B→b (2) 识别全部活前缀的DFA： (3) 无归约-归约冲突，是LR(1)文法 (4) LR(1)分析表 *(5) 分析过程： 归约时弹出几个元素，指针前移几位，求得新状态后入栈 GOTO[状态栈指针所指状态，归约产生式左侧元素]=下一状态 (1) 判断LL(1) First(AaAb)={a} ∩ First(BbBa)={b} = ∅，是LL(1)文法 (2) 判断SLR(1) ①拓广文法： ⓪S’→S ①S→AaAb ②S→BbBa ③A→ε ④B→ε ②识别全部活前缀的DFA： ③冲突项目集I0中，FOLLOW(A)={a,b}∩FOLLOW(B)={a,b}≠∅，不是SLR(1)文法 17、判断LALR(1)文法 合并同心集后无归约-归约冲突 (合并为一个项目集，相同产生式的搜索符合并) 同心集：两个项目集闭包的所有产生式均相同，只有向前搜索符不同 0、LR(0) 1、⓪S’→S，①S→Aa ②S→bAc ③S→dc ④S→bda ⑤A→d 合并同心集后没有归约-归约冲突，是LALR(1)文法 冲突项目集I4中，{c}∩FOLLOW(A)={a,c}≠∅，不是SLR(1)文法 2、⓪S’→S，①S→Aa ②S→bAc ③S→Bc ④S→bBa ⑤A→d ⑥B→d 没有归约-归约冲突，是LR(1)文法（向前搜索符不同） 合并同心集I5、I10后有归约-归约冲突，不是LALR(1)文法 1、逆波兰式(后缀表达式) 运算对象顺序相同，运算符紧跟其运算对象后 转移操作符： p BR：(branch)无条件转移到p e’ p BZ：(branch zero)e’为假时转移到p(e’为e的后缀表达式) e1’ e2’ p BL: (branch less)当e1’ 2、各类运算符优先级（由高到低） 括号 算术运算符 *、/ > +、- 关系运算符 <、<=、=、>、>=、<> 逻辑运算符 非>与>或 字母入栈，遇到运算符时弹出字母进行运算，结果再入栈 3、四元式 (操作符，左操作数，右操作数，结果) (+,B,C,T1), (*,A,T1,T2), (+,T2,D,T3), (=,T3,-,X) 4、布尔表达式→四元式序列 ①（jnz,A1,-,p）:当A1为真时，跳向p四元式 ②（jrop,A1,A2,p）:当A1 rop A2成立时，跳向p ③（j,-,-,p）：无条件跳向p A∧B：A为假则假 A∨B：A为真则真 ┐A：A真则假，A假则 5、 DAG 图与求优化后的 4 元式 《编译原理》画 DAG 图与求优化后的 4 元式代码- 例题解析_肖朋伟的博客-CSDN博客_四元式划分基本块
画出表格
第五章 语法制导的翻译及中间代码生成
https://blog.csdn.net/qq_40147863/article/details/93376991