Graph Neural Networks (GNN)（三）：Spectral-GNN 之 GCN

1. 概述

前面讲了 Spectral-GNN Graph Neural Networks (GNN)（二）：Spectral-GNN 引言和导入 的引言和导入。这一篇主要介绍这一类最经典的一条模型主线：GCN。
参考链接：
如何理解 Graph Convolutional Network（GCN）？-- Johnny Richards 的回答
如何理解 Graph Convolutional Network（GCN）？-- superbrother 的回答

2. 离散卷积

了解 GCN 之前必须对离散卷积（或者说 CNN 中的卷积）有一个明确的认识：离散卷积本质就是一种加权求和。

CNN 中的卷积本质就是利用一个共享参数的过滤器（filter），通过计算中心像素点以及相邻像素点的加权和来构成 feature map 实现空间特征的提取，当然加权和系数就是卷积核的权重系数。那么卷积核的系数如何确定的呢？是随机化初值，然后根据误差函数通过反向传播梯度下降进行迭代优化。这是一个关键点，卷积核的参数通过优化才能实现特征提取的作用，GCN 的理论很大一部分工作就是为了引入可以优化的卷积参数。

这里提一句：这里的卷积是指深度学习（CNN）中的卷积，与数学中定义的卷积运算严格意义上是有区别的。最直观的就是：是否进行翻转，然后再进行对应元素的加权求和。

• 数学中卷积，主要是为了诸如信号处理、求两个随机变量和的分布等而定义的运算，所以需要“翻转”是根据问题的需要而确定的。
• 卷积神经网络中“卷积”，是为了提取图像的特征，其实只借鉴了“加权求和”的特点。
• 还有一点一定要说的是：数学中的“卷积核”都是已知的或者给定的，卷积神经网络中“卷积核”本来就是 trainable 的参数，不是给定的，根据数据训练学习的，那么翻不翻转还有什么关系呢？因为无论翻转与否对应的都是未知参数！

3. Why GCN？

CNN处理的图像或者视频数据中像素点（pixel）是排列成成很整齐的矩阵（也就是很多论文中所提到的Euclidean Structure），与之相对应，科学研究中还有很多 Non Euclidean Structure 的数据，如社交网络、信息网络等。

为什么要研究 GCN 呢？

1. CNN 无法处理 Non Euclidean Structure 的数据，学术上的表达是传统的离散卷积在 Non Euclidean Structure 的数据上无法保持平移不变性。通俗理解就是在拓扑图中每个顶点的相邻顶点数目都可能不同，那么当然无法用一个同样尺寸的卷积核来进行卷积运算。
2. 由于 CNN 无法处理 Non Euclidean Structure 的数据，又希望在这样的数据结构（拓扑图）上有效地提取空间特征来进行机器学习，所以 GCN 成为了研究的重点。

4. 不同解决方案

GCN 的本质目的就是用来提取拓扑图的空间特征，那么实现这个目标只有这一种途径吗？当然不是，在vertex domain (spatial domain) 和 spectral domain 实现目标是两种最主流的方式。

vertex domain (spatial domain)是非常直观的一种方式。就是聚合邻居节点的信息来更新本节点的特征，具体的实现可以参考本系列第一篇论文 Spatial-GNN Graph Neural Networks (GNN)（一）：Spatial - GNN 。

spectral domain 就是 GCN 的理论基础了。这种思路就是希望借助图谱的理论来实现拓扑图上的卷积操作。从整个研究的时间进程来看：首先研究 GSP（graph signal processing）的学者定义了 graph 上的Fourier Transformation，进而定义了 graph 上的 convolution，最后与深度学习结合提出了Graph Convolutional Network。

5. GCN

上面讲到 GCN 就是借助图谱理论来实现拓扑图上的卷积操作。

5.1 什么是图谱理论（Spectral Graph Theory）

Spectral Graph Theory 可以参考 wiki 百科 Spectral Graph Theory，简单的概括就是借助于图的拉普拉斯矩阵的特征值和特征向量来研究图的性质。

5.2 Why Spectral Graph Theory

这个可以参考上一篇论文，拉普拉斯矩阵的作用和原理。Graph Neural Networks (GNN)（二）：Spectral-GNN 引言和导入。

5.3 拉普拉斯矩阵

对于图 $G=(V,E)$，其 Laplacian 矩阵的定义为 $L=D-A$，其中 $L$ 是拉普拉斯矩阵，$D$ 是顶点的度矩阵（一个对角矩阵），对角线元素依次为各顶点的度，$A$ 是图的邻接矩阵。

这里要说明的是：常用的拉普拉斯矩阵实际有三种：

1. $L=D-A$ 定义的拉普拉斯矩阵的专业名称叫做 Combinatorial Laplacian。
2. $L^{sys}=D^{-1/2}L{D}^{-1/2}$ 定义的叫做 Symmetric normalized Laplacian。很多 GCN 的论文中应用的是这种拉普拉斯矩阵。
3. $L^{rw}=D^{-1}L$ 定义的叫 Random walk normalized Laplacian

拉普拉斯矩阵矩阵有很多良好的性质：

1.拉普拉斯矩阵是对称矩阵，可以进行特征分解（谱分解），这就和 GCN 的 spectral domain 对应上了。
2. 拉普拉斯矩阵只在中心顶点和一阶相连的顶点上（1-hop neighbor）有非 0 元素，其余之处均为 0。
3. 通过拉普拉斯算子与拉普拉斯矩阵进行类比。图拉普拉斯矩阵，如果把它看作线性变换的话，它起的作用与数学分析中的拉普拉斯算子是一样的。也就是说拉普拉斯矩阵就是图上的拉普拉斯算子，或者说是离散的拉普拉斯算子。

5.4 拉普拉斯矩阵的谱分解

GCN 的核心基于拉普拉斯矩阵的谱分解，文献中对于这部分内容没有讲解太多，初学者可能会遇到不少误区，所以先了解一下特征分解。

矩阵的谱分解，特征分解，对角化都是同一个概念。

不是所有的矩阵都可以特征分解，其充要条件为 n 阶方阵存在 n 个线性无关的特征向量。但是拉普拉斯矩阵是半正定对称矩阵，（半正定矩阵本身就是对称矩阵，此处这样写为了和下面的性质对应，避免混淆），有如下三个性质：

1. 对称矩阵一定n个线性无关的特征向量。
2. 半正定矩阵的特征值一定非负。
3. 对阵矩阵的特征向量相互正交，即所有特征向量构成的矩阵为正交矩阵。

由上可以知道拉普拉斯矩阵一定可以谱分解，且分解后有特殊的形式。对于拉普拉斯矩阵的谱分解为：

$L=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)U^{-1}$

其中 $U=(u_1,u_2,\cdots ,u_n)$ 是列向量为单位特征向量的矩阵，其中 $u_l$ 是列向量。$\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)$ 是 n 个特征值构成的对角矩阵。其中 $U$ 是正交矩阵，即 $U{U}^T=E$。所以特征分解也可写成：

$L=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)U^{-1}=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)U^T$

文献中都是最后导出的这个公式，但大家不要误解，特征分解最右边的是特征矩阵的逆，只是拉普拉斯矩阵的性质才可以写成特征矩阵的转置。

5.5 如何从传统的傅里叶变换、卷积类比到 Graph 上的傅里叶变换及卷积？

把传统的傅里叶变换以及卷积迁移到 Graph 上来，核心工作其实就是把拉普拉斯算子的特征函数 $e^{-i\omega t}$ 变为 Graph 对应的拉普拉斯矩阵的特征向量。

传统的傅里叶变换定义为：$F(\omega )=\mathcal{F}[f(t)]=\int f(t)e^{-i\omega t}dt$，信号 $f(t)$ 与基函数 $e^{-i\omega t}$ 的积分。那么为什么用 $e^{-i\omega t}$ 作为基函数呢？ 数学上看，$e^{-i\omega t}$ 是拉普拉斯算子的特征函数（满足特征方程），$\omega$ 就和特征值有关。

广义的特征方程：$AV=\lambda V$，其中 $A$ 是一种变换，$V$ 是特征向量或者特征函数，$\lambda$ 是特征值。$e^{-i\omega t}$ 满足 $\Delta e^{-i\omega t}=\frac{{\partial }^2}{\partial t^2}{e}^{-i\omega t}=-{\omega }^2{e}^{-i\omega t}$，当然 $e^{-i\omega t}$ 就是变换 $\Delta$ 的特征函数，$\omega$ 就和特征值密切相关。

处理 Graph 问题的时候，用到拉普拉斯矩阵（拉普拉斯矩阵就是离散拉普拉斯算子），自然就去找拉普拉斯矩阵的特征向量了。$L$ 是拉普拉斯矩阵， $V$ 是其特征向量，自然满足: $LV=\lambda V$。

离散卷积就是一种内积形式：$F\left({\lambda }_l\right)=\hat{f}\left({\lambda }_l\right)={\sum }_{i=1}^{N}f(i)u_l^{\ast }(i)$，$f$ 是 Graph 上的 N 维向量，$f(i)$ 与 Graph 的顶点一一对应，$v_l(i)$ 表示第 $l$ 个特征向量的第 $i$ 个分量。那么特征值（频率）${\lambda }_l$ 下的 $f$ 的 Graph 傅里叶变换就是与 ${\lambda }_l$ 对应的特征向量 $u_l$ 进行内积运算。上述的内积运算是在复数空间中定义的，所以采用了 $u_l^{\ast }(i)$，也就是特征向量 $u_l$ 的共轭。

利用卷积乘法将 Graph 上的傅里叶变换推广到卷积形式：
$\left(\begin{array}{c}\hat{f}\left({\lambda }_1\right)\\ \hat{f}\left({\lambda }_2\right)\\ ⋮\\ \hat{f}\left({\lambda }_N\right)\end{array}\right)=\left(\begin{array}{cccc}{u}_1(1)& u_1(2)& \dots & u_1(N)\\ u_2(1)& u_2(2)& \dots & u_2(N)\\ ⋮& ⋮& \ddots & ⋮\\ u_N(1)& u_N(2)& \dots & u_N(N)\end{array}\right)\left(\begin{array}{c}f(1)\\ f(2)\\ ⋮\\ f(N)\end{array}\right)$
即 $f$ 在 Graph 傅里叶变换的矩阵形式为：

$\hat{f}=U^{T}f$

Graph 上的傅里叶逆变换: 类似的传统的傅里叶逆变换是对频率 $\omega$ 求积分：${\mathcal{F}}^{-1}[F(\omega )]=\frac{1}{2\Pi }\int F(\omega )e^{i\omega t}d\omega$，迁移到 Graph 上变为对特征值 ${\lambda }_l$ 求和：$f(i)={\sum }_{l=1}^N\hat{f}\left({\lambda }_l\right)u_l(i)$，利用矩阵乘法将Graph上的傅里叶逆变换推广到矩阵形式：
$\left(\begin{array}{c}f(1)\\ f(2)\\ ⋮\\ f(N)\end{array}\right)=\left(\begin{array}{cccc}{u}_1(1)& u_2(1)& \dots & u_N(1)\\ u_1(2)& u_2(2)& \dots & u_N(2)\\ ⋮& ⋮& \ddots & ⋮\\ u_1(N)& u_2(N)& \dots & u_N(N)\end{array}\right)\left(\begin{array}{c}\hat{f}\left({\lambda }_1\right)\\ \hat{f}\left({\lambda }_2\right)\\ ⋮\\ \hat{f}\left({\lambda }_N\right)\end{array}\right)$
即 $f$ 在 Graph 傅里叶逆变换的矩阵形式为：

$f=U\hat{f}$

在上面的基础上，利用卷积定理类比来将卷积运算，推广到 Graph 上。

卷积定理：函数卷积的傅里叶变换是函数傅立叶变换的乘积，即对于函数 $f(t)$ 与 $h(t)$ 两者的卷积就是其函数傅立叶变换乘积的逆变换。

$f\ast h={\mathcal{F}}^{-1}[\hat{f}(\omega )\hat{h}(\omega )]=\frac{1}{2\Pi }\int \hat{f}(\omega )\hat{h}(\omega )e^{i\omega t}d\omega$

类比到 Graph 上并把傅里叶变换的定义带入， $f$ 与卷积核 $h$ 在 Graph 上的卷积可按照下列步骤求出：

1. $f$ 的傅里叶变换为：$\hat{f}=U^{T}f$。
2. 卷积核 $h$ 的傅里叶变换写成对角矩阵的形式就是：$\left(\begin{array}{ccc}\hat{h}\left({\lambda }_1\right)& & \\ & \ddots & \\ & & \hat{h}\left({\lambda }_n\right)\end{array}\right)$，$\hat{h}\left({\lambda }_l\right)={\sum }_{i=1}^{N}h(i)u_l^{\ast }(i)$，是根据需要设计的卷积核 $h$ 在 Graph 上的傅里叶变换。
3. 两者的傅立叶变换乘积即为：$\left(\begin{array}{ccc}\hat{h}\left({\lambda }_1\right)& & \\ & \ddots & \\ & & \hat{h}\left({\lambda }_n\right)\end{array}\right)U^{T}f$
4. 再乘以 $U$ 求两者傅立叶变换乘积的逆变换，则求出卷积：$(f\ast h{)}_G=U\left(\begin{array}{ccc}\hat{h}\left({\lambda }_1\right)& & \\ & \ddots & \\ & & \hat{h}\left({\lambda }_n\right)\end{array}\right)U^{T}f$

注：很多论文中的Graph卷积公式为：$(f\ast h{)}_G=U\left(\left(U^{T}h\right)\odot \left(U^{T}f\right)\right)$，其中 $\odot$ 表示 Hadamard product（哈达马积），对于两个维度相同的向量、矩阵、张量进行对应位置的逐元素乘积运算。其实两者是完全等价的。

5.6 为什么拉普拉斯矩阵的特征向量可以作为傅里叶变换的基？特征值表示频率？

5.6.1 为什么拉普拉斯矩阵的特征向量可以作为傅里叶变换的基？

傅里叶变换一个本质理解就是：把任意一个函数表示成了若干个正交函数（由 sin, cos 构成）的线性组合。 通过上一节中的公式 $f=U\hat{f}$ 看出 graph傅里叶变换也把graph 上定义的任意向量 $f$ 表示成了拉普拉斯矩阵特征向量的线性组合，即：$f=\hat{f}\left({\lambda }_1\right)u_1+\hat{f}\left({\lambda }_2\right)u_2+\cdots +\hat{f}\left({\lambda }_n\right)u_n$。那么：为什么 graph 上任意的向量 $f$ 都可以表示成这样的线性组合？原因在于 $(u_1,u_2,\cdots ,u_n)$ 是 graph 上 $n$ 维空间中的 $n$ 个线性无关的正交向量，由线性代数的知识可以知道：$n$ 维空间中 $n$ 个线性无关的向量可以构成空间的一组基，而且拉普拉斯矩阵的特征向量还是一组正交基。

5.6.2 怎么理解拉普拉斯矩阵的特征值表示频率？

在 graph 空间上无法可视化展示“频率”这个概念，那么从特征方程上来抽象理解。将拉普拉斯矩阵 $L$ 的 $n$ 个非负特征向量，从小到大排列为 ${\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_n$，而且最小的特征值 ${\lambda }_1=0$，因为 $n$ 维的全 1 向量的特征值为 0（由 $L$ 的定义可以得出）：$L\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right)=0$。
从特征方程的数学理解来看：$Lu=\lambda u$，在由Graph确定的 $n$ 维空间中，越小的特征值 ${\lambda }_l$ 表明：拉普拉斯矩阵 $L$ 其所对应的基 $u_l$ 上的分量、“信息”越少，那么当然就是可以忽略的低频部分了。

其实图像压缩就是这个原理，把像素矩阵特征分解后，把小的特征值（低频部分）全部变成 0；PCA 降维也是同样的，把协方差矩阵特征分解后，按从大到小取出前K个特征值对应的特征向量作为新的“坐标轴”。

6. Deep Learning中的Graph Convolution

Deep learning 中的 Graph Convolution 直接看上去会和上面推导出的图卷积公式有很大的不同，但是万变不离其宗，推导的本源是：

$(f\ast h{)}_G=U\left(\begin{array}{ccc}\hat{h}\left({\lambda }_1\right)& & \\ & \ddots & \\ & & \hat{h}\left({\lambda }_n\right)\end{array}\right)U^{T}f$

本篇博客最开始已经解释得很清楚：Deep learning 中的 Convolution 就是要设计含有 trainable 共享参数的 kernel，从上式看很直观：graph convolution 中的卷积参数就是 $\mathrm{diag}\left(\hat{h}\left({\lambda }_l\right)\right)$

6.1 第一代 GCN

Spectral Networks and Locally Connected Networks on Graphs 中简单粗暴地把 $\mathrm{diag}\left(\hat{h}\left({\lambda }_l\right)\right)$ 变成了卷积核 $\mathrm{diag}\left({\theta }_l\right)$，也就是：

$y_{\text{output}}=\sigma \left(U{g}_{\theta }(\Lambda )U^{T}x\right)$。

（为避免混淆，本文中称 $g_{\theta }(\Lambda )$ 是卷积核， $U{g}_{\theta }(\Lambda )U^T$ 的运算结果为卷积运算矩阵）。

$g_{\theta }(\Lambda )=\left(\begin{array}{ccc}{\theta }_1& & \\ & \ddots & \\ & & {\theta }_n\end{array}\right)$

这就是标准的第一代 GCN 中的 layer 了，其中 $\sigma (\cdot )$ 是激活函数，$\Theta =\left({\theta }_1,{\theta }_2,\cdots ,{\theta }_n\right)$ 就跟神经网络中的 weight 一样是任意的参数，通过初始化赋值然后利用误差反向传播进行调整，$x$ 就是 graph 上对应于每个顶点的 feature vector（由特数据集提取特征构成的向量）。

第一代的参数方法存在着一些弊端：主要在于：

1. 每一次前向传播，都要计算 $U,\mathrm{diag}\left({\theta }_l\right)$ 及 $U^T$ 三者的矩阵乘积，特别是对于大规模的 graph，计算的代价较高，也就是论文中 $\mathcal{O}\left(n^2\right)$ 的计算复杂度。
2. 卷积核不具有 spatial localization。
3. 卷积核需要 $n$ 个参数。

6.2 第二代 GCN

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering 把 $\hat{h}\left({\lambda }_l\right)$ 巧妙地设计成了 ${\sum }_{i=0}^K{\alpha }_j{\lambda }_l^j$，也就是：

$y_{\text{output}}=\sigma \left(U{g}_{\theta }(\Lambda )U^{T}x\right)$
$g_{\theta }(\Lambda )=\left(\begin{array}{ccc}{\sum }_{j=0}^K{\alpha }_j{\lambda }_1^j& & \\ & \ddots & \\ & & {\sum }_{j=0}^K{\alpha }_j{\lambda }_n^j\end{array}\right)$

上面的公式仿佛还什么都看不出来，下面利用矩阵乘法进行变换，来一探究竟。

$\left(\begin{array}{ccc}{\sum }_{j=0}^K{\alpha }_j{\lambda }_1^j& & \\ & \ddots & \\ & & {\sum }_{j=0}^K{\alpha }_j{\lambda }_n^j\end{array}\right)={\sum }_{j=0}^K{\alpha }_j{\Lambda }^j$

进而推导出：

$U{\sum }_{j=0}^K{\alpha }_j{\Lambda }^j{U}^T={\sum }_{j=0}^K{\alpha }_{j}U{\Lambda }^j{U}^T={\sum }_{j=0}^K{\alpha }_j{L}^j$

其中：$L^2=U\Lambda U^{T}U\Lambda U^T=U{\Lambda }^2{U}^T$ 且 $U^{T}U=E$

于是：$y_{\text{output}}=\sigma \left({\sum }_{j=0}^{K-1}{\alpha }_j{L}^{j}x\right)$ 其中 $\left({\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_{K-1}\right)$ 是任意的参数，通过初始化赋值然后利用误差反向传播进行调整。

这样设计的卷积核的好处：

1. 卷积核只有 $K$ 个参数，一般 $K$ 远小于 $n$，参数的复杂度被大大降低了。
2. 矩阵变换后，神奇地发现不需要做特征分解了，直接用拉普拉斯矩阵 $L$ 进行变换。然而由于要计算$L^j$，计算复杂度还是 $\mathcal{O}\left(n^2\right)$。
3. 卷积核具有很好的spatial localization，特别地， $K$ 就是卷积核的 receptive field，也就是说每次卷积会将中心顶点 K-hop neighbor 上的 feature 进行加权求和，权系数就是 ${\alpha }_k$。

更直观的：$K=1$ 就是对每个顶点上一阶 neighbor 的 feature 进行加权求和，如下图所示：
同理，$K=2$ 的情形如下所示：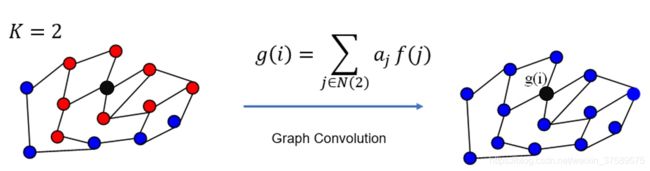
注：上图只是以一个顶点作为实例，GCN 每一次卷积对所有的顶点都完成了图示的操作。

这里是不是发现和 Spatial GNN 很相似啊，是的。其实所有 GNN 本质都是一样的，只是出发点不同，最后殊途同归。

6.3 Chebyshev GCN

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering 利用Chebyshev多项式代替卷积核，就可以得到下式：

$g_{\theta }(\Lambda )={\sum }_{k=0}^{K-1}{\beta }_k{T}_k(\tilde{\Lambda })$

其中， $T_k(\cdot )$ 是 $k$ 阶的 Chebyshev 多项式， ${\beta }_k$ 是对应的系数 $($ 也就是训续中迭代更新的参数)。 $\tilde{\Lambda }$ 是 re-scaled 的特征值对角矩阵, 进行这个 shift 变换的原因是Chebyshev 多项式的输入要在 [-1,1] 之间，具体操作是：$\tilde{\Lambda }=2\Lambda /{\lambda }_{\max }-I$，${\lambda }_{max}$ 是最大的特征值。最后得到的 GCN 层就是：

$y=\sigma \left({\sum }_{k=0}^{K-1}{\beta }_k{T}_k\left(U\tilde{\Lambda }{U}^T\right)x\right)$

因为 $L=U\Lambda U^T$，代入可以得：

$y=\sigma \left({\sum }_{k=0}^{K-1}{\beta }_k{T}_k(\tilde{L})x\right)$

其中， $\tilde{L}=2L/{\lambda }_{max}-I$ 。这样变换的好处在于：计算过程无需再进行特征向量分解。

在实际运算过程中，可以利用 Chebyshev 多项式的性质，进行递推：

$T_k(\tilde{L})=2\tilde{L}{T}_{k-1}(\tilde{L})-T_{k-2}(\tilde{L})$
$T_0(\tilde{L})=I,T_1(\tilde{L})=\tilde{L}$

这样 filter 操作的复杂度为：$\mathcal{O}(K|\mathcal{E}|)\ll \mathcal{O}\left(n^2\right)$，其中 $|\mathcal{E}|$ 是边数。

6.4 经典 GCN

Semi-Supervised Classification with Graph Convolutional Networks 进一步简化：$K=1$

$\begin{array}{rl}y& \approx \sum _{k=0}^1{\theta }_k^{\prime }{T}_k(\tilde{L})\mathbf{x}\\ & ={\theta }_0^{\prime }\mathbf{x}+{\theta }_1^{\prime }(\mathbf{L}-\mathbf{I})\mathbf{x}\\ & ={\theta }_0^{\prime }\mathbf{x}-{\theta }_1^{\prime }{\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}\mathbf{x}\end{array}$

因为 $\theta$ 是个filter 的 parameter, 所以可以 $\theta ={\theta }_0^{\prime }=-{\theta }_1^{\prime }$ 那 么这个时候就变成了

$y\approx \theta \left(\mathbf{I}+{\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}\right)\mathbf{x}$

作者表示 $\mathbf{I}+{\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}$ 的特征值范围为 [0, 2]，重复多次使用这个操作算子会导致数值不稳定，因此作者使用了一种 renormalization trick：

$I+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$

其中 $\tilde{A}=A+I_N$ 以及 ${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$，因此最后的经典 GCN 就是：

$y\approx \theta \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}\right)\mathbf{x}$

令 $\hat{A}={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$，一个两层的经典 GCN 就是：

$Z=f(X,A)=\mathrm{softmax}\left(\hat{A}\mathrm{ReLU}\left(\hat{A}X{W}^{(0)}\right)W^{(1)}\right)$

$X\in {\mathbb{R}}^{N\times C}$ 表明每个节点特征维度为 $C$，然后参数 $W\in {\mathbb{R}}^{C\times F}$，边数为 $|\mathcal{E}|$，filter 算子的复杂度为：$\mathcal{O}(|\mathcal{E}|FC)$。

7. 在 GCN 中的 Local Connectivity 和 Parameter Sharing

CNN中有两大核心思想：网络局部连接，卷积核参数共享。那么我们不禁会联想：这两点在 GCN 中是怎样的呢？以下图的 graph 结构为例来探究一下。

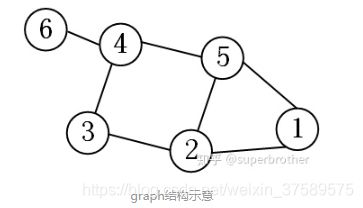
7.1 GCN 中的 Local Connectivity

1. 如果利用第一代 GCN，这个时候，可以发现这个卷积核没有 local 的性质，因为该卷积核得到的运算矩阵在所有位置上都有非 0 元素。换句话说，这是一个global 全连接的卷积核。
2. 如果是第二代 GCN 当 $K=0$ 卷积运算矩阵即为：$\left[\begin{array}{cccccc}{\alpha }_0& 0& 0& 0& 0& 0\\ 0& {\alpha }_0& 0& 0& 0& 0\\ 0& 0& {\alpha }_0& 0& 0& 0\\ 0& 0& 0& {\alpha }_0& 0& 0\\ 0& 0& 0& 0& {\alpha }_0& 0\\ 0& 0& 0& 0& 0& {\alpha }_0\end{array}\right]$。当 $K=1$ 卷积运算矩阵即为：$\left[\begin{array}{cccccc}{\alpha }_0+2{\alpha }_1& -{\alpha }_1& 0& 0& -{\alpha }_1& 0\\ -{\alpha }_1& {\alpha }_0+3{\alpha }_1& -{\alpha }_1& 0& -{\alpha }_1& 0\\ 0& -{\alpha }_1& {\alpha }_0+2{\alpha }_1& -{\alpha }_1& 0& 0\\ 0& 0& -{\alpha }_1& {\alpha }_0+3{\alpha }_1& -{\alpha }_1& -{\alpha }_1\\ -{\alpha }_1& -{\alpha }_1& 0& -{\alpha }_1& {\alpha }_0+3{\alpha }_1& 0\\ 0& 0& 0& -{\alpha }_1& 0& {\alpha }_0+{\alpha }_1\end{array}\right]$。当 $K=3$ 卷积运算矩阵即为：$\left[\begin{array}{cccccc}{\alpha }_0+2{\alpha }_1+6{\alpha }_2& -{\alpha }_1-4{\alpha }_2& {\alpha }_2& {\alpha }_2& -{\alpha }_1-4{\alpha }_2& 0\\ -{\alpha }_1-4{\alpha }_2& {\alpha }_0+3{\alpha }_1+12{\alpha }_2& -{\alpha }_1-5{\alpha }_2& 2{\alpha }_2& -{\alpha }_1-5{\alpha }_2& 0\\ {\alpha }_2& -{\alpha }_1-5{\alpha }_2& {\alpha }_0+2{\alpha }_1+6{\alpha }_2& -{\alpha }_1-5{\alpha }_2& 2{\alpha }_2& {\alpha }_2\\ {\alpha }_2& 2{\alpha }_2& -{\alpha }_1-5{\alpha }_2& {\alpha }_0+3{\alpha }_1+12{\alpha }_2& -{\alpha }_1-6{\alpha }_2& -{\alpha }_1-4{\alpha }_2\\ -{\alpha }_2-4{\alpha }_2& -{\alpha }_1-5{\alpha }_2& 2{\alpha }_2& -{\alpha }_1-6{\alpha }_2& {\alpha }_0+3{\alpha }_1+12{\alpha }_2& {\alpha }_2\\ 0& 0& {\alpha }_2& -{\alpha }_1-4{\alpha }_2& {\alpha }_2& {\alpha }_0+{\alpha }_1+2{\alpha }_2\end{array}\right]$。看一下图的邻接结构，卷积运算矩阵的非 0 元素都在 localize 的位置上。

7.2 GCN 中的 Parameter Sharing

7.2.1 第二代 GCN

$y=\sigma \left({\sum }_{j=0}^{K-1}{\alpha }_j{L}^{j}x\right)$，很明显 ${\alpha }_j$ 是可学习的参数，可以看到 ${\alpha }_j$ 与 $L^j$ 保持一致，我们知道 $L^j$ 对应着 $j$ 阶 neighbor，这意味着在同阶的邻居上参数共享（可以学习的参数相同），不同阶的邻居上参数不共享（可以学习的参数不同）。

优点：这样的共享方式是有“物理意义”的，因为我们知道 graph 通常本身是有 local stationary 性质的。也就是说随着 neighbor 阶数的增加，顶点间的相关性递减（相当于距离近的邻域内相关性强）。这种共享方式，本质上可以很容易实现上述性质。参数很少，如果是超大规模的图，可以利用这种方式。
缺点：参数太少了，只有 $K$ 个，使得模型无法很好地实现在同阶的邻域上分配不同的权重给不同的邻居（也就是 GAT 论文里说的 enable specifying different weights to different nodes in a neighborhood）

7.2.2 经典 GCN

$H^{l+1}=\sigma \left({\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{H}^l{W}^l\right)$
$H^0=x$

其中 $A$ 是 graph 的邻接短阵, $\hat{A}=A+I$ 是为了实现 self-accessible, $\hat{D}$ 是 $\hat{A}$ 中每个顶点的度矩阵。运算 ${\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}$ 是为了对 $\hat{A}$ 进行归一化, 防止在运算中出现数值不稳定的情况。

这个版本中, 记 $Y^l={\hat{D}}^{-\frac{1}{2}}\hat{A}{\hat{D}}^{-\frac{1}{2}}{H}^l$ ，这个运算可以理解为实现了空间信息的聚合，类似于下图。其中第 0 层的输入，是原始的特征，以后每增加一层，就会多聚合一阶 neighbor 上的信息（ $l$ 层就对每个顶点融合了 $l$ 阶邻域的信息) 。

很显然模型可学习的参数是 $W^l,Y^l{W}^l$ 进行了线性变换, 我个人认为是实现了 feature augment。也就是说模型在每一层共享了用于特征增强的参数变化矩阵。很显然, 这个矩阵维度与顶点数目或者每个顶点的度无关, 于是说这是一个在同层内顶点上共享的参数矩阵。

优点：这样的共享方式， W ${}^l$ 的维度是可以进行调节的，与顶点的数目无关，使得模型可以用于大规模的 graph 数据集。另一方面这个模型可以完成图结构 train 在 test 上不一样的任务。
缺点：这个模型对于同阶的邻域上分配给不同的邻居的权重是完全相同的（也就是 GAT 论文里说的无法 enable specifying different weights to different nodes in a neighborhood）。这一点限制了模型对于空间信息的相关性的捕捉能力，这也是在很多任务上不如 GAT 的根本原因。

8. 关于有向图问题

前面的理论推导都是关于无向图，如果是有向图问题，最大的区别就是邻接矩阵会变成非对称矩阵，这个时候不能直接定义拉普利矩阵及其谱分解（拉普拉斯矩阵本身是定义在无向图上的）。这个时候有两条思路解决问题：

• 要想保持理论上的完美，就需要重新定义图的邻接关系，保持对称性。
• 如果只是为了应用，有其他形式的 GCN 或者 GAT 可以处理有向图。

值得说明的是：GAT 作者写道“It is worth noting that, as Kipf & Welling (2017) and Atwood & Towsley (2016), our work can also be reformulated as a particular instance of MoNet (Monti et al., 2016). ” 也就是说本质上这些模型都可以认为是在重新定义了图的邻接关系后，再进行基本的卷积运算。

9. GCN的过度平滑问题

$y_{\text{output}}=\sigma \left({\sum }_{j=0}^{K-1}{\alpha }_j{L}^{j}x\right)$ 给出的卷积核中，含有拉普拉斯矩阵的 $j$ 次幂，当 $j$ 取值较大时，GCN学习到的特征可能会存在过度平滑现象，即每个顶点的输出特征都十分相似。这样就导致同一连通分量内的节点的表征会趋向于收敛到同一个值。从上一篇博客的热传导分析：GNN 实际是个热传导，所以如果导热率太高，时间太长，最终就是温度达到单一温度。所以要降低导热率，或者缩短传导时间，才能形成有局部特征的分布模式。