周志华《机器学习》第九章复习（带例题）

老师让我帮他出卷，就自己做了细纲出了点题。可以参考着复习。

考点：

1. 常用的性能度量指标，距离度量

2. 连续属性和离散属性的距离计算方法

3. 原型聚类（选择、填空、问答）

K均值聚类、学习向量量化、高斯混合聚类，这三种聚类方法的特点和方法思路

4. 密度聚类（选择、填空、判断、名词解释）

核心对象、密度直达、密度可达、密度相连，算法实现的核心思想

第九章 聚类（密度聚类没讲，层次聚类简要介绍）

1 无监督学习

       （填空）请写出使用无监督学习的其中两个原因：                    和                                   

答案：

1 原始数据容易获得，但标注数据昂贵

2 降低存储/计算

3 对高维数据降噪

3 对数据进行可视化操作

4 无监督学习通常可作为监督学习的预处理步骤。

2 聚类

       名词解释：对一批没有类别标签的样本集，按照样本之间的相似程度分类，相似的归为一类，不相似的归为其它类。

       判断： 矢量量化属于模型法聚类（×）

矢量量化属于网格法聚类（√）

3 性能度量（可出填空、简单大题）

名词解释：又称有效性指标，对于聚类结果，我们需通过某种性能度量来评估其好坏。如果明确了最终要使用的性能度量，则可直接将其作为聚类过程的优化目标，从而使聚类结果更好的符合要求。

判断：高斯混合模型属于利用内部指标进行性能度量的方法（×）

解释：高斯模型利用的是外部指标

       填空： 簇内相似度越高，簇间相似度越低，聚类质量越好。

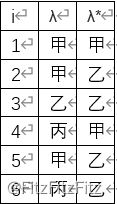
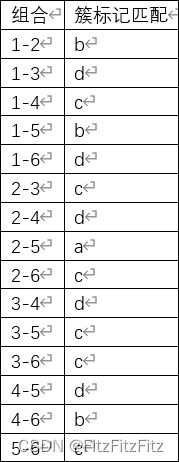
大题（考察性能度量基础应用，不涉及算法）：对数据集D= {x1,x2,. . . ,xm}，假定通过聚类得到的簇划分为C={C1,C2,. . . ,Ck}，参考模型给出的簇划分为C*= {C1*,C2*,…Cs* }，相应地，令λ与λ*分别表示与C和Ci*对应的簇标记向量。下表为对6个样本的聚类簇划分和参考模型簇划分，请列表回答每种λi和λj*的组合分别属于a=|SS|、b=|SD|、c=|DS|、d=|DD|的哪一种，并求出FMI指数。（提示：FMI指数为precision和recall值的几何平均）

（注：上课只有FMI稍微提了一下，也确实有可考性。）

 

答案

6*5/2=15，所以a+b+c+d=15

根据书上定义：

 

（15个组合一个一分）

所以有a=1，b=3，c=6，d=5；（本步骤不占分）

FMI==

（得到最终FMI得5分）

4 距离计算

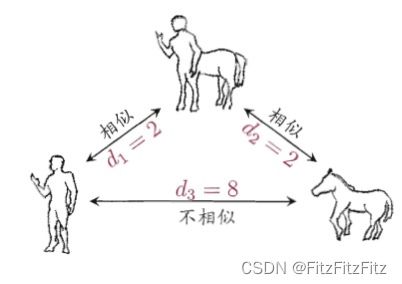
（填空）如图所示的距离度量方式不满足距离度量基本性质中的直递性。

（填空）|xi-xj|的Lp范数又被称为闵可夫斯基距离，当p=1时被称为曼哈顿距离（或街区距离），当p=2时被称为欧氏距离。

（判断）距离计算的预处理中，常用StandardScaler标准化，用Normalizer模一化，用MinMaxScaler区间缩放，处理之后的取值范围都在0和1之间。（×）

解释：StandardScaler标准化后的均值为0，方差为一，取值可能为负。

5  k-means

       （填空）k-means算法的优化目标是最小化平方误差，这是一个NP难问题，因此采用了贪心策略，通过迭代法（或坐标轴下降法）来近似求解；但这样不能保证收敛到全局最优，最普遍最简单的解决方案是运行多次取最好结果。

      

6 高斯混合模型（不好考名词解释，因为不好解释）

（填空）求解高斯混合模型使用了EM 算法:在每步迭代中,先根据当前参数来计算每个样本属于每个高斯成分的后验概率 (E步),再根据这个后验概率更新模型参数 (M步)，对高斯混合模型来说需要在M步更新的模型参数有均值向量，协方差矩阵，混合系数。

（判断）理论上来说，如果高斯混合模型融合的高斯模型个数足够多，它们之间的权重设定的足够合理，这个混合模型可以拟合任意分布的样本。（√）

8 层次聚类（讲了凝聚式聚类算法，没说他叫书上的AGNES）

(填空)请写出层次聚类的一个优点                     ，和一个缺点                   。

答案

优点：

1 不需要提前假定聚类的簇数

2 聚类结果对应着有意义的分类

缺点：

1 没有优化一个全局的目标函数

2 贪心：一旦簇被合并或拆分就不可逆