论文阅读笔记：Link Prediction Based on Graph Neural Networks

说明

Google学术PDF文稿连接
      本文为作者自己写的文章笔记。由于才刚刚大一结束，英文及学术水平有限，仅供参考。

Link Prediction Based on Graph Neural Networks

• Muhan Zhang
  Department of CSE
  Washington University in St. Louis
  [email protected]

• Yixin Chen
  Department of CSE
  Washington University in St. Louis
  [email protected]

Abstract

      本文介绍内容主要包含GNN进行链路预测问题的解答。传统Katz指标与共同邻居指标等方法具有较强的主观性，相当于模型建立时已经主观模拟了两个点可能连接的条件。基于这种传统方式的缺陷，引入一种学习机制，自主学习两个点连接可能性的计算方法。本文首先引入novel $\gamma$-decaying heuristic theory。然后引入GNN对链路进行预测。

1 Introduction

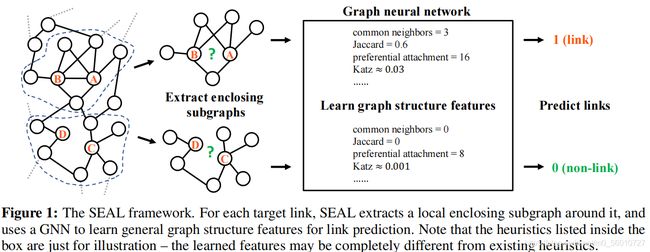
      传统的启发式方法具备过量的主观性(Although working well in practice, heuristic methods have strong assumptions on when links may exist.)，比如仅仅通过相同邻居数（CN方法）、Katz公式累计和（Katzs方法），并不一定真实显示实际情形的连接结构与链路引申概率。且此类方法仅仅利用了图像结构信息，即仅仅从无意义的临接矩阵中得到距离度量模式。
传统距离估算方法示例：

      一种提出的解决方法是Weisfeiler-Lehman Neural Machine (WLNM,“Weisfeiler-Lehman Neural Machine for Link Prediction”，谷歌学术PDF文章链接)，使用DNN简单的对这种连接模式进行预测。(Zhang and Chen[12] first studied this problem. They extract local enclosing subgraphs around links as the training data, and use a fully-connected neural network to learn which enclosing subgraphs correspond to link existence.)。这种方法首先对于每一条连边，提取K个以上邻居节点构成的子图。提取顺序是：先一阶邻居，再二阶邻居，以此类推；接着对提取的子图进行图编码，然后选择前K个进行提取。提取完子图之后为每个节点建立一个邻接矩阵（按照子图的哈希编码建立），将邻接矩阵输入到神经网络（文章使用的单隐藏层ANN分类器）中进行学习。
流程如下图所示：

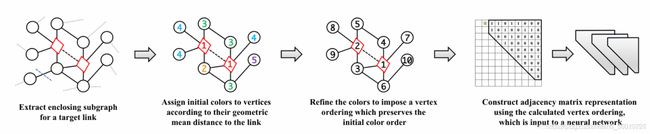
      然而上述方法存在着需要扩充h阶的情况，以求取前K哈希值的邻居节点。h是不确定的，并且很多情况下需要扩展到全图。本文提到了$\gamma$-theory可以证明经过预处理之后使用一个很小的h就可以达到相同的预测效果。
      通过改进，得到了一种新的方式SEAL(learning from Subgraphs, Embeddings and Attributes for
Link prediction)。首先使用GNN结合图像结构信息达到WLNM的效果，然后再综合节点本身带有的其他信息以达到预测的目的。其优势在于减少了计算的消耗并且不单单停留于节点的结构特征。

2 Preliminaries

Notations

      无向图(G=(V,E))，临接矩阵($A_{i,j}=1or0)$)，1-阶邻居($\Gamma (x)$)，点距($d(x,y)$)，路径($<x_0,x_1,\dots ,x_n>$)，路径长度($|<x_0,x_1,\dots ,x_n>|$)。

Latent features and explicit features

      隐式特征可以由deep walk(深度游走)等方法获得。显示特征则通常有attribute直接以点的特征形式给出。谷歌学术隐式特征获得方式Node2vec的PDF论文链接

Graph neural networks

      GNN形式在本文未详解，本文主要涉及应用。

Supervised heuristic learning

      关于与本文最相似的WLNM，其使用ANN，缺点一是必须把所有子图化作同一种形式，其二是临接矩阵形式仅仅只能学习图像结构信息，无法与隐式特征与显实特征结合，其三是缺乏理论支撑。

3 A theory for unifying link prediction heuristics

      提出了一种统一链路预测启发式算法的理论（后面几种情况主要是作统一理论论证，比较复杂）。主要是为后面的SEAL提供理论基础的。

Definition 1 (Enclosing subgraph)

      封闭子图$G_{i,j}^h$即所有距离点i,j任一小于等于h的所有点的集合。

Theorem 1

      任意h阶启发式可以由$G_{i,j}^h$得到。这里的启发式可以大致理解为相似性或连接概率的计算形式。本文接下来提出可以由一个较小的h得到较大H阶启发式。

Definition 2（$\gamma$-decaying heuristic）

$$H(x,y)=\eta \sum _{l=1}^{\infty }{\gamma }^{l}f(x,y,l)$$
      $\gamma$是一个0到1的衰弱因子，$\eta$是一个正常数或正值函数。f是一个正函数，x,y,l则分别为传入的两点与距离，即根据$G_{i,j}^h$求得，$l=ah+b$得到，这种设计可以使得不同阶对结果影响的差距几何级减小。

Theorem 2

      f(x,y,l)满足：$$1:f(x,y,z)⩽{\lambda }^l(\lambda <\frac{1}{\gamma })$$ $$2:H的误差随着h指数级减小$$
      这种构造形式有利于使用较小的h进行估计。

Lemma

      任何与x,y距离小于$2h+1$的路径都包含在$G_{i,j}^h$中。

3.1 Katz index

$$Kat{z}_{x,y}=\sum _{l=1}^{\infty }{\beta }^l|walk{s}^{<l>}|(x,y)|=\sum _{l=1}^{\infty }{\beta }^l[A^l](x,y)$$
      邻接矩阵A的l阶导可以简单的求得两个点之间长度为l的路径条数。Katz指数是上述的$\gamma$-decaying heuristic的一种特殊形式。

Proposition 1

$$[A^l{]}_{i,j}⩽d^l(d是最大的点的度数)$$

3.2 PageRank

      PageRank最初源自于网页推荐数值计算。PR值计算某一时刻，一个随机游走的访问者在网络图谱每一个点的存在概率。PR值的计算基于以下两个假设：
      数量假设：更重要的网页可能被更多的网页链接到。
      质量假设：有更高的 PageRank 的网页将会传递更高的权重。

Theorem 3

      PR值符合Theorem 2。

3.3 SimRank

      另一种启发式预测方法，实在懒得看了，以后用到再说。也是说明满足了性质。

Discussion

      除了上述三种形式，还有很多启发式方法都满足$\gamma$-衰弱启发的形式以及性质。对于后续的研究提供了仅仅使用局部子图可以几乎不损失图结构信息的理论支持。

4 SEAL: An implemetation of the theory using GNN

      SEAL是基于上述理论提出的链路预测模型，它包含三个步骤：

• 1）封闭子图提取
• 2）节点自主信息矩阵构造
• 3）GNN学习
• 从A comparative study of similarity-based and
  GNN-based link prediction approaches找到详细的叙述，本文没有提供一些重要细节。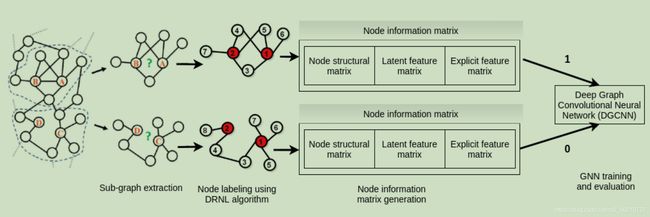

      首先将已知图像中所有可观察点标记为正边，所有未观测边记为负边（负边有一定标记出错概率），尽量去相同数量的正边与负边。使用GNN输入信息$(A,X)$，A为邻接矩阵，X为结构信息、节点嵌入信息与节点显式信息。

4.1 Node labeling

      节点标记使用整数函数$f_l(i)$进行表示。表示以某种方式进行排序后展示i在子图中的地位。标记方式需要满足的性质如下：1）需要研究的两个节点x,y标记为1。2）$f_l(i)=f_l(j)(dis(i,x)=dis(j,x)\bigcap dis(i,y)=dis(j,y))$。
      则使用标记方法Double-Radius Node Labeling (DRNL)：使用$(dis(i,x),dis(i,y))$元组进行测算，计算距离之和。可以得出一个哈希公式：$$f_l(i)=1+min(d_x,d_y)+(d/2)[(d/2)+(d\mathrm{m}\mathrm{o}\mathrm{d}2)-1]$$      其中$d=d(i,x)+d(i,y)$（注意对$d=+\infty$的情况标记为0）然后使用one-hot编码对节点位置标记进行储存。

4.2 Incorporating latent and explicit features

      得到每个点的embedding值，以及每个点的attribute基本信息。可以同时将三种信息输入GNN，通过标记的正边样本和负边样本进行链路预测学习。（本文基本没有讲细节）

5 Experimental results

      使用GNN，node2vec嵌入，在部分数据集得到了优异的效果（见原文）

6 Conclusions

      自动学习链接预测启发式是一个新领域。 在本文中，提出了一个γ-衰变统一了各种高阶启发式，并证明它们与局部学习的近似性。 受该理论的启发，提出了一种新颖的链接预测框架 SEAL，以同时从基于图的局部封闭子图、嵌入和属性中学习神经网络。 实验表明，SEAL 实现了较好的性能。 同时，作者希望 SEAL 不仅可以启发链接预测研究，还可以为其他领域开辟新的方向，例如知识图谱和推荐系统。