Pytorch实现DDPG算法

DDPG是强化学习里的一种经典算法。关于算法的原理我在之前的文章里有详细介绍过： 强化学习入门8—深入理解DDPG 。

在学习莫凡大神的教程中，莫凡大神用的是tensorflow实现的DDPG。因为平时使用pytorch较多，且大神当时使用的tensorflow版本也较低，于是便借此使用pytorch复现一下DDPG。

注意：本文参考的是莫凡大神的tf版本的代码，指路 https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/intro-DDPG/

回顾DDPG

DDPG即Deep Deterministic Policy Gradient，确定性策略梯度算法。它结构上基于Actor-Critic，结合DQN算法的思想，使得它不仅可以处理离散型动作问题，也可以处理连续型动作问题。

实现

话不多说，直接上代码

首先是定义Actor和Critic两个网络。

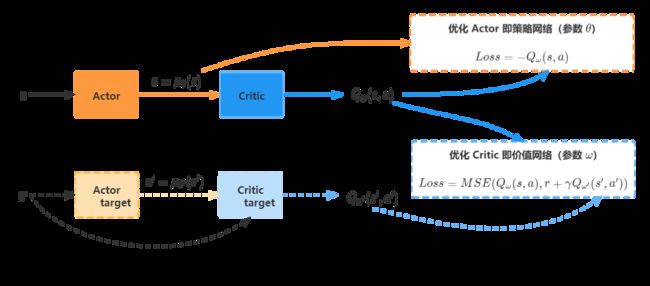
结合上面的图，Actor的输入是当前的state，然后输出的是一个确定性的action。

class Actor(nn.Module):
    def __init__(self, state_dim, action_dim, action_bound):
        super(Actor,self).__init__()
        self.action_bound = torch.FloatTensor(action_bound)
        # layer
        self.layer_1 = nn.Linear(state_dim, 30)
        nn.init.normal_(self.layer_1.weight, 0., 0.3) # 初始化权重
        nn.init.constant_(self.layer_1.bias, 0.1)
        
				self.output = nn.Linear(30, action_dim)
        self.output.weight.data.normal_(0.,0.3) # 初始化权重
        self.output.bias.data.fill_(0.1)

    def forward(self, s):
        a = torch.relu(self.layer_1(s))
        a = torch.tanh(self.output(a))
        # 对action进行放缩，实际上a in [-1,1]
        scaled_a = a * self.action_bound
        return scaled_a

在动作输出这里，加了一个 action bound 在，只是用于限制一下action的范围。

Critic网络输入的除了当前的state还有Actor输出的action，然后输出的是Q-value，即 Q(s,a)

class Critic(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(Critic,self).__init__()
        n_layer = 30
        # layer
        self.layer_1 = nn.Linear(state_dim, n_layer)
        nn.init.normal_(self.layer_1.weight, 0., 0.1)
        nn.init.constant_(self.layer_1.bias, 0.1)
        
        self.layer_2 = nn.Linear(action_dim, n_layer)
        nn.init.normal_(self.layer_2.weight, 0., 0.1)
        nn.init.constant_(self.layer_2.bias, 0.1)
        
        self.output = nn.Linear(n_layer, 1)

    def forward(self,s,a):
        s = self.layer_1(s)
        a = self.layer_2(a)
        q_val = self.output(torch.relu(s+a))
        return q_val

网络结构的定义比较简单。下面是DDPG如何学习这关键部分。

我们知道DDPG有一个记忆库，每次学习的数据是从记忆库中随机采样得来的。这部分实现比较简单。

需要注意的是，在学习过程中，两个网络的误差是不一样的。DDPG因为借鉴了DQN的思想，除了Actor和Critic两个网络外，还定义了各自的target网络。target网络的作用是计算下一时刻的Q值，方便TD-error的更新。TD-error的定义是

$$td\_error=MSE(Q(s,a),r+\gamma Q_{target}(s^{\prime },a^{\prime }))$$

Critic网络是根据 TD-error 来更新的。

# 训练critic
a_ = self.actor_target(bs_)
q_ = self.critic_target(bs_, a_)
q_target = br + self.gamma * q_
q_eval = self.critic(bs, ba)
td_error = self.mse_loss(q_target,q_eval)

而Actor网络是根据Q值来更新的，如下：

# 训练Actor
a = self.actor(bs)
q = self.critic(bs, a)
a_loss = -torch.mean(q)

这部分的完整代码如下：

class DDPG(object):
    def __init__(self, state_dim, action_dim, action_bound, replacement,memory_capacticy=1000,gamma=0.9,lr_a=0.001, lr_c=0.002,batch_size=32) :
        super(DDPG,self).__init__()
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.memory_capacticy = memory_capacticy
        self.replacement = replacement
        self.t_replace_counter = 0
        self.gamma = gamma
        self.lr_a = lr_a
        self.lr_c = lr_c
        self.batch_size = batch_size
        # 记忆库
        self.memory = np.zeros((memory_capacticy, state_dim * 2 + action_dim + 1))
        self.pointer = 0
        # 初始化 Actor 网络
        self.actor = Actor(state_dim, action_dim, action_bound)
        self.actor_target = Actor(state_dim, action_dim, action_bound)
        # 初始化 Critic 网络
        self.critic = Critic(state_dim,action_dim)
        self.critic_target = Critic(state_dim,action_dim)
        # 定义优化器
        self.aopt = torch.optim.Adam(self.actor.parameters(), lr=lr_a)
        self.copt = torch.optim.Adam(self.critic.parameters(), lr=lr_c)
        # 选取损失函数
        self.mse_loss = nn.MSELoss()
    
		# 从记忆库中随机采样    
    def sample(self):
        indices = np.random.choice(self.memory_capacticy, size=self.batch_size)
        return self.memory[indices, :] 

    def choose_action(self, s):
        s = torch.FloatTensor(s)
        action = self.actor(s)
        return action.detach().numpy()

    def learn(self):

        # soft replacement and hard replacement
        # 用于更新target网络的参数
        if self.replacement['name'] == 'soft':
            # soft的意思是每次learn的时候更新部分参数
            tau = self.replacement['tau']
            a_layers = self.actor_target.named_children()
            c_layers = self.critic_target.named_children()
            for al in a_layers:
                a = self.actor.state_dict()[al[0]+'.weight']
                al[1].weight.data.mul_((1-tau))
                al[1].weight.data.add_(tau * self.actor.state_dict()[al[0]+'.weight'])
                al[1].bias.data.mul_((1-tau))
                al[1].bias.data.add_(tau * self.actor.state_dict()[al[0]+'.bias'])
            for cl in c_layers:
                cl[1].weight.data.mul_((1-tau))
                cl[1].weight.data.add_(tau * self.critic.state_dict()[cl[0]+'.weight'])
                cl[1].bias.data.mul_((1-tau))
                cl[1].bias.data.add_(tau * self.critic.state_dict()[cl[0]+'.bias'])
            
        else:
            # hard的意思是每隔一定的步数才更新全部参数
            if self.t_replace_counter % self.replacement['rep_iter'] == 0:
                self.t_replace_counter = 0
                a_layers = self.actor_target.named_children()
                c_layers = self.critic_target.named_children()
                for al in a_layers:
                    al[1].weight.data = self.actor.state_dict()[al[0]+'.weight']
                    al[1].bias.data = self.actor.state_dict()[al[0]+'.bias']
                for cl in c_layers:
                    cl[1].weight.data = self.critic.state_dict()[cl[0]+'.weight']
                    cl[1].bias.data = self.critic.state_dict()[cl[0]+'.bias']
            
            self.t_replace_counter += 1

        # 从记忆库中采样bacth data
        bm = self.sample()
        bs = torch.FloatTensor(bm[:, :self.state_dim])
        ba = torch.FloatTensor(bm[:, self.state_dim:self.state_dim + self.action_dim])
        br = torch.FloatTensor(bm[:, -self.state_dim - 1: -self.state_dim])
        bs_ = torch.FloatTensor(bm[:,-self.state_dim:])
        
        # 训练Actor
        a = self.actor(bs)
        q = self.critic(bs, a)
        a_loss = -torch.mean(q)
        self.aopt.zero_grad()
        a_loss.backward(retain_graph=True)
        self.aopt.step()
        
        # 训练critic
        a_ = self.actor_target(bs_)
        q_ = self.critic_target(bs_, a_)
        q_target = br + self.gamma * q_
        q_eval = self.critic(bs, ba)
        td_error = self.mse_loss(q_target,q_eval)
        self.copt.zero_grad()
        td_error.backward()
        self.copt.step()

    # 存储序列数据
    def store_transition(self, s, a, r, s_):
        transition = np.hstack((s,a,[r],s_))
        index = self.pointer % self.memory_capacticy
        self.memory[index, :] = transition
        self.pointer += 1

一些trick

soft-replacement

在实现过程中，我们的target网络也是要更新参数，实际上target参数的更新是来源于估计网络（也就是原Actor、Critic网络）。对于参数更新有两种方法：

• hard replacement 每隔一定的步数才更新全部参数，也就是将估计网络的参数全部替换至目标网络
• soft replacement 每一步就更新，但是只更新一部分参数。

add noise to action

在action的选择策略上增加explore。

实际上就是通过增加一些随机噪声，来增加一些动作空间的探索。实现上就是调整方差。

---

最后，完整代码已放置于github。