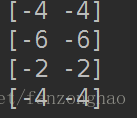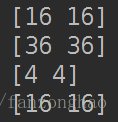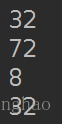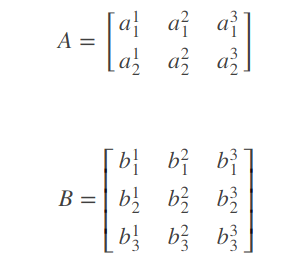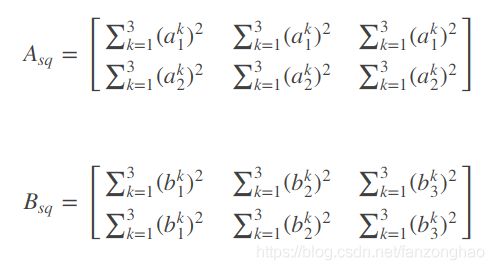实现两个点集的欧式距离和cos距离和索引值寻找(含有两种解法,for循环和矩阵操作)
一.计算欧式距离
1,直接for循环
两个点集points1,points2,用dist来存储距离
points1=np.array([[1,2],[3,4]])
points2 = np.array([[5, 6],[7,8]])
dist = np.zeros(shape=[points1.shape[0],points2.shape[0]])
for i in range(points1.shape[0]):
for j in range(points2.shape[0]):
print(points1[i, :] - points2[j, :])遍历两个点集的索引相减值
加上这句话
print(np.square(points1[i, :] - points2[j, :]))print(np.sum(np.square(points1[i, :] - points2[j, :])))print(np.sqrt(np.sum(np.square(points1[i, :] - points2[j, :]))))points1=np.array([[1,2],[3,4]])
points2 = np.array([[5, 6],[7,8]])
dist = np.zeros(shape=[points1.shape[0],points2.shape[0]])
for i in range(points1.shape[0]):
for j in range(points2.shape[0]):
# print(points1[i, :] - points2[j, :])
# print('======================')
# print(np.square(points1[i, :] - points2[j, :]))
# print('============================')
# print(np.sum(np.square(points1[i, :] - points2[j, :])))
# print(np.sqrt(np.sum(np.square(points1[i, :] - points2[j, :]))))
dist[i, j] = np.sqrt(np.sum(np.square(points1[i, :] - points2[j, :])))
print(dist)ind = np.unravel_index(np.argmax(dist), dist.shape)
print(ind)返回索引值
2,矩阵操作求欧式距离
假设有两个三维向量集,用矩阵表示:
要求A,B这两个矩阵中的元素两两之间的欧式距离。
先求出:
然后对![]() 和
和![]() 分别求其中每个向量的模平方,并扩展为2*3矩阵:
分别求其中每个向量的模平方,并扩展为2*3矩阵:
然后:
将上面这个矩阵一开方,就得到了A,B矩阵各个元素两两之间的欧式距离。
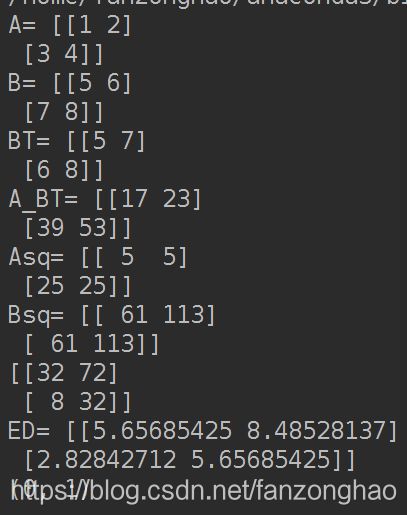
import numpy as np
A=np.array([[1,2],
[3,4]])
print('A=',A)
B=np.array([[5,6],
[7,8]])
print('B=',B)
BT=np.transpose(B)
print('BT=',BT)
A_BT=np.dot(A,BT)
print('A_BT=',A_BT)
Asq=A**2
Asq=np.tile(np.sum(Asq,axis=1,keepdims=True),(1,A_BT.shape[1]))
print('Asq=',Asq)
Bsq=BT**2
Bsq=np.tile(np.sum(Bsq,axis=0,keepdims=True),(A_BT.shape[0],1))
print('Bsq=',Bsq)
print(Asq+Bsq-2*A_BT)
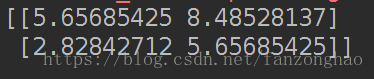
ED=np.sqrt(Asq+Bsq-2*A_BT)
print('ED=',ED)
ind=np.unravel_index(np.argmax(ED),ED.shape)
print(ind)
print(ED[ind[0],ind[1])二.计算cos距离
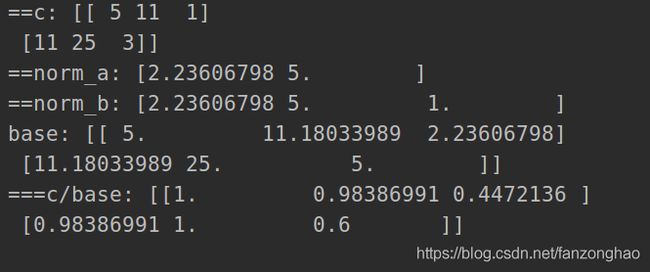
import numpy as np
a = np.array([[1, 2],
[3, 4]])
b = np.array([[1, 2],
[3, 4],
[1, 0]])
c = np.dot(a, np.transpose(b))
print('==c:', c)
norm_a = np.sqrt(np.sum(np.square(a), axis=-1))
print('==norm_a:', norm_a)
norm_b = np.sqrt(np.sum(np.square(b), axis=-1))
print('==norm_b:', norm_b)
base = np.dot(norm_a.reshape(norm_a.shape[0], 1), norm_b.reshape(1, norm_b.shape[0]))
print('base:', base)
print('===c/base:', c/base)