限制性立方样条(Restricted Cubic Spline)
限制性立方样条(Restricted Cubic Spline)
- 一、背景
-
- (一)什么是线性 (Linearity) ?
- (二)为什么要做线性假设?
- (三)如何面对非线性的难题?
- (四)多项式回归
- 二、样条函数
-
- (一)样条 (Spline) 的定义
-
- 1. 原始定义
- 2. 数学定义
- (二)节点的选择
-
- 1. 节点 (knots)
- 2. R软件拟合示例
- (三)样条的分类
-
- 1. B-splines(B样条/多次回归样条)
- 2. Natural splines(自然样条/限制性立方样条)
- 三、限制性立方样条
-
- (一)定义
- (二)RCS节点的数量和位置
- (三)R软件rms程序包操作示例
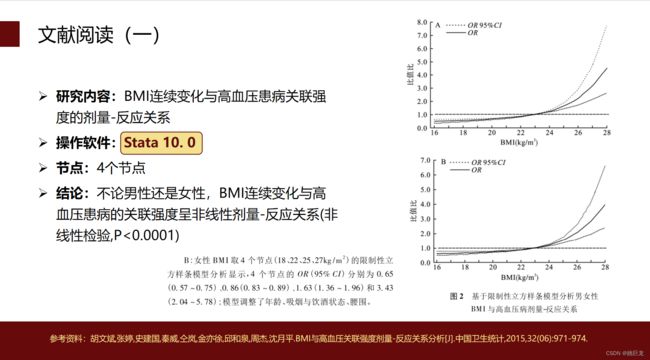
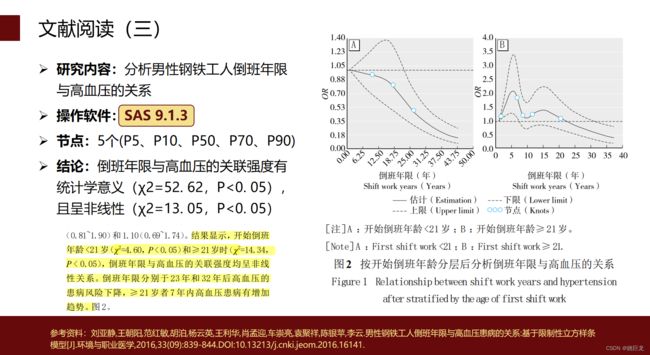
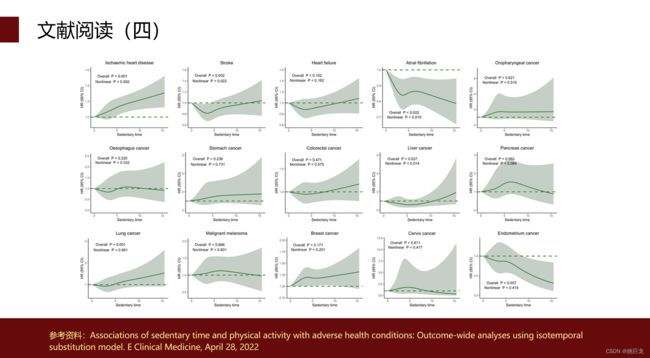
- 四、相关文献阅读
- 参考文献
在上一篇文章等时替代模型的案例论文中,我们可以看到,COX比例风险回归模型中的连续变量可能会对生存时间产生非线性风险,如果不考虑这个风险,就会对结果造成偏差。非线性关系的拟合思路是在线性关系上加入高次项,如二次项和三次项,这样就构成了高次多项式模型。因此,作者对于非线性趋势的拟合采用了限制性立方样条(restricted cubic spline,RCS)的方法,其中也简单提到了,RCS是用来拟合自变量和因变量之间非线性关系的一个好方法。
限制性立方样条函数属于多项式中的一种,最大的特点在于它进行了样条插值并对趋势首尾两端进行了线性限制,即在第一个节点前的趋势和最后一个节点后的趋势强制限制为线性。在这篇文章中,笔者就将对限制性立方样条的原理和案例进行总结。
一、背景
(一)什么是线性 (Linearity) ?
维基百科的定义:
Linearity is the property of a mathematical relationship (function) that can be graphically represented as a straight line. 1
线性是指可以用图形表示为直线的数学关系或函数
Additivity: f(x + y) = f(x) + f(y).
Homogeneity of degree 1: f(αx) = α f(x) for all α.
对于多维函数的推广,线性是指函数兼容加法和定标的性质,也称为叠加原理
(二)为什么要做线性假设?
线性是建立线性回归模型时的常见假设。
因为现实世界里面许多量之间具有线性或者近似线性的依赖关系,即使不是线性关系,我们对变量进行适当的变换,得到的新的变量可能也会具有近似的线性关系。一旦问题落脚到线性问题,那在数学里面积累的大量的、丰富的处理线性关系的理论和方法就能用上了。
而且线性模型具有一个最大的优势,就是易于解释。在线性关系中,连续变量在整个变量范围内具有相同的影响。
例如,在传统的等时替代模型中,我们用系数b代表替代效应。系数b1就表示在保持总体活动时间不变的情况下,用其他活动去替换x1的时候,对健康结果变量y的估计效果。
这很容易理解,线性使得估计易于解释,也让传统的模型更具有优势:模型中每增加一个单位就会给出相应系数在结果中的变化。
但是,要知道,自然界中的规律很难会遵循一条简单的直线。对于今天的这些复杂的大型数据集,我们的模型应该允许,也必须允许非线性效应的存在。
(三)如何面对非线性的难题?
有许多非线性替代方案可以帮助我们去面对这些非线性的难题,从而更好地找到变量之间的联系。
这些替代方案大多数都依赖于将单个连续变量转换为多个。其中最简单的方法就是把变量转换为多项式。
例如,下面这个模型:
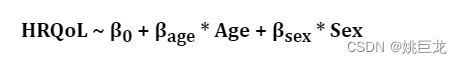
我们可以对年龄这个变量进行扩展,让它还包括年龄的平方:
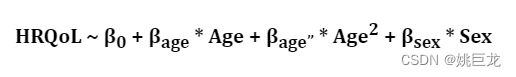
变成多项式后,所得的就是曲线了。这样就产生了一个问题,当我们添加平方项后,前面的系数就变得难以解释,并且如果我们再添加三次项,即Age³,那前面的系数就几乎不可能解释了。
正是由于这种解释困难,我们要么使用 rms::contrast 函数,要么使用stats::predict来说明变量的行为方式。
(四)多项式回归
本篇文章的案例数据均来自下面随机生成的数据:
options(max.print=25)
set.seed(76)
f <- function(x){
f_x <- 0.2*x^11*(10*(1-x))^6+10*(10*x)^3*(1-x)^10
return(f_x)
}
values <- data_frame(
x = seq(from=0, to=1, length=500),
f_x = f(x),
eps = rnorm(n=500, mean=0, sd=2),
y = f_x + eps
)
values %>%
ggplot(aes(x=x)) +
stat_function(fun = f) +
geom_point(aes(y=y))
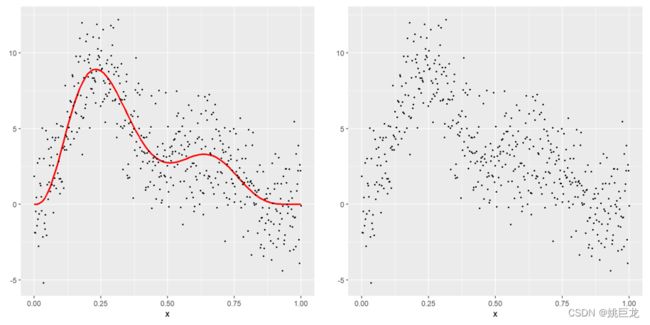
对于函数f,在范围(0,1)上按照期望为0,方差为2的正态分布,随机产生500个噪点,结果如下图:
对噪点分别进行一次、二次、三次、四次多项式回归:
ggplot(values,aes(x=x,y=y))+geom_point()
lmp1=lm(y~poly(x,1),data = values)
poly1=predict(lmp1,values)
values$poly1=poly1
lmp2=lm(y~poly(x,2),data = values)
poly2=predict(lmp2,values)
values$poly2=poly2
lmp3=lm(y~poly(x,3),data = values)
poly3=predict(lmp3,values)
values$poly3=poly3
lmp4=lm(y~poly(x,4),data = values)
poly4=predict(lmp4,values)
values$poly4=poly4
valueslong=gather(values,key="model",value = "value",
c("poly1","poly2","poly3","poly4"))
ggplot(valueslong)+theme_bw()+geom_point(aes(x,y))+
geom_line(aes(x=x,y=value,linetype=model,colour=model),size=1.0)+
theme_update(axis.title.y=element_blank())
多项式的使用是一种粗略的估算方法,具有可以产生平滑拟合的优点,但是它所拟合的函数也十分复杂,最大的缺点就是不灵活。
例如,二次曲线的形状必须是“U”形(或倒“U”形)——上升的必须以相同的速度下降;多项式通常会导致曲线在末端不能很好地拟合数据。
因此,对于多项式,我们也需要找到更好的方法去替代它,本篇文章所要介绍的方法——样条曲线 (Spline) ,就是一类灵活的替代函数。
二、样条函数
(一)样条 (Spline) 的定义
1. 原始定义
样条(spline)原本是指工匠的工具,它是一种灵活的细木条或金属条,用来绘制平滑曲线。一般会用几个重物施加在工具的不同位置,让条带根据重物的数量和位置发生弯曲。
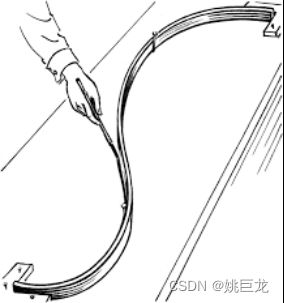
2. 数学定义
类似的作用,样条曲线用于统计,是为了方便在数学上重现灵活的形状。样条曲线本质是一个分段多项式函数,此函数受限于某些控制点,称为 “节点”,节点放置在数据范围内的多个位置,多项式的类型以及节点的数量和位置决定了样条曲线的类型。
样条函数是一组平滑连接的分段多项式。 “平滑连接”意味着对于 n 次多项式,样条函数及其前 n-1 阶导数在节点处都是连续的。
(二)节点的选择
1. 节点 (knots)
如果使用 k 个结,拟合 n 次多项式需要 k + n + 1 个回归参数(包括截距)。
在实践中,通常使用三次样条(即 3 次多项式),除截距外还需要 k + 3 个系数,而拟合线性模型只需 1 个系数。 这是允许拐点的多项式的最小度数,为拟合数据提供了足够的灵活性,同时不像高阶样条那样需要那么多的自由度。 由于一阶和二阶导数(斜率和斜率的变化率)在节点处是连续的,三次样条曲线在外观上是平滑的2。

2. R软件拟合示例
R示例:
library(tidyverse)
library(broom)
df_values <- c(2, 5, 10, 15, 25, 50)
overall <- NULL
for(df in df_values){
overall <- smooth.spline(values$x, values$y, df=df) %>%
augment() %>%
mutate(df=df) %>%
bind_rows(overall)
}
multiple_df <- overall %>%
ggplot(aes(x=x)) +
geom_point(aes(y=y)) +
geom_line(aes(y=.fitted)) +
facet_wrap(~df, nrow=2) +
labs(title="Splines fit with different degrees of freedom")
multiple_df +
stat_function(fun = f)
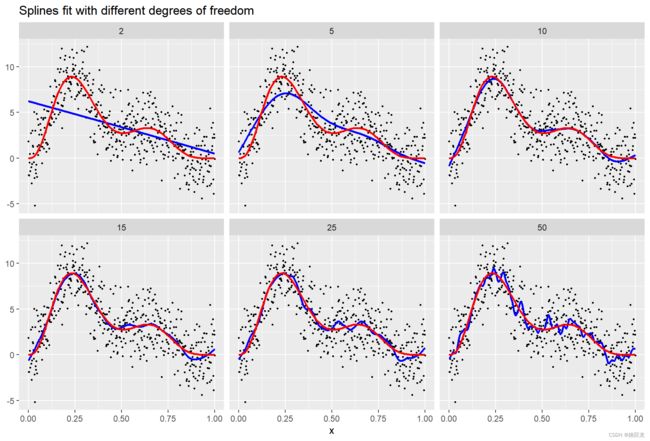
如下图所示,是节点分别为2、5、10、15、25、50时,利用R软件,对黑色噪点进行拟合得到的图形。(蓝色是拟合曲线,红色是真实曲线)
(三)样条的分类
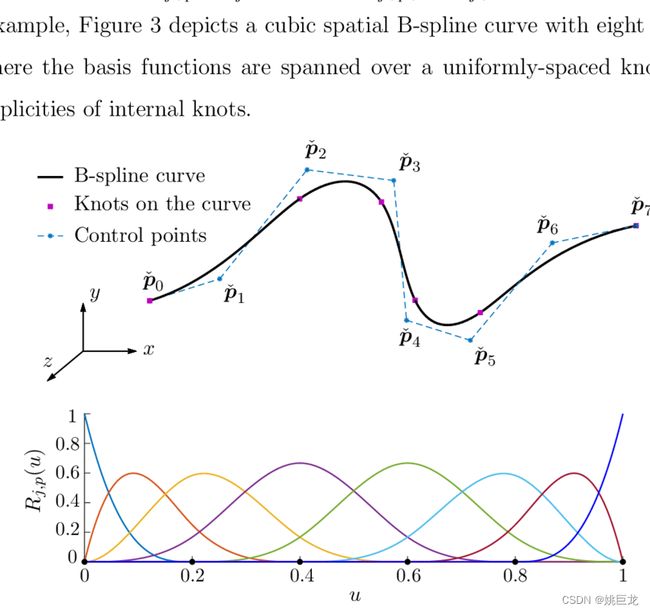
1. B-splines(B样条/多次回归样条)
如果样条是基曲线的线性组合, 则称为B样条(B-spline)
基函数为:
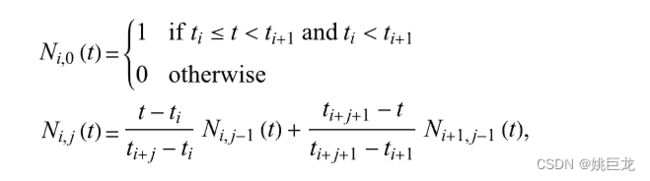
B-spline定义为:
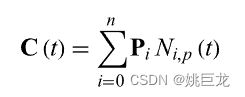
2. Natural splines(自然样条/限制性立方样条)
‘Natural Cubic Spline’ — is a piece-wise cubic polynomial that is twice continuously differentiable. It is considerably ‘stiffer’ than a polynomial in the sense that it has less tendency to oscillate between data points.

三、限制性立方样条
(一)定义
回归样条(regression spline)本质上是一个分段多项式,但它一般要求每个分段点上连续并且二阶可导。
即:设自变量数据的范围在区间[a,b],并根据需要分成k个段:a = t0 < t1 < … < tk-1 < tk = b,在每个区间 [ti-1,ti) 分别用一个多项 Si(x) 式表示,则回归样条 f(x) = Si(x) 当 x∈[ ti-1,ti ),并且 f ″(x) 在 [a,b] 存在连续3。
限制性立方样条 (restricted cubic spline,RCS) 是在回归样条的基础上附加要求:样条函数在自变量数据范围两端的两个区间 [t0,t1) 和 (tk-1,tk] 内是线性函数,满足上述性质的样条函数通常用 RCS(X) 表示,其表达式为:
(二)RCS节点的数量和位置
结的数量比位置更重要。有研究表明,五个结足以很好地适应实践中可能出现的任何模式。
Harrell (2010) 指出“对于许多数据集,k = 4 提供了模型的充分拟合,并且是在灵活性和由过度拟合小样本引起的位置损失之间的良好折衷”4。
- 如果样本量很小,则应使用三个节点,以便在节点之间有足够的观测值,以便能够拟合每个多项式。
- 如果样本量很大并且有理由相信所研究的关系变化很快,则可以使用超过 5 个节点。
对于一些研究,理论可能会暗示结的位置。更常见的是,节点的位置是根据连续变量的分位数预先指定的,这确保了每个区间中有足够的观测值来估计三次多项式。

(三)R软件rms程序包操作示例
x = seq(from=0, to=1, length=500)
y = f(x)
model <- lm(y ~ x)
# restricted cubic spline
model.spline1 <- lm(y ~ rcs(x, 3))
model.spline2 <- lm(y ~ rcs(x, 5))
model.spline3 <- lm(y ~ rcs(x, 7))
model.spline4 <- lm(y ~ rcs(x, 9))
model.spline5 <- lm(y ~ rcs(x, 10))
# compare models (to determine number of knots)
AIC(model.spline1,model.spline2,model.spline3,model.spline4,model.spline5)
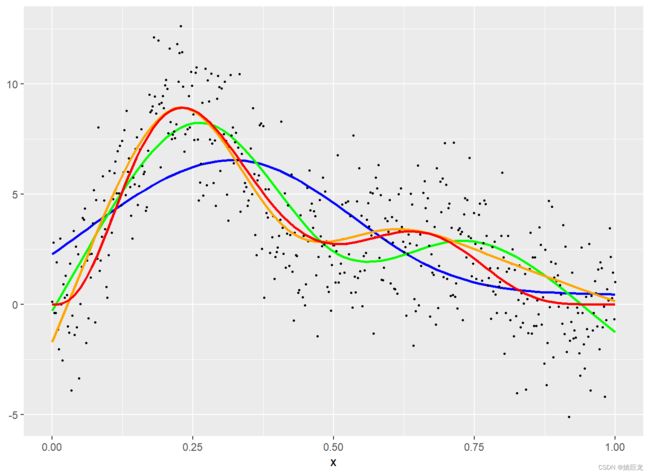
ggplot(data=values, aes(x=x, y=y)) +
geom_point()+geom_smooth(aes(x=x, y=y),
method="lm", formula=y ~ rcs(x, 3),
se=FALSE, colour="blue") +
geom_point()+geom_smooth(aes(x=x, y=y),
method="lm", formula=y ~ rcs(x, 5),
se=FALSE, colour="red") +
geom_point()+geom_smooth(aes(x=x, y=y),
method="lm", formula=y ~ rcs(x, 9),
se=FALSE, colour="orange")
四、相关文献阅读
参考文献
维基百科:https://en.wikipedia.org/wiki/Linearity ↩︎
Croxford, Ruth. “Restricted Cubic Spline Regression : A Brief Introduction.” (2016). ↩︎
罗剑锋,金欢,李宝月,赵耐青.限制性立方样条在非线性回归中的应用研究[J].中国卫生统计,2010,27(03):229-232. ↩︎
Harrell, F.E. (2010) Regression Modeling Strategies: with applications to linear models, logistic regression, and survival analysis. Springer-Verlag New York, Inc. New York, USA. ↩︎