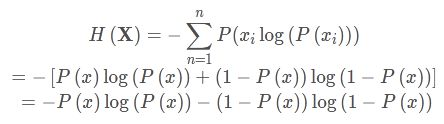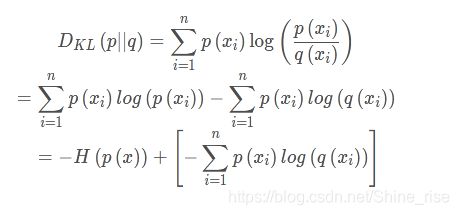机器学习笔记week2——最大似然估计,交叉熵,分类指标F1、ROC等
文章目录
-
- 1 梯度更新方式
-
-
- 1.1 凸集
- 1.2 凸函数
-
- 2 线性回归矩阵形式
-
-
- 2.1 奇异矩阵
-
- 3 最大似然估计
- 4 逻辑回归
-
-
- 4.1 交叉熵损失函数
-
- 5 分类指标
1 梯度更新方式
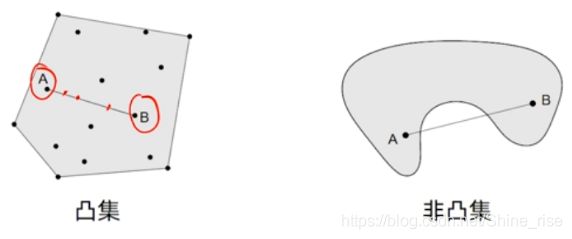
1.1 凸集
凸集:一个点集 S 被称为凸集,当且仅当该 S 里的任意两点 A 和 B 的连线上任意一点同样属于 S
t x 1 + ( 1 − t ) x 2 ∈ S t x_{1}+(1-t) x_{2} \in S tx1+(1−t)x2∈S
for all x 1 , x 2 ∈ S , 0 ≤ t ≤ 1 x_{1}, x_{2} \in S, 0 \leq t \leq 1 x1,x2∈S,0≤t≤1
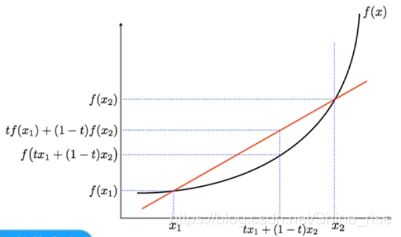
1.2 凸函数
凸函数: f : R n → R f: \mathbb{R}^{n} \rightarrow \mathbb{R} f:Rn→R是凸函数: dom f 是一个凸集,并且满足
f ( t x 1 + ( 1 − t ) x 2 ) ≤ t f ( x 1 ) + ( 1 − t ) f ( x 2 ) f\left(t x_{1}+(1-t) x_{2}\right) \leq t f\left(x_{1}\right)+(1-t) f\left(x_{2}\right) f(tx1+(1−t)x2)≤tf(x1)+(1−t)f(x2)
∀ x 1 , x 2 ∈ dom f , 0 ≤ t ≤ 1 \forall x_{1}, x_{2} \in \operatorname{dom} f, 0 \leq t \leq 1 ∀x1,x2∈domf,0≤t≤1
注意:凸函数不一定都可导,比如 relu 函数是凸函数,不可导
2 线性回归矩阵形式
2.1 奇异矩阵
- 奇异矩阵:行列式为 0 的矩阵,不可逆矩阵
- 非奇异矩阵:行列式不为 0 的矩阵,可逆矩阵
3 最大似然估计
一般来说,我们解决分类问题有三种思路:(1)判别函数方法;(2)判别式方法;(3)生成式方法
判别函数方法是指,找到一个判别函数f(x),该函数能够把每个输入 x 直接映射为类别标签。例如,在二分类问题中,f(·)可能是一个二元的数值,f = 0表示类别C1,f = 1表示类别C2。当我们输入一个x的时候,函数直接输出的是类别,在这种情况下,概率不起作用;
判别式方法是指,首先解决确定后验类密度p(Ck | x)这一推断问题,接下来使用决策论来对新的输入x进行分类。
生成式方法是指,首先对于每个类别Ck,独立地确定类条件密度p(x |Ck)。这是一个推断问题。然后,推断先验类概率p(Ck)。之后,使用贝叶斯定理求出后验类概率p(Ck | x)。得到后验概 率之后,我们可以使用决策论来确定每个新的输入x的类别。
- 方法1的优势在于及其简单,但是它缺少了对于后验概率的计算,而我们在很多时候其实都是需要后验概率的存在的(比如对最小化风险、拒绝选项、补偿类先验概率、组合模型的研究场景);
- 方法2的优势在于比较节约计算资源,但是其缺陷在于对于低概率的新数据点来说有点难以预测 ;
- 方法3的优势在于可以求解得到边缘概率密度,有利于离群点检测
4 逻辑回归
4.1 交叉熵损失函数
转自链接https://blog.csdn.net/b1055077005/article/details/100152102
信息量:
信息奠基人香农(Shannon)认为“信息是用来消除随机不确定性的东西”,也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。
“太阳从东边升起”,这条信息并没有减少不确定性,因为太阳肯定是从东边升起的,这是一句废话,信息量为0。
”2018年中国队成功进入世界杯“,从直觉上来看,这句话具有很大的信息量。因为中国队进入世界杯的不确定性因素很大,而这句话消除了进入世界杯的不确定性,所以按照定义,这句话的信息量很大。
根据上述可总结如下:信息量的大小与信息发生的概率成反比。概率越大,信息量越小。概率越小,信息量越大。
设某一事件发生的概率为P(x),其信息量表示为: I ( x ) = − log ( P ( x ) ) I(x)=-\log (P(x)) I(x)=−log(P(x))
其中I(x)表示信息量,这里log表示以e为底的自然对数。
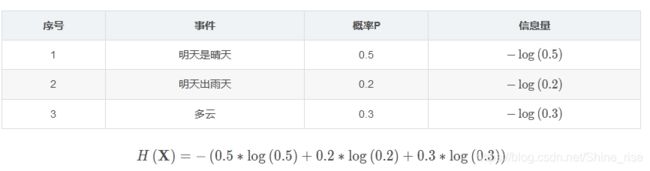
信息熵:
信息熵也被称为熵,用来表示所有信息量的期望。
期望是试验中每次可能结果的概率乘以其结果的总和。
所以信息量的熵可表示为:(这里的X是一个离散型随机变量)
H ( X ) = − ∑ i = 1 n P ( x i ) log ( P ( x i ) ) ) ( X = x 1 , x 2 , x 3 … , x n ) \left.H(\mathbf{X})=-\sum_{i=1}^{n} P\left(x_{i}\right) \log \left(P\left(x_{i}\right)\right)\right) \quad\left(\mathbf{X}=x_{1}, x_{2}, x_{3} \ldots, x_{n}\right) H(X)=−∑i=1nP(xi)log(P(xi)))(X=x1,x2,x3…,xn)
对于0-1分布的问题,由于其结果只用两种情况,是或不是,设某一件事情发生的概率为P(x),则另一件事情发生的概率为1−P(x),所以对于0-1分布的问题,计算熵的公式可以简化如下:
相对熵(KL散度):
如果对于同一个随机变量X有两个单独的概率分布P(x)和Q(x),则我们可以使用KL散度来衡量这两个概率分布之间的差异。
下面直接列出公式,再举例子加以说明。
D K L ( p ∥ q ) = ∑ i = 1 n p ( x i ) log ( p ( x i ) q ( x i ) ) D_{K L}(p \| q)=\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(\frac{p\left(x_{i}\right)}{q\left(x_{i}\right)}\right) DKL(p∥q)=∑i=1np(xi)log(q(xi)p(xi))
在机器学习中,常常使用P(x)来表示样本的真实分布,Q(x)来表示模型所预测的分布,比如在一个三分类任务中(例如,猫狗马分类器),x1,x2,x3分别代表猫,狗,马,例如一张猫的图片真实分布P(X)=[1,0,0], 预测分布Q(X)=[0.7,0.2,0.1],计算KL散度:
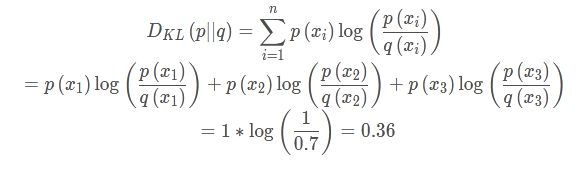
KL散度越小,表示P(x)与Q(x)的分布更加接近,可以通过反复训练Q(x)来使Q(x)的分布逼近P(x)
交叉熵:
前者H(p(x))表示信息熵,后者即为交叉熵,KL散度 = 交叉熵 - 信息熵
交叉熵公式表示为:
H ( X ) = − ∑ i = 1 n P ( x i ) log ( Q ( x i ) ) ) ( X = x 1 , x 2 , x 3 … , x n ) \left.H(\mathbf{X})=-\sum_{i=1}^{n} P\left(x_{i}\right) \log \left(Q\left(x_{i}\right)\right)\right) \quad\left(\mathbf{X}=x_{1}, x_{2}, x_{3} \ldots, x_{n}\right) H(X)=−∑i=1nP(xi)log(Q(xi)))(X=x1,x2,x3…,xn)
在机器学习训练网络时,输入数据与标签常常已经确定,那么真实概率分布P(x)也就确定下来了,所以信息熵在这里就是一个常量。由于KL散度的值表示真实概率分布P(x)与预测概率分布Q(x)之间的差异,值越小表示预测的结果越好,所以需要最小化KL散度,而交叉熵等于KL散度加上一个常量(信息熵),且公式相比KL散度更加容易计算,所以在机器学习中常常使用交叉熵损失函数来计算loss就行了。
交叉熵在单分类问题中的应用:
在线性回归问题中,常常使用MSE(Mean Squared Error)作为loss函数,而在分类问题中常常使用交叉熵作为loss函数。
下面通过一个例子来说明如何计算交叉熵损失值。
假设我们输入一张狗的图片,标签与预测值如下:
总结:
- 交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
- 交叉熵在分类问题中常常与softmax是标配,softmax将输出的结果进行处理,使其多个分类的预测值和为1,再通过交叉熵来计算损失。
5 分类指标
-
accuracy:所有样本中预测准确的概率
-
precision:所有预测准确的样本中,真实值为1的概率
-
recall:所有真实值为1的样本中,预测准确的概率
-
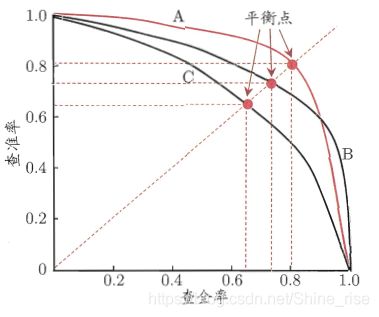
P-R曲线:Precision-Recall曲线
P-R曲线如下:(受正负样本的比例影响较大)
-
False Positive Rate:所有真实值为0的样本中,预测值为1的概率
-
True Positive Rate:所有真实值为1的样本中,预测值为1的概率
-
F1 score:Precision 和 recall 的调和平均数
F 1 = 2 1 Precision + 1 R e c a l l = 2 × Precision × R e c a l l Precision + R e c a l l \mathrm{F} 1=\frac{2}{{\frac{1}{\text { Precision}}}+{\frac{1}{\mathrm{Recall}}}}=\frac{2 \times \text { Precision } \times \mathrm{Recall}}{\text { Precision }+\mathrm{Recall}} F1= Precision1+Recall12= Precision +Recall2× Precision ×Recall
- ROC曲线:以 False Positive Rate 为横坐标,True Positive Rate 为纵坐标,绘制的曲线
- AUC(Area Under ROC Curve):ROC曲线下的面积
0.5 <= AUC <= 1.0
AUC曲线不受样本中真实值为正例和负例的比例影响,在样本标签不均衡的时候也具有可靠性。
F1会受样本标签正负比的影响。
AUC曲线只跟阈值threhold有关,随threhold的变化而变化
以上讨论的都是二分类问题,在多分类时,可以使用 OneVsRest 的策略,判断第 i 类的分类时,把不属于第 i 类的看做另一类,就能对每一类都算出一个 F1 值了。使用宏平均(macro)或者微平均(micro)来考量多分类的效果。宏平均是多个分类 F1 值相加,而微平均是多个 F1 分子分母分别相加。
macro-F1 = 1 N ∑ i N F i micro-F1 = 2 ∑ i N P i R i ∑ i N P i + R i \begin{aligned} \operatorname{macro-F1} &=\frac{1}{N} \sum_{i}^{N} F_{i} \\\operatorname{micro-F1} &=\frac{2 \sum_{i}^{N} P_{i} R_{i}}{\sum_{i}^{N} P_{i}+R_{i}} \end{aligned} macro-F1micro-F1=N1i∑NFi=∑iNPi+Ri2∑iNPiRi