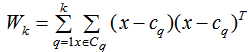【聚类】超详细的性能度量和相似度方法总结

目录

1. 外部指标

1.1 RI（兰德系数）

 1.2 ARI（调整兰德系数）

1.3 AMI（调整的互信息指数）

1.4 同质性，完整性和V-measure

1.5 Fowlkes-Mallows分数

2. 内部指标

2.1 轮廓系数（Silhouette Coefficient）

 2.2 Caliniski-Harabaz指数

 2.3 DB指数（Davies-Bouldin Index）

3. 相似度算法总结

3.1  距离计算

 3.2 余弦相似度计算

 3.3 线性核

 3.4 多项式核函数

3.5 Sigmoid核函数

 3.6 RBF核函数

3.7 拉普拉斯核函数

3.8 卡方核函数

---

非监督学习与监督学习最重要的区别在于训练数据是否包含标记数据，在机器学习开发的工作中，往往包含了大量的无标记数据和少量的标记数据，非监督方法通过对无标记训练样本的学习来发掘数据的内在规律，为进一步的数据分析提供基础。

聚类算法是非监督学习最常用的一种方法，性能度量是衡量学习模型优劣的指标，也可作为优化学习模型的目标函数。聚类性能度量根据训练数据是否包含标记数据分为两类，一类是将聚类结果与标记数据进行比较，称为“外部指标”；另一类是直接分析聚类结果，称为内部指标。本文对这两类的性能度量以及相似度方法作一个详细总结。

1. 外部指标

在详细介绍外部指标前，先定义两两配对变量a和b：

a：数据集的样本对既属于相同簇C也属于相同簇K的个数

b：数据集的样本对不属于相同簇C也不属于相同簇K的个数

用一个简单例子来说明a，b的含义：

真实簇向量：[ 0, 0, 0, 1, 1, 1 ]

预测簇向量：[ 0, 0, 1, 1, 2, 2 ]

a为属于相同簇向量的样本对个数，用红色框标记：

如上图：a = 2；

b为数据集不属于相同簇C也不属于相同簇K的样本对个数，用绿色框标记：

如上图：b = 1；

知道了a，b的含义，下面开始详细介绍外部指标的性能度量。

1.1 RI（兰德系数）

RI是衡量两个簇类的相似度，假设样本个数是n，定义：

其中

是所有可能的样本对个数。

假设：

真实簇向量：[ 0, 0, 0, 1, 1, 1 ]

预测簇向量：[ 0, 0, 1, 1, 2, 2 ]

RI系数的缺点是随着聚类数的增加，随机分配簇类向量的RI也逐渐增加，这是不符合理论的，随机分配簇类标记向量的RI应为0。

 1.2 ARI（调整兰德系数）

ARI解决了RI不能很好的描述随机分配簇类标记向量的相似度问题，ARI的定义：

其中E表示期望，max表示取最大值。

上式实现的具体公式：

其中 i，j分别为真实簇类和预测簇类，

表示真实簇类为i，预测簇类为j的个数，的含义与下表的相同，的含义与下表的相同。

用上面的例子来解释ARI的计算过程。

假设：

真实簇向量：[ 0, 0, 0, 1, 1, 1 ]

预测簇向量：[ 0, 0, 1, 1, 2, 2 ]

表格统计簇向量配对的个数：

因此，根据表格计算ARI指标：

由表格可知：

所以：ARI = 0.2424

from sklearn import metrics
# 真实的簇
labels_true = [0, 0, 0, 1, 1, 1]
# 预测的簇
labels_pred = [0, 0, 1, 1, 2, 2]
# 计算ARI
ARI = metrics.adjusted_rand_score(labels_true, labels_pred)
ARI

#> 0.24242424242424246

优点：

1）ARI的取值范围为[-1,1]，ARI越大表示预测簇向量和真实簇向量相似度越高，,ARI接近于0表示簇向量是随机分配，ARI为负数表示非常差的预测簇向量；

2）对于任意的簇类数和样本数，随机分配标签的ARI分数接近于0；

3）可用于评估无假设簇类结构的性能度量，如比较通过谱聚类降维后的k均值聚类算法的性能；

缺点：

需要知道真实数据的标记类信息，因此在实践中很难得到应用或可以人工手动标定数据（类似监督学习）；

1.3 AMI（调整的互信息指数）

AMI是基于预测簇向量与真实簇向量的互信息分数来衡量其相似度的，AMI越大相似度越高，AMI接近于0表示簇向量是随机分配的。MI（互信息指数）和NMI（标准化的互信息指数）不符合簇向量随机分配的理论，即随着分配簇的个数增加，MI和NMI亦会趋向于增加，AMI的值一直接近于0，因此采用AMI作为基于互信息的角度衡量簇向量间的相似度。由于篇幅原因，这里不再介绍具体的AMI计算公式，读者可参考scikit-learn官方网址的聚类章节。

AMI与MI的对比：

# AMI指数
AMI1 = metrics.adjusted_mutual_info_score(labels_true, labels_pred)
print('AMI= ',AMI)
# 若预测簇向量和真实簇向量完全相同
labes_pred = labels_true[:]
# 基于调整互信息指数分析的相似度应该为1
AMI2 = metrics.adjusted_mutual_info_score(labels_true, labes_pred)
print('AMI2= ',AMI2)
# 基于标准化互信息指数的相似度亦为1
NMI1 = metrics.normalized_mutual_info_score(labels_true, labes_pred)
print('NMI1= ',NMI1)
# 基于互信息指数的相似度不为1，不符合理论
MI = metrics.mutual_info_score(labels_true, labes_pred)
print('MI= ',MI)

#>
AMI1=  0.2250422831983088
AMI2=  1.0
NMI1=  1.0
MI=  0.6931471805599452

若簇向量是随机分配的，当簇类个数和样本数都较大时，MI和NMI的值不为0，ARI和AMI的值为0.

# 簇类个数
cluster_num = 100
# 样本个数
samples = 1000
# 分配函数
seed = 45
random_labels = np.random.RandomState(seed).randint
# 随机分配真实簇向量
labels_true = random_labels(low=0,high=cluster_num,size=samples)
# 随机分配预测簇向量
labels_pred = random_labels(low=0,high=cluster_num,size=samples)
# AMI计算相似度
AMI = metrics.adjusted_mutual_info_score(labels_true, labels_pred)
print('AMI= ',AMI)
# NMI计算相似度
NMI = metrics.normalized_mutual_info_score(labels_true, labels_pred)
print('NMI= ',NMI)
# MI计算相似度
MI = metrics.mutual_info_score(labels_true, labels_pred)
print('MI= ',MI)
# ARI计算相似度
ARI = metrics.adjusted_mutual_info_score(labels_true, labels_pred)
print('ARI= ',ARI)

#>
AMI=  0.006054902942529268   # 接近0
NMI=  0.5004078317894934
MI=  2.2775606710406766
ARI=  0.006054902942529268   # 接近0

优点：

1）对于任意的簇类数和样本数，随机分配标签的AMI分数接近于0。

2）有界范围[0,1]：0附近表示两个标签很大程度上是相互独立的，接近1表示一致的簇向量。

缺点：

1）这类指标需要知道真实数据的标记类信息，因此在实践中很难得到应用或可以人工手动标定数据（类似监督学习）

2）随机标签分配的NMI和MI不为0。

1.4 同质性，完整性和V-measure

同质性和完整性是基于条件熵的互信息分数来衡量簇向量间的相似度，V-meansure是同质性和完整性的调和平均。

同质性（homogeneity）：每个簇只包含单个类成员；

完整性（completeness）：给定类的所有成员分配给同一簇类；

同质性为1的情况：

# 同质性为1的情况
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 2, 2, 2]
homogeneity=metrics.homogeneity_score(labels_true, labels_pred)
print('homogeneity= ',homogeneity)

#>	homogeneity=  1.0

完整性为1的情况：

# 完整性为1的情况
labels_true = [0, 1, 1, 1, 2, 2]
labels_pred = [0, 0, 0, 0, 2, 2]
completeness=metrics.completeness_score(labels_true, labels_pred)
print('completeness= ',completeness)

#> completeness=  1.0

V-measure是结合同质性和完整性两个因素来评价簇向量间的相似度，V-measure为1表示最优的相似度：

# V-measure为1的情况
labels_true = [0, 0, 1, 1, 2, 2]
labels_pred = [1, 1, 2, 2, 3, 3]
completeness=metrics.v_measure_score(labels_true, labels_pred)
print('completeness= ',completeness)

#> completeness=  1.0

若V-measure值较小，我们可以从同质性和完整性方面给出定性的分析：

# V-measure的定性分析
labels_true =[0,0,0,1,1,1]
labels_pred =[0,0,0,1,2,3]
metrics.homogeneity_completeness_v_measure(labels_true,labels_pred)

# 顺序为：同质性，完整性和V-measure
#> (0.9999999999999997, 0.5578858913022595, 0.7162089270041652)

结果分析，V-measure值较小的原因是簇向量间的同质性较差。

优点：

1）有界的分数：0表示相似度最低，1表示相似度最高，分数与相似度成正相关的关系；

2）解释直观：对具有较差V-measure的聚类进行同质性和完整性的定性分析，明确聚类算法的错误类型；

3）对簇的结构没有作任何假设：如比较通过谱聚类降维后的k均值聚类算法的性能；

缺点：

1）随机标记没有标准化，因此随机标记不会总是产生相同的同质性、完整性和V-measure分数。特别是当簇类数量较大时，随机标记的V-meaure值不为0。

当样本数量大于1000簇类数量小于10时，这类问题可以忽略。对于更小的样本数量或更大的簇类数量，建议使用调整系数（比如ARI和AMI）。如下图，随着簇类个数的增加，随机标记的ARI和AMI值都接近于0，V-measure和mutual_info_score（互信息分数）逐渐增加；

 2）这类指标需要知道真实数据的标记类信息，因此在实践中很难得到应用或可以人工手动标定数据（类似监督学习）。

1.5 Fowlkes-Mallows分数

Fowlkes-Mallows指数（FMI）是成对准确率和召回率的几何平均值：

其中TP是真正例（True Positive），即真实标签和预测标签属于相同簇类的样本对个数；FP是假正例（False Positive），即真实标签属于同一簇类，相应的预测标签不属于该簇类的样本对个数；FN是假负例（False Negative），即预测标签属于同一簇类，相应的真实标签不属于该簇类的样本对个数。

假设真实簇向量：[ 0, 0, 0, 1, 1, 1 ]，预测簇向量：[ 0, 0, 1, 1, 2, 2 ]，求簇向量间的FMI.

根据定义可得：

TP = 2，FP=3，FN=1

因此：

代码表示：

 

# Fowlker-Mallows scores
labels_true =[0,0,0,1,1,1]
labels_pred =[0,0,1,1,2,2]
metrics.fowlkes_mallows_score(labels_true,labels_pred)

#>  0.4714045207910317

 优点：

1）对于任意的簇类数和样本数，随机簇类标签的FMI近似于0；

2）有界范围：FMI范围为[0,1]，值接近于0表示随机分配的标签在很大程度上是相互独立的，接近于1表示一致的簇向量；

3）对簇的结构没有作任何假设：可用来比较通过谱聚类降维后的k均值聚类算法的性能；

缺点：

1）这类指标需要知道真实数据的标记类信息，因此在实践中很难得到应用或可以人工手动标定数据（类似监督学习）。

2. 内部指标

如果数据集标签未知，则必须使用模型本身的内部指标去度量聚类性能。

下面对内部指标进行总结：

2.1 轮廓系数（Silhouette Coefficient）

每个样本有对应的轮廓系数，轮廓系数由两个得分组成：

• a：样本与同一簇类中的其他样本点的平均距离；

• b：样本与距离最近簇类中所有样本点的平均距离；

每个样本的轮廓系数定义为：

一组数据集的轮廓系数等于该数据集中每一个样本轮廓系数的平均值。

from sklearn import metrics
from sklearn.cluster import KMeans
from sklearn import datasets
# 生成数据集
dataset = datasets.load_iris()
X = dataset.data
y = dataset.target
# 构建K均值聚类模型
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
# 轮廓系数
metrics.silhouette_score(X, labels, metric='euclidean')

#> 0.5528190123564091

 优点：

1）轮廓系数处于[-1,1]的范围内，-1表示错误的聚类，1表示高密度的聚类，0附近表示重叠的聚类；

2）当簇密度较高且分离较大时，聚类的轮廓系数亦越大；

缺点：

1）凸簇的轮廓系数比其他类型的簇高，比如通过DBSCAN获得的基于密度的簇。

 2.2 Caliniski-Harabaz指数

评价聚类模型好的标准：同一簇类的数据集尽可能密集，不同簇类的数据集尽可能远离。

定义簇类散度矩阵

：

簇间散度矩阵

：

其中

为簇类q的样本集，为簇类q的中心，为簇类q的样本数，c为所有数据集的中心。

 根据协方差的相关概念，我们用簇类散度矩阵的迹表示同一簇类的密集程度，迹越小，同一簇类的数据集越密集（方差越小）；簇间散度矩阵的迹表示不同簇间的远离程度，迹越大，不同簇间的远离程度越大（方差越大）。

结合评价聚类模型的标准，定义Calinski-Harabaz指数：

其中N为数据集样本数，k为簇类个数，

，分别为簇间散度矩阵和簇类散度矩阵的迹。

# Caliniski-Harabaz指数
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
metrics.calinski_harabaz_score(X, labels)

#> 561.62775662962

优点：

1）当簇类密集且簇间分离较好时，Caliniski-Harabaz分数越高，聚类性能越好。

2）计算速度快。

缺点：

1）凸簇的Caliniski-Harabaz指数比其他类型的簇高，比如通过DBSCAN获得的基于密度的簇。

 2.3 DB指数（Davies-Bouldin Index）

我们用簇类C的平均距离表示该簇类的密集程度：

其中|C|表示簇类C的个数，dist(·,·)计算两个样本之间的距离。

 

不同簇类中心的距离表示不同簇类的远离程度：

其中

，分别为簇类和的中心。

结合聚类模型评价标准，定义DB指数：

DB指数的下限为0，DB指数越小，聚类性能越好。

优点：

1）DB指数的计算比轮廓系数简单；
2）DB指数的计算只需要知道数据集的数量和特征；

缺点：

1）凸簇的DB指数比其他类型的簇高，比如通过DBSCAN获得的基于密度的簇。

2）簇类中心的距离度量限制在欧式空间

至此，本节介绍了评价聚类性能特性的内部指标，内部指标是基于相似度展开的，若聚类结果的同一簇类的相似度好，不同簇间的相似度差，我们认为聚类性能较好。内部指标如轮廓系数和DB指数是基于样本间的距离来计算相似度，Calinski-Harabaz指数是基于协方差来计算相似度。下一节总结样本间的相似度算法。

3. 相似度算法总结

评价样本间相似度常用的方法是距离计算、余弦相似度计算和核函数计算，若样本间的距离越小，则相似度越高；若样本间的核函数值越大，则相似度越高。

距离和核函数的转换关系：

其中D是样本间的距离，gamma常取（1/features），S为映射的核。

下面总结了常用的相似度计算方法。

3.1  距离计算

给定样本

与，计算样本距离最常用方法的是“闵可夫斯基距离”（Minkowski distance）。

公式：

其中p≥1。

 p=2时，闵可夫斯基距离即欧氏距离（Euclidean distance）

# 欧式距离
import numpy as np
from sklearn.metrics import pairwise_distances
from sklearn.metrics.pairwise import pairwise_kernels
X = np.array([[2, 3]])
Y = np.array([[0, 1]])
pairwise_distances(X, Y, metric='euclidean')

#>
array([[2.82842712]])

p=1时，闵可夫斯基距离即曼哈顿距离（Manhattan distance）

 

#曼哈顿距离
pairwise_distances(X, Y, metric='manhattan')

#>
array([[4.]])

 3.2 余弦相似度计算

公式：

# 余弦相似度计算
pairwise_distances(X,Y,metric='cosine')

#>
array([[0.16794971]])

 3.3 线性核

# 线性核计算
pairwise_kernels(X,Y,metric='linear')

#>
array([[3.]])

 3.4 多项式核函数

# 多项式核计算
coef0 = 1
degress = 3
metrics.pairwise.polynomial_kernel(X, Y, degree=3,gamma=0.2,coef0=1)

#>
array([[4.096]])

3.5 Sigmoid核函数

# Sigmoid核函数
metrics.pairwise.sigmoid_kernel(X, Y,gamma=0.2,coef0=1)

#>
array([[0.92166855]])

 3.6 RBF核函数

# RBF核函数
metrics.pairwise.sigmoid_kernel(X, Y,gamma=0.2)

#>
array([[0.92166855]])

 

3.7 拉普拉斯核函数

# 拉普拉斯核函数
metrics.pairwise.laplacian_kernel(X, Y, gamma=0.2)

#>
array([[0.44932896]])

3.8 卡方核函数

# 卡方核函数
metrics.pairwise.chi2_kernel(X, Y, gamma=0.2)

#>
array([[0.54881164]])

 

---

参考

https://scikit-learn.org/stable/modules/metrics.html#metrics

https://scikit-learn.org/stable/modules/clustering.html#clustering

周志华 《机器学习》

---