Python图像处理八:图像频域滤波
一、图像频谱
在 numpy 库的 fft 模块中有计算二维离散傅里叶变换的函数 fft2,此外图像
变换到频域后,原点需要移动到频域矩形的中心,所以要对fft2的结果使用fftshift
函数实现频谱中心化。计算二维离散逆傅里叶变换的函数为 ifft2,频谱去中心化
的函数为 ifftshift。
输入一张灰度图,输出经过二维离散傅里叶变换后的结果,但是傅里叶变换
的结果为复数,需要通过使用 abs 函数求模才可以进行可视化,且因为傅里叶频
谱范围很大,所以要用对数变换来改善视觉效果。
在使用 log 函数的时候,要写成 log(1 + x) 而不是直接用 log(x),以避免出
现 x=0 的情况。
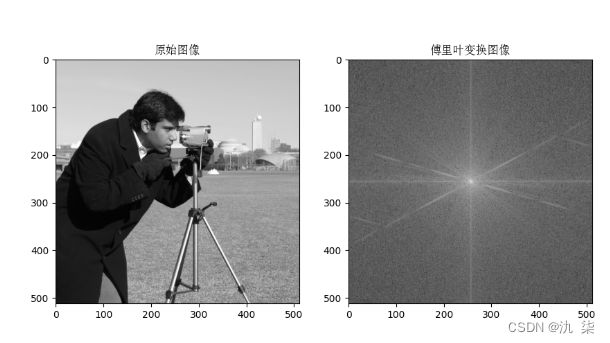
读入一幅灰度图像,求其频谱,代码示例如下:
from skimage import data
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.font_manager import FontProperties
font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
img = data.camera()
f = np.fft.fft2(img) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 将原点转移到中间位置
fimg = np.log(np.abs(fshift)+1) # fft 结果是复数,求模之后才是振幅
plt.figure(figsize=(10,10))
plt.subplot(121)
plt.imshow(img, 'gray')
plt.title('原始图像',fontproperties=font_set)
plt.subplot(122)
plt.imshow(fimg, 'gray')
plt.title('傅里叶变换图像',fontproperties=font_set)
plt.show()
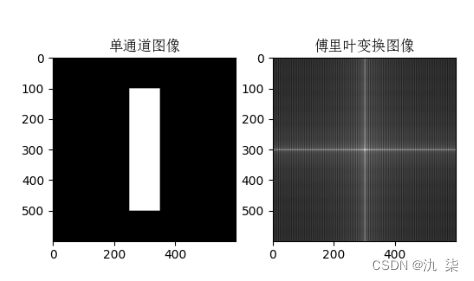
利用函数(np.zeros)生成一个 600* 600 的单通道图像,并在该图中心生成
一个高 400 宽 100 的白色矩形,得到亮块图像,求此图像的频谱图,代码示例如
下:
from skimage import data,transform
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.font_manager import FontProperties
font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
image=np.zeros((600,600),dtype='uint8')
image[100:500,250:350]=255
f=np.fft.fft2(image)
fshift = np.fft.fftshift(f)
fimg = np.log(np.abs(fshift)+1)
plt.figure(figsize=(6,8))
plt.subplot(121)
plt.imshow(image, plt.cm.gray)
plt.title('单通道图像',fontproperties=font_set)
plt.subplot(122)
plt.imshow(fimg, plt.cm.gray)
plt.title('傅里叶变换图像',fontproperties=font_set)
plt.show()
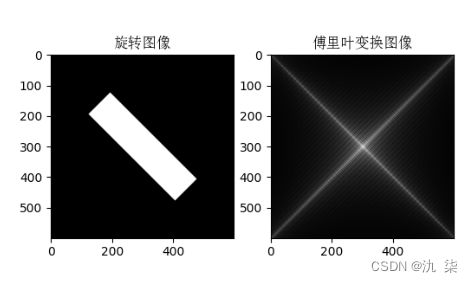
image2 =transform.rotate(image,45)
f=np.fft.fft2(image2)
fshift = np.fft.fftshift(f)
fimg = np.log(np.abs(fshift)+1)
plt.figure(figsize=(6,8))
plt.subplot(121)
plt.imshow(image2,plt.cm.gray)
plt.title('旋转图像',fontproperties=font_set)
plt.subplot(122)
plt.imshow(fimg,plt.cm.gray)
plt.title('傅里叶变换图像',fontproperties=font_set)
plt.show()
二、图像频域低通滤波
1. 理想低通滤波器
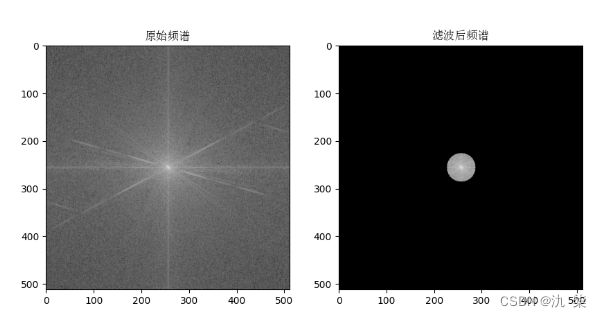
读入一幅灰度图像,用理想低通滤波器做滤波,代码示例如下:
from skimage import data
import numpy as np
from math import sqrt
from matplotlib import pyplot as plt
from matplotlib.font_manager import FontProperties
font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
img = data.camera()
f = np.fft.fft2(img) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 将原点转移到中间位置
fimg = np.log(np.abs(fshift)+1) # fft 结果是复数,求模之后才是振幅
#实现理想低通滤波器
D=30
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #计算频谱中心
mask=np.zeros((rows,cols),np.uint8) #生成 rows 行 cols 的矩阵,数据格式为 uint8
for i in range(rows):
for j in range(cols):
dis = sqrt((i - crow) ** 2 + (j - ccol) ** 2)
if dis <=D:# 将距离频谱中心小于 D 的部分低通信息 设置为 1,属于低通滤波
mask[i,j]=1
else:
mask[i,j]=0
f1_shift=fshift*mask
f_ishift=np.fft.ifftshift(f1_shift)
img_back=np.fft.ifft2(f_ishift)
img_back=np.abs(img_back)
plt.figure(figsize=(10,10))
plt.subplot(121)
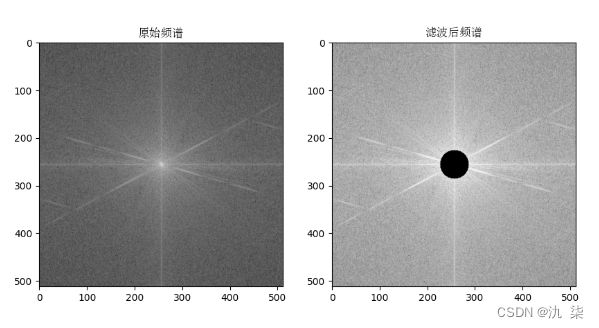
plt.imshow(fimg,plt.cm.gray)
plt.title('原始频谱',fontproperties=font_set)
plt.subplot(122)
plt.imshow(np.log(np.abs(f1_shift)+1),plt.cm.gray)
plt.title('滤波后频谱',fontproperties=font_set)
plt.figure(figsize=(10,10))
plt.subplot(121)
plt.imshow(img, plt.cm.gray)
plt.title('原始图像',fontproperties=font_set)
plt.subplot(122)
plt.imshow(img_back, plt.cm.gray)
plt.title('理想低通滤波后图像',fontproperties=font_set)
plt.show()
2. Butterworth 低通滤波器
读入一幅灰度图像,用 Butterworth 低通滤波器做滤波,代码示例如下:
from skimage import data
import numpy as np
from math import sqrt
from matplotlib import pyplot as plt
from matplotlib.font_manager import FontProperties
font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
img = data.camera()
f = np.fft.fft2(img) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 将原点转移到中间位置
transfor_matrix = np.zeros(img.shape)
#实现 Butterworth 低通滤波器
d=30
n=2
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #计算频谱中心
for i in range(rows):
for j in range(cols):
dis = sqrt((i - crow) ** 2 + (j - ccol) ** 2)
transfor_matrix[i, j] = 1 / (1 + (dis / d) ** (2*n))
f1_shift=fshift*transfor_matrix
f_ishift=np.fft.ifftshift(f1_shift)
img_back=np.fft.ifft2(f_ishift)
img_back=np.abs(img_back)
plt.figure(figsize=(10,10))
plt.subplot(121)
plt.imshow(img, plt.cm.gray)
plt.title('原始图像',fontproperties=font_set)
plt.subplot(122)
plt.imshow(img_back, plt.cm.gray)
plt.title('Butterworth 低通滤波后图像',fontproperties=font_set)
plt.show()
3. 高斯低通滤波器
读入一幅灰度图像,用高斯低通滤波器做滤波,代码示例如下:
from skimage import data
import numpy as np
from math import sqrt
from matplotlib import pyplot as plt
from matplotlib.font_manager import FontProperties
font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
img = data.camera()
f = np.fft.fft2(img) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 将原点转移到中间位置
transfor_matrix = np.zeros(img.shape)
#实现高斯低通滤波器
d=30
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #计算频谱中心
for i in range(rows):
for j in range(cols):
dis = sqrt((i - crow) ** 2 + (j - ccol) ** 2)
transfor_matrix[i, j] =np.exp(-dis ** 2/(2 * d ** 2))
f1_shift=fshift*transfor_matrix
f_ishift=np.fft.ifftshift(f1_shift)
img_back=np.fft.ifft2(f_ishift)
img_back=np.abs(img_back)
plt.figure(figsize=(10,10))
plt.subplot(121)
plt.imshow(img, plt.cm.gray)
plt.title('原始图像',fontproperties=font_set)
plt.subplot(122)
plt.imshow(img_back, plt.cm.gray)
plt.title('Gauss 低通滤波后图像',fontproperties=font_set)
plt.show()
三、图像频域高通滤波
1. 理想高通滤波器
读入一幅灰度图像,用理想高通滤波器做滤波,代码示例如下:
from skimage import data
import numpy as np
from math import sqrt
from matplotlib import pyplot as plt
from matplotlib.font_manager import FontProperties
font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
img = data.camera()
f = np.fft.fft2(img) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 将原点转移到中间位置
fimg = np.log(np.abs(fshift)+1) # fft 结果是复数,求模之后才是振幅
#实现理想高通滤波器
D=30
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #计算频谱中心
mask=np.zeros((rows,cols),np.uint8) #生成 rows 行 cols 的矩阵,数据格式为 uint8
for i in range(rows):
for j in range(cols):
dis = sqrt((i - crow) ** 2 + (j - ccol) ** 2)
if dis <=D:
# 将距离频谱中心大于 D 的部分高通信息设置为 1,属于高通滤波
mask[i,j]=0
else:
mask[i,j]=1
f1_shift=fshift*mask
f_ishift=np.fft.ifftshift(f1_shift)
img_back=np.fft.ifft2(f_ishift)
img_back=np.abs(img_back)
plt.figure(figsize=(10,10))
plt.subplot(121)
plt.imshow(fimg,plt.cm.gray)
plt.title('原始频谱',fontproperties=font_set)
plt.subplot(122)
plt.imshow(np.log(np.abs(f1_shift)+1),plt.cm.gray)
plt.title('滤波后频谱',fontproperties=font_set)
plt.figure(figsize=(10,10))
plt.subplot(121)
plt.imshow(img, plt.cm.gray)
plt.title('原始图像',fontproperties=font_set)
plt.subplot(122)
plt.imshow(img_back, plt.cm.gray)
plt.title('理想高通滤波后图像',fontproperties=font_set)
plt.show()
2. Butterworth 高通滤波器
读入一幅灰度图像,用 Butterworth 高通滤波器做滤波,代码示例如下:
from skimage import data
import numpy as np
from math import sqrt
from matplotlib import pyplot as plt
from matplotlib.font_manager import FontProperties
font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
img = data.camera()
f = np.fft.fft2(img) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 将原点转移到中间位置
transfor_matrix = np.zeros(img.shape)
#实现 Butterworth 高通滤波器
d=30
n=2
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #计算频谱中心
for i in range(rows):
for j in range(cols):
dis = sqrt((i - crow) ** 2 + (j - ccol) ** 2)
transfor_matrix[i, j] =1- 1 / (1 + (dis / d) ** (2*n))
f1_shift=fshift*transfor_matrix
f_ishift=np.fft.ifftshift(f1_shift)
img_back=np.fft.ifft2(f_ishift)
img_back=np.abs(img_back)
plt.figure(figsize=(10,10))
plt.subplot(121)
plt.imshow(img, plt.cm.gray)
plt.title('原始图像',fontproperties=font_set)
plt.subplot(122)
plt.imshow(img_back, plt.cm.gray)
plt.title('Butterworth 高通滤波后图像',fontproperties=font_set)
plt.show()
3. 高斯高通滤波器
读入一幅灰度图像,用高斯高通滤波器做滤波,代码示例如下:
from skimage import data
import numpy as np
from math import sqrt
from matplotlib import pyplot as plt
from matplotlib.font_manager import FontProperties
font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
img = data.camera()
f = np.fft.fft2(img) # 快速傅里叶变换算法得到频率分布
fshift = np.fft.fftshift(f) # 将原点转移到中间位置
transfor_matrix = np.zeros(img.shape)
#实现高斯高通滤波器
d=30
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #计算频谱中心
for i in range(rows):
for j in range(cols):
dis = sqrt((i - crow) ** 2 + (j - ccol) ** 2)
transfor_matrix[i, j] =1-np.exp(-dis ** 2/(2 * d ** 2))
f1_shift=fshift*transfor_matrix
f_ishift=np.fft.ifftshift(f1_shift)
img_back=np.fft.ifft2(f_ishift)
img_back=np.abs(img_back)
plt.figure(figsize=(10,10))
plt.subplot(121)
plt.imshow(img, plt.cm.gray)
plt.title('原始图像',fontproperties=font_set)
plt.subplot(122)
plt.imshow(img_back, plt.cm.gray)
plt.title('Gauss 高通滤波后图像',fontproperties=font_set)
plt.show()
每日“大饼”:
只要你想 这个世界就会有奇迹